step

Системный объект: phased.SumDifferenceMonopulseTracker2D
Пакет: поэтапный

Выполните отслеживание моноимпульса с помощью URA

Синтаксис

ESTANG = step(H,X,STANG)

Описание

Примечание

Запуск в R2016b, вместо того, чтобы использовать step метод, чтобы выполнить операцию, заданную Системой object™, можно вызвать объект с аргументами, как будто это была функция. Например, y = step(obj,x) и y = obj(x) выполните эквивалентные операции.

ESTANG = step(H,X,STANG) оценивает входящее направление ESTANG из входного сигнала, X, на основе исходного предположения направления.

Примечание

Объект выполняет инициализацию в первый раз, когда объект выполняется. Эта инициализация блокирует ненастраиваемые свойства и входные технические требования, такие как размерности, сложность и тип данных входных данных. Если вы изменяете ненастраиваемое свойство или входную спецификацию, Системный объект выдает ошибку. Чтобы изменить ненастраиваемые свойства или входные параметры, необходимо сначала вызвать release метод, чтобы разблокировать объект.

Входные параметры

H

Объект Tracker типа phased.SumDifferenceMonopulseTracker2D.

X

Входной сигнал в виде вектора-строки, количество которого столбцов соответствует количеству каналов. Можно задать этот аргумент как одинарную или двойную точность.

Размер первой размерности входной матрицы может варьироваться, чтобы симулировать изменяющуюся длину сигнала. Изменение размера может произойти, например, в случае импульсного сигнала с переменной импульсной частотой повторения.

STANG

Исходное предположение направления в виде 2 1 вектора в форме [AzimuthAngle; ElevationAngle] в градусах. Типичное исходное предположение является текущим руководящим углом. Углы азимута должны быть между –180 и 180. Углы возвышения должны быть между –90 и 90. Углы измеряются в системе локальной координаты массива. Для получения дополнительной информации относительно системы локальной координаты URA, введите phased.URA.coordinateSystemInfo. Можно задать этот аргумент как одинарную или двойную точность.

Выходные аргументы

ESTANG

Оценка входящего направления, возвращенного как 2 1 вектор в форме [AzimuthAngle; ElevationAngle] в градусах. Углы азимута между –180 и 180. Углы возвышения между –90 и 90. Углы измеряются в системе локальной координаты массива.

Примеры

развернуть все

Найдите целевое направление Используя различие суммы 2D моноимпульсным средством отслеживания

Скрипт Open Live Script

Используя URA, определите направление цели в азимуте на приблизительно 60 ° и вертикальном изменении на 20 °.

array = phased.URA('Size',4);
steeringvec = phased.SteeringVector('SensorArray',array);
tracker = phased.SumDifferenceMonopulseTracker2D('SensorArray',array);
x = steeringvec(tracker.OperatingFrequency,[60.1; 19.5]).';
est_dir = tracker(x,[60; 20])

est_dir = 2×1

   60.1000
   19.5000

Алгоритмы

Алгоритм моноимпульса суммы-и-различия используется к оценке направление прибытия узкополосного сигнала, посягающего на универсальную линейную матрицу (ULA). Во-первых, вычислите обычный ответ массива, управляемого к направлению прибытия φ ₀. Для ULA направление прибытия задано поперечным углом. Чтобы указать что точка максимальной оси ответа (MRA) к φ ₀ направлений, установите веса быть

$w_{s} = (1, e^{i k d \sin ϕ_{0}}, e^{i k 2 d \sin ϕ_{0}}, \dots, e^{i k (N - 1) d \sin ϕ_{0}})$

где d является интервалом элемента, и k = 2π/λ является wavenumber. Входящая плоская волна, прибывающая из любого произвольного направления φ, представлена

$v = (1, e^{i k d \sin ϕ}, e^{i k 2 d \sin ϕ}, \dots, e^{i k (N - 1) d \sin ϕ})$

Обычным ответом этого массива к любой входящей плоской волне дают $w_{s}^{H} v (φ)$ и показан в полярном графике ниже как Шаблон Суммы. Массив спроектирован, чтобы держаться к φ ₀ = 30 °.

Второй шаблон, названный Шаблоном Различия, получен при помощи поэтапно инвертированных весов. Веса определяются инвертированием фазы последняя половина обычного руководящего вектора. Для массива с четным числом элементов инвертированные фазой веса

$w_{d} = - i (1, e^{i k d \sin ϕ_{0}}, e^{i k 2 d \sin ϕ_{0}}, \dots, e^{i k N / 2 d \sin ϕ_{0}}, - e^{i k (N / 2 + 1) d \sin ϕ_{0}}, \dots, - e^{i k (N - 1) d \sin ϕ_{0}})$

(Для массива с нечетным числом элементов средний вес обнуляется). Мультипликативный факторный –i используется для удобства. Ответ массива различия к входящему вектору

$w_{d}^{H} v (φ)$

Этот рисунок показывает сумму, и диаграммы направленности различия четырехэлементной универсальной линейной матрицы (ULA) регулировали 30 ° от разворота. Элементы массива расположены с интервалами в половине длины волны. Шаблон суммы показывает, что массив имеет свой максимальный ответ на уровне 30 °, и шаблон различия имеет пустой указатель на уровне 30 °.

Моноимпульсная кривая отклика получена путем деления шаблона различия шаблоном суммы и принятия действительного участия.

$R (φ) = R e (\frac{w_{d}^{H} v (φ)}{w_{s}^{H} v (φ)})$

Чтобы использовать моноимпульсную кривую отклика, чтобы получить угол падения, φ, узкополосного сигнала, x, вычисляет

$z = R e (\frac{w_{d}^{H} x}{w_{s}^{H} x})$

и инвертируйте кривую отклика, ^{φ = R-1(z)}, чтобы получить φ.

Кривая отклика не обычно одна оцененный и может только быть инвертирована, когда углы падения лежат в основном лепестке, где это - один ценный Этот рисунок, показывает моноимпульсную кривую отклика в основном лепестке четырехэлементного массива ULA.

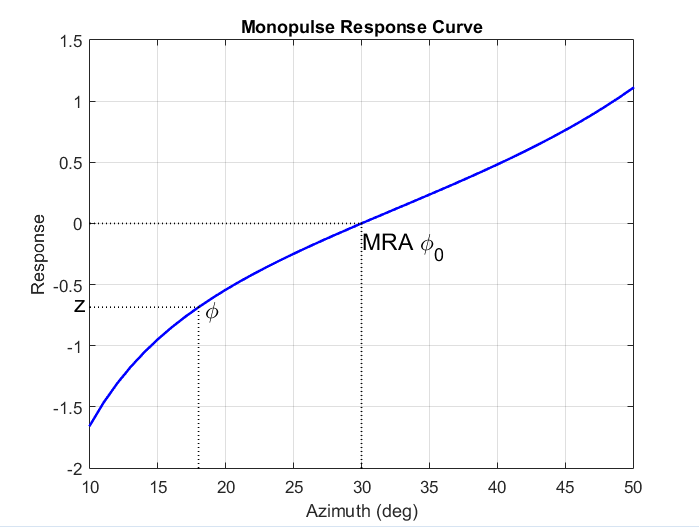
Существует два желательных свойства моноимпульсной кривой отклика. Прежде всего, это имеет крутой склон. Крутой склон обеспечивает робастность против шума. Второе свойство состоит в том, что mainlobe максимально широк. Крутой склон, убеждаются большим массивом, но приводит к меньшему mainlobe. Необходимо будет обменять одно свойство с другим.

Для получения дальнейшей информации см. [1].

Ссылки

[1] Seliktar, Y. Пространственно-временная адаптивная моноимпульсная обработка. Ph.D. Тезис. Технологический институт штата Джорджия, Атланта, 1998.

[2] Родос, D. Введение, чтобы монопульсировать. Дедхэм, MA: дом Artech, 1980.

Документация