Pipe (TL)

Закрытый кабелепровод для транспорта жидкости между тепловыми жидкими компонентами

Библиотека:
Simscape / Жидкости / Тепловая Жидкость / Pipes & Fittings

Описание

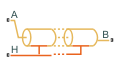
Модели блока Pipe (TL) тепловой жидкий поток через трубопровод. Температура через трубопровод вычисляется от температурного дифференциала между портами, вертикальным изменением трубопровода и любой дополнительной теплопередачей в порте H.

Трубопровод может иметь постоянное или различное вертикальное изменение между портами A и B. Для постоянного дифференциала вертикального изменения используйте параметр Elevation gain from port A to port B. Можно задать переменное вертикальное изменение установкой Elevation gain specification к Variable. Это отсоединяет порт EL физического сигнала.

Можно опционально смоделировать жидкую динамическую сжимаемость, инерцию и стенную гибкость. Когда эти явления моделируются, свойства потока вычисляются для каждого количества сегментов трубопровода, которые вы задаете.

Передайте гибкость по каналу

Гибкие стенки моделируются универсальным радиальным расширением, которое обеспечивает исходный трубопровод перекрестная частная форма. Можно определить площадь трубопровода в параметре Nominal cross-sectional area, подразумевая, что нет никакой заданной перекрестной частной геометрии, смоделированной блоком. Однако блок использует трубопровод гидравлический диаметр в вычислениях падения давления и теплопередаче.

Деформация диаметра трубопровода вычисляется как:

$\dot{D} = \frac{D_{S} - D}{τ},$

где:

_DS является постдеформацией, установившимся диаметром трубопровода,

$D_{S} = D_{N} + K_{c} (p - p_{a t m}),$
где K _c является Static pressure-diameter compliance, p является давлением трубы, и _patm является атмосферным давлением. Принимая эластичную деформацию тонкостенного, открытого трубопровода, можно вычислить K _c как:

$K_{c} = \frac{D^{2}}{2 t E},$
где t является толщиной стенок трубопровода, и E является модулем Янга.
_DN является номинальным диаметром трубопровода или диаметром до деформации:

$D_{N} = \sqrt{\frac{4 S}{π}},$
где S является Nominal cross-sectional area трубопровода.
D является трубопроводом Hydraulic diameter.
τ является Viscoelastic pressure time constant.

Теплопередача в стенке трубопровода

Можно смоделировать теплопередачу к и от стенок трубопровода несколькими способами. Существует две аналитических модели: Gnielinski correlation, который моделирует номер Nusselt в зависимости от Рейнольдса и чисел Прандтля с предопределенными коэффициентами и Dittus-Boelter correlation - Nusselt = a*Re^b*Pr^c, который моделирует номер Nusselt в зависимости от Рейнольдса и чисел Прандтля с пользовательскими коэффициентами.

Nominal temperature differential vs. nominal mass flow rate, Tabulated data - Colburn factor vs. Reynolds number, и Tabulated data - Nusselt number vs. Reynolds number & Prandtl number параметризация интерполяционной таблицы на основе предоставленных пользователями данных.

Теплопередача между жидкостью и стенкой трубопровода происходит посредством конвекции, Q _Conv и проводимость, _Cond Q.

Теплопередача из-за проводимости:

$Q_{Cond} = \frac{k_{I} S_{H}}{D} (T_{H} - T_{I}),$

где:

D является Hydraulic diameter, если стенки трубопровода тверды, и трубопровод установившийся диаметр, _DS, если стенки трубопровода гибки.
_kI является теплопроводностью тепловой жидкости, заданной внутренне для каждого сегмента трубопровода.
_SH является площадью поверхности стенки трубопровода.
_TH является температурой трубопровода стенки.
_TI является температурой жидкости, взятой в трубопроводе внутренний узел.

Теплопередача из-за конвекции:

$Q_{Conv} = c_{p,Avg} | {\dot{m}}_{Avg} | (T_{H} - T_{In}) [1 - exp (- \frac{h S_{H}}{c_{p,Avg} | {\dot{m}}_{Avg} |})],$

где:

c _{p, В среднем} средняя жидкая удельная теплоемкость.
$\dot{m}$ _{В среднем} средний массовый расход жидкости через трубопровод.
_TIn является жидкой входной температурой порта.
h является коэффициентом теплопередачи трубопровода.

Коэффициент теплопередачи h:

$h = \frac{Nu k_{Avg}}{D},$

кроме тех случаев, когда параметризация Nominal temperature differential vs. nominal mass flow rate, где _kAvg является средней теплопроводностью тепловой жидкости по целому трубопроводу, и Nu является средним номером Nusselt в трубопроводе.

Параметризация Analytical

Когда Heat transfer parameterization установлен в Gnielinski correlation и поток турбулентен, средний номер Nusselt вычисляется как:

$Nu = \frac{\frac{f}{8} (Re - 1000) PR}{1 + 12.7 {(\frac{f}{8})}^{1 / 2} ({Pr}^{2/3} - 1)},$

где:

f является средним значением коэффициент трения Дарси, согласно корреляции Haaland:

$f = {- 1.8 {log}_{10} [\frac{6.9}{Ре} + {(\frac{ϵ_{R}}{3.7 D})}^{1.11}]}^{-2},$
где ε _R является трубопроводом Internal surface absolute roughness.
Re является числом Рейнольдса.
Pr является числом Прандтля.

Когда поток ламинарен, номер Nusselt является параметром Nusselt number for laminar flow heat transfer.

Когда Heat transfer parameterization установлен в Dittus-Boelter correlation и поток турбулентен, средний номер Nusselt вычисляется как:

$Nu = a {Ре}_{}^{b} {PR}_{}^{c},$

где:

a является значением параметра Coefficient a.
b является значением параметра Exponent b.
c является значением параметра Exponent c.

Корреляция Диттуса-Болтера значения по умолчанию блока:

$Nu = 0.023 {Ре}_{}^{0.8} {PR}_{}^{0.4} .$

Когда поток ламинарен, номер Nusselt является параметром Nusselt number for laminar flow heat transfer.

Параметризация табличными данными

Когда Heat transfer parameterization установлен в Tabulated data - Colburn factor vs. Reynolds number, средний номер Nusselt вычисляется как:

$Nu = J_{M} (Ре) {RePr}_{}^{1 / 3} .$

где J _M является коэффициентом Колборна-Чилтона.

Когда Heat transfer parameterization установлен в Tabulated data - Nusselt number vs. Reynolds number & Prandtl number, номер Nusselt интерполирован от 3D массива avergae номера Nusselt и в зависимости от среднего числа Рейнольдса и в зависимости от среднего числа Прандтля:

$Nu = \nu (Ре, PR) .$

Когда Heat transfer parameterization установлен в Nominal temperature difference vs. nominal mass flow rate и поток турбулентен, коэффициент теплопередачи вычисляется как:

$h = \frac{h_{N} D_{N}^{1.8}}{{\dot{m}}_{N}^{0.8}} \frac{{\dot{m}}_{В среднем}^{0.8}}{D^{1.8}},$

где:

$\dot{m}$ _N является Nominal mass flow rate.
$\dot{m}$ _{В среднем} средний массовый расход жидкости:

${\dot{m}}_{A v g} = \frac{{\dot{m}}_{A} + {\dot{m}}_{B}}{2} .$
h _N является номинальным коэффициентом теплопередачи, который вычисляется как:

$h_{N} = \frac{{\dot{m}}_{N} c_{p,N}}{S_{H,N}} ln (\frac{T_{H,N} - T_{In, N}}{T_{H,N} - T_{Out,N}}),$
где:
- _SH,N является номинальной стенной площадью поверхности.
- _TH,N является Nominal wall temperature.
- _TIn,N является Nominal inflow temperature.
- _TOut,N является Nominal outflow temperature.

Это отношение основано на предположении, что номер Nusselt пропорционален числу Рейнольдса:

$\frac{h D}{k} \propto {(\frac{\dot{m} D}{S μ})}^{0.8} .$

Если стенки трубопровода тверды, выражение для коэффициента теплопередачи становится:

$h = \frac{h_{N}}{{\dot{m}}_{N}^{0.8}} {\dot{m}}_{A v g}^{0.8} .$

Падение давления из-за вязкого трения

Существует несколько способов смоделировать перепад давления по трубопроводу. Haaland correlation предоставляет аналитическую модель для потоков через круглые сечения с коэффициентом трения Дарси. Nominal pressure drop vs. nominal mass flow rate и Tabulated data - Darcy friction factor vs. Reynolds number параметризация позволяет вам обеспечивать данные, которые блок будет использовать в качестве интерполяционной таблицы в процессе моделирования.

Параметризация Analytical

Когда Viscous friction parameterization установлен в Haaland correlation и поток турбулентен, падение давления на трение в стенках трубопровода определяется уравнением Darcy-Weisbach:

$p_{A} - p_{I} = f \frac{{\dot{m}}_{A} | {\dot{m}}_{A} |}{2 ρ_{I} D S^{2}} (\frac{L + L_{Add}}{2}),$

где:

L является Pipe length.
_LE является Aggregate equivalent length of local resistances, который является эквивалентной длиной трубы, которая вводит ту же сумму потери как сумма потерь из-за других локальных сопротивлений в трубе.

Перепад давления между портом B и внутренним узлом я:

$p_{B} - p_{I} = f \frac{{\dot{m}}_{B} | {\dot{m}}_{B} |}{2 ρ_{I} D S^{2}} (\frac{L + L_{Add}}{2}),$

Когда поток ламинарен, падение давления на трение вычисляется в терминах Laminar friction constant for Darcy friction factor, λ. Перепад давления между портом A и внутренним узлом я:

$p_{A} - p_{I} = \frac{λ μ {\dot{m}}_{A}}{2 ρ D^{2} S} (\frac{L + L_{Add}}{2}) .$

Перепад давления между портом B и внутренним узлом я:

$p_{B} - p_{I} = \frac{λ μ {\dot{m}}_{B}}{2 ρ D^{2} S} (\frac{L + L_{Add}}{2}) .$

Для переходных потоков перепад давления из-за вязкого трения является сглаживавшим смешением между значениями для ламинарного и турбулентного падения давления.

Параметризация табличными данными

Когда Viscous friction parameterization установлен в Nominal pressure drop vs. nominal mass flow rate, падение давления из-за вязкого трения вычисляется по двум половинам трубопровода с коэффициентом потерь _Kp:

$Δ p_{f, A} = \frac{1}{2} K_{p} {\dot{m}}_{A} \sqrt{{\dot{m}}_{A}^{2} + {\dot{m}}_{Th}^{2}}$

$Δ p_{f, B} = \frac{1}{2} K_{p} {\dot{m}}_{B} \sqrt{{\dot{m}}_{B}^{2} + {\dot{m}}_{Th}^{2}}$

где:

${\dot{m}}_{Th}$ Mass flow rate threshold for flow reversal.
K _p является коэффициентом падения давления. Для стенок шланга коэффициент падения давления:

$K_{p} = \frac{p_{N}}{{\dot{m}}_{N}^{2}} D_{N},$
где:
- _pN является Nominal pressure drop.
- $\dot{m}$ _N является Nominal mass flow rate.
Коэффициент падения давления

$K_{p} = \frac{p_{N}}{{\dot{m}}_{N}^{2}},$
когда стенки трубопровода тверды. Когда Nominal pressure drop и параметры Nominal mass flow rate являются векторами, значение _Kp определяется как метод наименьших квадратов векторных элементов.

Когда

Когда Viscous friction parameterization установлен в Tabulated data – Darcy friction factor vs. Reynolds number, коэффициент трения интерполирован от табличных данных в зависимости от числа Рейнольдса:

$f = f (Re) .$

Баланс импульса

Перепад давления по трубопроводу происходит из-за давления в портах трубопровода, трения в стенках трубопровода и гидростатических изменений из-за любой разницы в вертикальном положении:

$p_{A} - p_{B} = Δ p_{f} + ρ_{I} g Δ z,$

где:

_pA является давлением в порте A.
_pB является давлением в порте B.
_Δpf является перепадом давления из-за вязкого трения, _{Δpf,A+Δpf,B}.
g является Gravitational acceleration.
Δz дифференциал вертикального изменения между портом A и портом B или _{zA - zB}.
_ρI является внутренней плотностью жидкости, которая измеряется в каждом сегменте трубопровода. Если жидкая динамическая сжимаемость не моделируется, это:

$p_{I} = \frac{p_{A} + p_{B}}{2} .$

Когда инерция жидкости не моделируется, баланс импульса между портом A и внутренним узлом, я:

$p_{A} - p_{I} = Δ p_{f, A} + ρ_{I} g \frac{Δ z}{2} .$

Когда инерция жидкости не моделируется, баланс импульса между портом B и внутренним узлом, я:

$p_{B} - p_{I} = Δ p_{f, B} - ρ_{I} g \frac{Δ z}{2} .$

Когда инерция жидкости моделируется, баланс импульса между портом A и внутренним узлом, я:

$p_{A} - p_{I} = Δ p_{f, A} + ρ_{I} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{A}}{S} \frac{L}{2},$

где:

$\ddot{m}$ _A является инерцией жидкости в порте A.
L является Pipe length.
S является Nominal cross-sectional area.

Когда инерция жидкости моделируется, баланс импульса между портом B и внутренним узлом, я:

$p_{B} - p_{I} = Δ p_{f, B} - ρ_{I} g \frac{Δ z}{2} + \frac{{\ddot{m}}_{B}}{S} \frac{L}{2},$

где

$\ddot{m}$ _B является инерцией жидкости в порте B.

Передайте дискретизацию по каналу

Можно разделить трубопровод на несколько сегментов. Если трубопровод имеет больше чем один сегмент, массовый поток, энергетический поток, и уравнения баланса импульса вычисляются для каждого сегмента. Наличие нескольких сегментов трубопровода может позволить вам отслеживать изменения к переменным, таким как плотность жидкости, когда жидкая динамическая сжимаемость моделируется.

Если требуется получить определенные явления в приложении, такие как гидравлический удар, выбрать много сегментов, который обеспечивает достаточное разрешение переходного процесса. Следующая формула, от теоремы отсчетов Найквиста, обеспечивает эмпирическое правило для дискретизации трубопровода в минимум сегментов N:

$N = 2 L \frac{f}{c},$

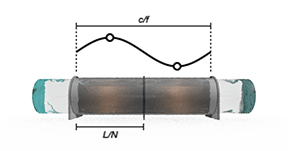
где:

L является Pipe length.
f является переходной частотой.
c является скоростью звука.

В некоторых случаях, такие как моделирование тепловых переходных процессов вдоль трубопровода, это может лучше подходить для вашего приложения, чтобы соединить несколько блоков Pipe (TL) последовательно.

Баланс массы

Для твердого трубопровода с несжимаемой жидкостью уравнение разговора массы трубопровода:

${\dot{m}}_{A} + {\dot{m}}_{B} = 0,$

где:

$\dot{m}$ _A является массовым расходом жидкости в порте A.
$\dot{m}$ _B является массовым расходом жидкости в порте B.

Для шланга с несжимаемой жидкостью уравнение сохранения массы трубопровода:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{I} \dot{V},$

где:

_ρI является тепловой жидкой плотностью во внутреннем узле I. Каждый сегмент трубопровода имеет внутренний узел.
$\dot{V}$ уровень деформации объема трубопровода.

Для шланга со сжимаемой жидкостью уравнение сохранения массы трубопровода: Эта зависимость получена модулем объемной упругости и тепловым коэффициентом расширения тепловой жидкости:

${\dot{m}}_{A} + {\dot{m}}_{B} = ρ_{I} \dot{V} + ρ_{I} V (\frac{{\dot{p}}_{I}}{β_{I}} - α_{I} {\dot{T}}_{I}),$

где:

_pI является тепловым жидким давлением во внутреннем узле I.
$\dot{T}$ _Я - скорость изменения тепловой жидкой температуры во внутреннем узле I.
_βI является тепловым жидким модулем объемной упругости.
α является жидким тепловым коэффициентом расширения.

Энергетический баланс

Энергетическая скорость накопления в трубопроводе во внутреннем узле я задан как:

$\dot{E} = ϕ_{A} + ϕ_{B} + ϕ_{H} - {\dot{m}}_{A v g} g Δ z,$

где:

_ϕA является энергетической скоростью потока жидкости в порте A.
_ϕB является энергетической скоростью потока жидкости в порте B.
_ϕH является энергетической скоростью потока жидкости в порте H.

Полная энергия задана как:

$E = ρ_{I} u_{I} V,$

где:

_uI является жидкой определенной внутренней энергией в узле I.
V является объемом трубопровода.

Если жидкость сжимаема, выражение для энергетической скорости накопления:

$\dot{E} = ρ_{I} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{I} .$

Если жидкость сжимаема, и стенки трубопровода гибки, выражение для энергетической скорости накопления:

$\dot{E} = ρ_{I} V {(\frac{d u}{d p} \frac{d p}{d t} + \frac{d u}{d T} \frac{d T}{d t})}_{I} + (ρ_{I} u_{I} + p_{I}) {(\frac{d V}{d t})}_{I} .$

Порты

Входной параметр

развернуть все

`EL` — Различие в вертикальном изменении порта
физический сигнал

Переменный дифференциал вертикального изменения между портом A и B в виде физического сигнала.

Сохранение

развернуть все

`A` — Открытие трубопровода
тепловая жидкость

Жидкая запись или выходной порт к трубопроводу.

`B` — Открытие трубопровода
тепловая жидкость

Жидкая запись или выходной порт к трубопроводу.

`H` — Передайте стенку по каналу
тепловой

Передайте температуру стенки по каналу.

Параметры

развернуть все

Настройка

`Fluid dynamic compressibility` — Смоделировать ли жидкую динамическую сжимаемость
`On` (значение по умолчанию) | `Off`

Смоделировать ли какое-либо изменение в плотности жидкости из-за сжимаемости жидкости. Когда Fluid compressibility установлен в On, изменения из-за массового расхода жидкости в блок вычисляются в дополнение к изменениям плотности из-за изменений в давлении.

`Fluid inertia` — Ли к ускорению жидкости модели
`On` (значение по умолчанию) | `Off`

Ли с учетом ускорения в массовом расходе жидкости из-за массы жидкости.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility на On.

`Number of segments` — Передайте дискретизацию по каналу
1 (значение по умолчанию) | положительный безразмерный скаляр

Количество делений трубопровода. Каждое деление представляет отдельный сегмент, по которому давление вычисляется, в зависимости от входного давления трубопровода, сжимаемости жидкости и стенной гибкости, если применимо. Объем жидкости в каждом сегменте остается фиксированным.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility на On.

`Pipe total length` — Общая длина трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Общая длина трубопровода через все сегменты трубопровода.

`Nominal cross-sectional area` — Перекрестная частная область трубопровода без деформации
0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

Площадь поперечного сечения трубопровода без деформаций.

`Pipe wall specification` — Задает стенную гибкость
`Rigid` (значение по умолчанию) | `Flexible`

Задает стенки трубопровода как твердые или гибкие. Гибкие стенки моделируются универсальным радиальным расширением, которое обеспечивает исходный трубопровод перекрестная частная форма.

Зависимости

Чтобы включить этот параметр, установите Fluid dynamic compressibility на On.

`Hydraulic diameter` — Эффективный диаметр некруглых сечений
`0.1128 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Эффективный диаметр используется в теплопередаче, балансе импульса и уравнениях гибкости трубопровода. Для некруглых сечений гидравлический диаметр является эффективным диаметром жидкости в трубопроводе. Для круглых сечений гидравлический диаметр и диаметр трубопровода являются тем же самым.

Зависимости

Чтобы включить этот параметр, установите также:

Fluid dynamic compressibility к Off.
Pipe wall specification к Rigid и Fluid dynamic compressibility к On.

`Elevation gain specification` — Установите свойство вертикального изменения трубопровода
`Constant` (значение по умолчанию) | `Variable`

Установите вертикальное изменение трубопровода как любой Constant или Variable. Выбор Variable отсоединяет порт EL физического сигнала.

`Elevation gain from port A to port B` — Разница в вертикальном положении на порте A относительно порта B
`0 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Дифференциал вертикального изменения для трубопроводов постоянного вертикального изменения. Усиление вертикального изменения должно быть меньше чем или равно общей длине Трубопровода.

Зависимости

Чтобы включить этот параметр, установите Elevation gain specification на Constant.

`Gravitational acceleration` — Ускорение из-за силы тяжести при среднем вертикальном изменении трубопровода
`9.81 m/s^2` (значение по умолчанию) | положительная скалярная величина в модулях length/time^2

Постоянный из гравитационного ускорения (g) при среднем вертикальном изменении трубопровода.

`Static pressure-diameter compliance` — Мера деформации трубопровода
`1.2e-6 m/MPa` (значение по умолчанию) | положительная скалярная величина в единицах длины/давления

Коэффициент трубопровода радиальная деформация из-за изменений в давлении. Это - материальная собственность трубопровода.

Зависимости

Чтобы включить этот параметр, установите Pipe wall specification на Flexible.

`Viscoelastic process time constant` — Передайте постоянную времени деформации по каналу
`0.01 s` (значение по умолчанию) | положительная скалярная величина в модулях времени

Время, требуемое для стенки достигнуть установившийся после деформации трубопровода. Этот параметр влияет на динамическое изменение в объеме трубопровода.

Зависимости

Чтобы включить этот параметр, установите Pipe wall specification на Flexible.

Вязкое трение

`Viscous friction parameterization` — Модель Friction
`Haaland correlation` (значение по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

Параметризация падения давления из-за стенного трения. И аналитические и табличные формулировки доступны.

`Aggregate equivalent length of local resistances` — Незначительное падение давления в трубопроводе, описанном как длина
`1 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Длина трубопровода, который произвел бы эквивалентные гидравлические потери, как будет трубопровод с поворотами, изменениями области или другим nonuniformies. Эффективная длина трубопровода является суммой длины Трубопровода и Совокупная эквивалентная продолжительность локальных сопротивлений.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Haaland correlation.

`Internal surface absolute roughness` — Передайте стенку по каналу абсолютная шероховатость
`1.5e-5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

Передайте стенку по каналу абсолютная шероховатость. Этот параметр используется, чтобы определить коэффициент трения Дарси, который способствует падению давления в трубопроводе.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Haaland correlation.

`Shape factor for laminar flow viscous friction` — Трение, постоянное для ламинарных течений
64 (значение по умолчанию) | положительный безразмерный скаляр

Трение, постоянное для ламинарных течений. Коэффициент трения Дарси получает вклад стенного трения в вычислениях падения давления.

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, ниже которого поток ламинарен. Выше этого порога, переходов потока к турбулентному, достигая турбулентного режима при установке Turbulent flow lower Reynolds number limit.

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

Число Рейнольдса, выше которого поток турбулентен. Ниже этого порога, поток постепенно переходы к ламинарному, достигая ламинарного режима при установке Laminar flow upper Reynolds number limit.

`Nominal mass flow rate` — Передайте массовый расход жидкости по каналу
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

Передайте по каналу номинальный массовый расход жидкости, используемый, чтобы вычислить коэффициент падения давления в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как параметр Nominal pressure drop. Когда этот параметр предоставляется как вектор, скалярное значение, Kp определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Nominal pressure drop vs. nominal mass flow rate.

`Nominal pressure drop` — Перепад давления по трубопроводу
`[0.001 0.01] MPa` (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

Передайте по каналу номинальный перепад давления, используемый, чтобы вычислить коэффициент падения давления в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр массового расхода жидкости. Когда этот параметр предоставляется как вектор, скалярное значение, Kp определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Nominal pressure drop vs. nominal mass flow rate.

`Mass flow rate threshold for flow reversal` — Порог, ниже которого применяется числовое сглаживание
`1e-6 kg/s` (значение по умолчанию) | положительная скалярная величина в единицах массы/времени

Порог массового расхода жидкости для обратного потока. Область перехода задана приблизительно 0 кг/с между положительными и отрицательными величинами порога массового расхода жидкости. В этой области перехода числовое сглаживание применяется к ответу потока. Пороговое значение должно быть больше 0.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Nominal pressure drop vs. nominal mass flow rate.

`Reynolds number vector for turbulent Darcy friction factor` — Числа Рейнольдса, в которых можно свести в таблицу коэффициент трения Дарси
`[ 400 1000 1.5e+3 3e+3 4e+3 6e+3 1e+4 2e+4 4e+4 6e+4 1e+5 1e+8 ]` (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из чисел Рейнольдса для табличной параметризации коэффициента трения Дарси. Векторные элементы формируют независимую ось параметром вектора коэффициента трения Дарси. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Для обратных потоков, или течет из B к A, те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Tabulated data - Darcy friction factor vs. Reynolds number.

`Darcy friction factor vector` — Коэффициенты трения дарси в сведенных в таблицу числах Рейнольдса
[ 0.264 0.112 0.07099999999999999 0.0417 0.0387 0.0268 0.025 0.0232 0.0226 0.022 0.0214 0.0214 ] (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из коэффициентов трения Дарси для табличной параметризации коэффициента трения Дарси. Векторные элементы должны соответствовать непосредственные элементам в векторе числа Рейнольдса для турбулентного параметра коэффициента трения Дарси, и должны быть уникальными и больше, чем или равными 0.

Зависимости

Чтобы включить этот параметр, установите Viscous friction parameterization на Tabulated data - Darcy friction factor vs. Reynolds number.

Теплопередача

`Heat transfer parameterization` — Метод, которым можно получить конвективную теплопередачу со стенкой трубопровода
`Gnielinski correlationNominal temperature differential vs. nominal mass flow rate` (значение по умолчанию) | `Dittus-Boelter correlation` | `Tabulated data - Colburn factor vs. Reynolds number` | `Tabulated data - Nusselt number vs. Reynolds number & Prandtl number`

Метод вычисления коэффициента теплопередачи между жидкостью и стенкой трубопровода. Аналитичный и параметризация табличных данных доступны.

`Nusselt number for laminar flow heat transfer` — Номер Nusselt, чтобы использовать в вычислениях теплопередачи для ламинарных течений
3.66 (значение по умолчанию)

Отношение конвективных к проводящей теплопередаче в ламинарном режиме течения жидкости. Жидкий номер Nusselt влияет на уровень теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на также:

Gnielinski correlation.
Nominal temperature differential vs. nominal mass flow rate.
Dittus-Boelter correlation.

`Nominal mass flow rate` — Передайте массовый расход жидкости по каналу
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

Передайте по каналу номинальный массовый расход жидкости, используемый, чтобы вычислить коэффициент теплопередачи в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр температуры притока. Когда этот параметр предоставляется как вектор, скалярное значение, h _p определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow temperature` — Передайте входную температуру по каналу
`[293.15 293.15] K` (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Номинальная жидкая входная температура раньше вычисляла коэффициент теплопередачи в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр массового расхода жидкости. Когда этот параметр предоставляется как вектор, скалярное значение, h определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Nominal temperature differential vs. nominal mass flow rate.

`Nominal outflow temperature` — Передайте выходную температуру по каналу
`[300 300] K`'(значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Номинальная жидкая выходная температура раньше вычисляла коэффициент теплопередачи в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр массового расхода жидкости. Когда этот параметр предоставляется как вектор, скалярное значение, h определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Nominal temperature differential vs. nominal mass flow rate.

`Nominal inflow pressure` — Передайте входное давление по каналу
`[0.101325 0.101325] MPa` (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

Номинальное жидкое входное давление раньше вычисляло коэффициент теплопередачи в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр массового расхода жидкости. Когда этот параметр предоставляется как вектор, скалярное значение, h определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Nominal temperature differential vs. nominal mass flow rate.

`Nominal wall temperature` — Передайте температуру стенки по каналу
`[303.15 303.15] K` (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Передайте по каналу температуру стенки, используемую, чтобы вычислить коэффициент теплопередачи в виде скаляра или вектора. Вся номинальная стоимость должна быть больше 0 и иметь то же число элементов как Номинальный параметр массового расхода жидкости. Когда этот параметр предоставляется как вектор, скалярное значение, h определяется как метод наименьших квадратов векторных элементов.

Зависимости

Чтобы включить эту температуру, установите Heat transfer parameterization на Nominal temperature differential vs. nominal mass flow rate.

`Coefficient a` — Эмпирический постоянный a корреляции Диттуса-Болтера
0.023 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирический постоянный a, чтобы использовать в корреляции Диттуса-Болтера. Корреляция связывает номер Nusselt в турбулентных течениях к коэффициенту теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Dittus-Boelter correlation.

`Exponent b` — Эмпирический постоянный b корреляции Диттуса-Болтера
0.8 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирический постоянный b, чтобы использовать в корреляции Диттуса-Болтера. Корреляция связывает номер Nusselt в турбулентных течениях к коэффициенту теплопередачи.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Dittus-Boelter correlation.

`Exponent c` — Эмпирический постоянный c корреляции Диттуса-Болтера
0.4 (значение по умолчанию) | положительный безразмерный скаляр

Эмпирический постоянный c, чтобы использовать в корреляции Диттуса-Болтера. Корреляция связывает номер Nusselt в турбулентных течениях к коэффициенту теплопередачи. Значение по умолчанию отражает теплопередачу к жидкости.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Dittus-Boelter correlation.

`Reynolds number vector for Colburn factor` — Числа Рейнольдса, в которых можно свести в таблицу коэффициент Колборна
[100 150 1000] (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из чисел Рейнольдса для табличной параметризации коэффициента Колборна. Векторные элементы формируют независимую ось параметром вектора коэффициента Колборна. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0. Этот параметр должен иметь то же число элементов как вектор коэффициента Колборна. Для обратных потоков, или течет из B к A, те же данные применяются в противоположном направлении.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Tabulated data - Colburn factor vs. Reynolds number.

`Colburn factor vector` — Коэффициенты Колборна, в который сведенные в таблицу числа Рейнольдса
[0.019 0.013 0.002] (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из факторов Colbrun для табличной параметризации коэффициента Колборна. Векторные элементы формируют независимую ось с вектором числа Рейнольдса для параметра коэффициента Колборна. Этот параметр должен иметь то же число элементов как вектор числа Рейнольдса для коэффициента Колборна.

Зависимости

Этот параметр активен, когда параметры блоков Heat transfer parameterization установлены в Tabulated data - Colburn factor vs. Reynolds number.

`Reynolds number vector for Nusselt number` — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt
[100 150 100] (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из чисел Рейнольдса для табличной параметризации номера Nusselt. Этот вектор формирует независимую ось параметром Prandtl number vector for Nusselt number для 2D зависимого Nusselt number table. Векторные элементы должны быть перечислены в порядке возрастания и должны быть больше 0.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Prandtl number vector for Nusselt number` — Числа Прандтля, в которых можно свести в таблицу номер Nusselt
[1 10] (значение по умолчанию) | вектор из положительных безразмерных чисел

Вектор из чисел Прандтля для табличной параметризации номера Nusselt. Этот вектор формирует независимую ось параметром Reynolds number vector for Nusselt number для 2D зависимого Nusselt number table. Векторные элементы должны быть перечислены в порядке возрастания.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

`Nusselt number table` — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля
[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

M-by-N матрица цифр Nusselt в заданном Рейнольдсе и числах Прандтля. Линейная интерполяция используется между табличными элементами. M и N являются размерами соответствующих векторов:

M является количеством векторных элементов в параметре Reynolds number vector for Nusselt number.
N является количеством векторных элементов в параметре Prandtl number vector for Nusselt number.

Зависимости

Чтобы включить этот параметр, установите Heat transfer parameterization на Tabulated data - Nusselt number vs. Reynolds number & Prandtl number.

Начальные условия

`Initial liquid temperature` — Абсолютная температура в трубопроводе в начале симуляции
`293.15 K` (значение по умолчанию) | положительная скалярная величина или вектор в единицах температуры

Жидкая температура в начале симуляции в виде скаляра или вектора. Вектор n элементы долго задает жидкую температуру для каждого из сегментов трубопровода n. Если вектор является двумя элементами долго, температура вдоль трубопровода линейно распределяется между двумя значениями элемента. Если вектор является тремя или больше элементами долго, начальная температура в энном сегменте установлена энным элементом вектора.

`Initial liquid pressure` — Абсолютное давление в трубопроводе в начале симуляции
`0.101325 MPa` (значение по умолчанию) | положительная скалярная величина или вектор в единицах давления

Абсолютное жидкое давление в начале симуляции в виде скаляра или вектора. Вектор n элементы долго задает жидкое давление для каждого из сегментов трубопровода n. Если вектор является двумя элементами долго, давление вдоль трубопровода линейно распределяется между двумя значениями элемента. Если вектор является тремя или больше элементами долго, начальное давление в энном сегменте установлено энным элементом вектора.

Примеры модели

Содержите систему отопления

Смоделируйте простую систему отопления дома. Модель содержит нагреватель, контроллер и структуру дома с четырьмя излучателями и четырьмя комнатами. Каждая комната обменивается теплом со средой через ее наружные стены, крышу и окна. Каждый путь симулирован как комбинация тепловой конвекции, тепловой проводимости и количества тепла. Это принято, что тепло не передается внутренне между комнатами. Нагреватель состоит из печи, бойлера, аккумулятора и насоса, чтобы распространить горячую воду в системе. Диспетчер начинает допускать топливо в печь, если общая средняя температура комнат падает ниже 21 градуса по Цельсию, и это останавливается, если температура превышает 25 градусов по Цельсию. Симуляция вычисляет обогревающую стоимость и внутренние температуры.

Терморегулирование электромобиля

Моделирует систему терморегулирования электромобиля батареи. Система состоит из двух циклов хладагента, цикла охлаждения и каюты цикл HVAC. Тепловая нагрузка является батареями, трансмиссией и каютой.

Документация

Pipe (TL)

Описание

Передайте гибкость по каналу

Теплопередача в стенке трубопровода

Падение давления из-за вязкого трения

Баланс импульса

Передайте дискретизацию по каналу

Баланс массы

Энергетический баланс

Порты

Входной параметр

EL — Различие в вертикальном изменении порта физический сигнал

Сохранение

A — Открытие трубопровода тепловая жидкость

B — Открытие трубопровода тепловая жидкость

H — Передайте стенку по каналу тепловой

Параметры

Fluid dynamic compressibility — Смоделировать ли жидкую динамическую сжимаемость On (значение по умолчанию) | Off

Fluid inertia — Ли к ускорению жидкости модели On (значение по умолчанию) | Off

Зависимости

Number of segments — Передайте дискретизацию по каналу1 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Pipe total length — Общая длина трубопровода 5 m (значение по умолчанию) | положительная скалярная величина в единицах длины

Nominal cross-sectional area — Перекрестная частная область трубопровода без деформации0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

Pipe wall specification — Задает стенную гибкость Rigid (значение по умолчанию) | Flexible

Зависимости

Hydraulic diameter — Эффективный диаметр некруглых сечений 0.1128 m (значение по умолчанию) | положительная скалярная величина в единицах длины

Зависимости

Elevation gain specification — Установите свойство вертикального изменения трубопровода Constant (значение по умолчанию) | Variable

Зависимости

Static pressure-diameter compliance — Мера деформации трубопровода 1.2e-6 m/MPa (значение по умолчанию) | положительная скалярная величина в единицах длины/давления

Зависимости

Viscoelastic process time constant — Передайте постоянную времени деформации по каналу 0.01 s (значение по умолчанию) | положительная скалярная величина в модулях времени

Зависимости

Viscous friction parameterization — Модель Friction Haaland correlation (значение по умолчанию) | Nominal pressure drop vs. nominal mass flow rate | Tabulated data - Darcy friction factor vs. Reynolds number

Зависимости

Internal surface absolute roughness — Передайте стенку по каналу абсолютная шероховатость 1.5e-5 m (значение по умолчанию) | положительная скалярная величина в единицах длины

Зависимости

Shape factor for laminar flow viscous friction — Трение, постоянное для ламинарных течений64 (значение по умолчанию) | положительный безразмерный скаляр

Laminar flow upper Reynolds number limit — Число Рейнольдса, ниже которого поток ламинарен 2e+3 (значение по умолчанию) | положительный безразмерный скаляр

Turbulent flow lower Reynolds number limit — Число Рейнольдса, выше которого поток турбулентен 4e+3 (значение по умолчанию) | положительный безразмерный скаляр

Nominal mass flow rate — Передайте массовый расход жидкости по каналу [0.1 1] kg/s (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

Зависимости

Nominal pressure drop — Перепад давления по трубопроводу [0.001 0.01] MPa (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

Зависимости

Зависимости

Зависимости

Зависимости

Nusselt number for laminar flow heat transfer — Номер Nusselt, чтобы использовать в вычислениях теплопередачи для ламинарных течений3.66 (значение по умолчанию)

Зависимости

Nominal mass flow rate — Передайте массовый расход жидкости по каналу [0.1 1] kg/s (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

Зависимости

Nominal inflow temperature — Передайте входную температуру по каналу [293.15 293.15] K (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Зависимости

Nominal outflow temperature — Передайте выходную температуру по каналу [300 300] K'(значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Зависимости

Nominal inflow pressure — Передайте входное давление по каналу [0.101325 0.101325] MPa (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

Зависимости

Nominal wall temperature — Передайте температуру стенки по каналу [303.15 303.15] K (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

Зависимости

Coefficient a — Эмпирический постоянный a корреляции Диттуса-Болтера0.023 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent b — Эмпирический постоянный b корреляции Диттуса-Болтера0.8 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Exponent c — Эмпирический постоянный c корреляции Диттуса-Болтера0.4 (значение по умолчанию) | положительный безразмерный скаляр

Зависимости

Зависимости

Зависимости

Reynolds number vector for Nusselt number — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt[100 150 100] (значение по умолчанию) | вектор из положительных безразмерных чисел

Зависимости

Prandtl number vector for Nusselt number — Числа Прандтля, в которых можно свести в таблицу номер Nusselt[1 10] (значение по умолчанию) | вектор из положительных безразмерных чисел

Зависимости

Nusselt number table — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

Зависимости

Примеры модели

Содержите систему отопления

Терморегулирование электромобиля

Расширенные возможности

Генерация кода C/C++ Генерация кода C и C++ с помощью Simulink® Coder™.

`EL` — Различие в вертикальном изменении порта
физический сигнал

`A` — Открытие трубопровода
тепловая жидкость

`B` — Открытие трубопровода
тепловая жидкость

`H` — Передайте стенку по каналу
тепловой

`Fluid dynamic compressibility` — Смоделировать ли жидкую динамическую сжимаемость
`On` (значение по умолчанию) | `Off`

`Fluid inertia` — Ли к ускорению жидкости модели
`On` (значение по умолчанию) | `Off`

`Number of segments` — Передайте дискретизацию по каналу
1 (значение по умолчанию) | положительный безразмерный скаляр

`Pipe total length` — Общая длина трубопровода
`5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

`Nominal cross-sectional area` — Перекрестная частная область трубопровода без деформации
0.01 м^2 (значение по умолчанию) | положительная скалярная величина в единицах площади

`Pipe wall specification` — Задает стенную гибкость
`Rigid` (значение по умолчанию) | `Flexible`

`Hydraulic diameter` — Эффективный диаметр некруглых сечений
`0.1128 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

`Elevation gain specification` — Установите свойство вертикального изменения трубопровода
`Constant` (значение по умолчанию) | `Variable`

`Static pressure-diameter compliance` — Мера деформации трубопровода
`1.2e-6 m/MPa` (значение по умолчанию) | положительная скалярная величина в единицах длины/давления

`Viscoelastic process time constant` — Передайте постоянную времени деформации по каналу
`0.01 s` (значение по умолчанию) | положительная скалярная величина в модулях времени

`Viscous friction parameterization` — Модель Friction
`Haaland correlation` (значение по умолчанию) | `Nominal pressure drop vs. nominal mass flow rate` | `Tabulated data - Darcy friction factor vs. Reynolds number`

`Internal surface absolute roughness` — Передайте стенку по каналу абсолютная шероховатость
`1.5e-5 m` (значение по умолчанию) | положительная скалярная величина в единицах длины

`Shape factor for laminar flow viscous friction` — Трение, постоянное для ламинарных течений
64 (значение по умолчанию) | положительный безразмерный скаляр

`Laminar flow upper Reynolds number limit` — Число Рейнольдса, ниже которого поток ламинарен
`2e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Turbulent flow lower Reynolds number limit` — Число Рейнольдса, выше которого поток турбулентен
`4e+3` (значение по умолчанию) | положительный безразмерный скаляр

`Nominal mass flow rate` — Передайте массовый расход жидкости по каналу
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

`Nominal pressure drop` — Перепад давления по трубопроводу
`[0.001 0.01] MPa` (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

`Nusselt number for laminar flow heat transfer` — Номер Nusselt, чтобы использовать в вычислениях теплопередачи для ламинарных течений
3.66 (значение по умолчанию)

`Nominal mass flow rate` — Передайте массовый расход жидкости по каналу
`[0.1 1] kg/s` (значение по умолчанию) | скаляр или вектор из чисел в единицах массы/времени

`Nominal inflow temperature` — Передайте входную температуру по каналу
`[293.15 293.15] K` (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

`Nominal outflow temperature` — Передайте выходную температуру по каналу
`[300 300] K`'(значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

`Nominal inflow pressure` — Передайте входное давление по каналу
`[0.101325 0.101325] MPa` (значение по умолчанию) | скаляр или вектор из чисел в единицах давления

`Nominal wall temperature` — Передайте температуру стенки по каналу
`[303.15 303.15] K` (значение по умолчанию) | скаляр или вектор из чисел в единицах температуры

`Coefficient a` — Эмпирический постоянный a корреляции Диттуса-Болтера
0.023 (значение по умолчанию) | положительный безразмерный скаляр

`Exponent b` — Эмпирический постоянный b корреляции Диттуса-Болтера
0.8 (значение по умолчанию) | положительный безразмерный скаляр

`Exponent c` — Эмпирический постоянный c корреляции Диттуса-Болтера
0.4 (значение по умолчанию) | положительный безразмерный скаляр

`Reynolds number vector for Nusselt number` — Число Рейнольдса, в котором можно свести в таблицу номер Nusselt
[100 150 100] (значение по умолчанию) | вектор из положительных безразмерных чисел

`Prandtl number vector for Nusselt number` — Числа Прандтля, в которых можно свести в таблицу номер Nusselt
[1 10] (значение по умолчанию) | вектор из положительных безразмерных чисел

`Nusselt number table` — Цифры Nusselt в сведенном в таблицу Рейнольдсе и числах Прандтля
[ 3.72 4.21; 3.75 4.44; 4.21 7.15 ] (значение по умолчанию) | матрица положительных безразмерных чисел

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.