Synchronous Machine pu Standard
Динамика модели трехфазного круглого ротора или существенно-полюсной синхронной машины с помощью стандартных параметров в pu модулях
- Библиотека:
Simscape / Электрический / Специализированные Энергосистемы / Электрические Машины
Описание
Блок Synchronous Machine pu Standard моделирует синхронную машину в генераторе или моторном режиме с помощью стандартных параметров в pu модулях. Рабочий режим диктует знак механической энергии (положительный для режима генератора или отрицания для моторного режима). Электрическая часть машины представлена моделью в пространстве состояний шестого порядка, и механическая деталь эквивалентна в блоке Simplified Synchronous Machine.
Модель учитывает динамику статора, поля и обмоток демпфера. Эквивалентная схема модели представлена в системе координат ротора (система координат qd). Обмотки статора соединяются в Уае с внутренней нейтральной точкой. Все параметры ротора и электрические количества просмотрены от статора и идентифицированы запущенными переменными. Индексы:
d,q — d-и количество q-оси
R,s — Ротор и количество статора
l,m — Утечка и индуктивность намагничивания
f,k — Поле и демпфер извилистое количество
Электрическую модель машины показывают в этих схемах.
Динамическая модель с неравной взаимной индуктивностью
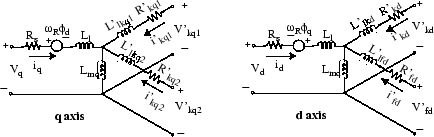
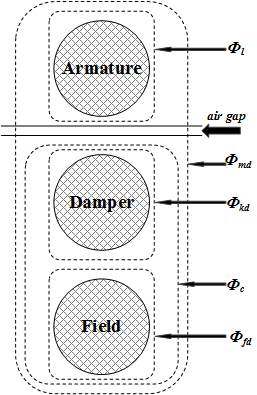
Обычная теория синхронного моделирования машины для анализа устойчивости принимает, что взаимная индуктивность между арматурой, демпфером и полем на обмотках прямой оси идентична. Обычно обмотки демпфера около воздушного зазора, и в результате поток, соединяющий схемы демпфера, почти равен арматуре соединения потока. Эта гипотеза производит приемлемые результаты для широкого спектра исследований устойчивости, особенно те на стороне сети. Однако когда дело доходит до поля текущие исследования, существует значительная ошибка. Динамическая модель эквивалентной схемы синхронной машины может включать дополнительную индуктивность, представляющую различие между полевым демпфером и полевой арматурой взаимная индуктивность на D-оси [1]. Эта индуктивность обычно называется Canay inductance. Индуктивность Canay соответствует потоку утечки, ΦC, в следующем рисунке и интерпретирована как корректирующий элемент в эквивалентной модели, которая может иметь отрицательную величину [2].
Стандарт IEEE 1110-2002 [3] подарки прямые и квадратичные оси синхронной динамической модели машины как показано в схемах.
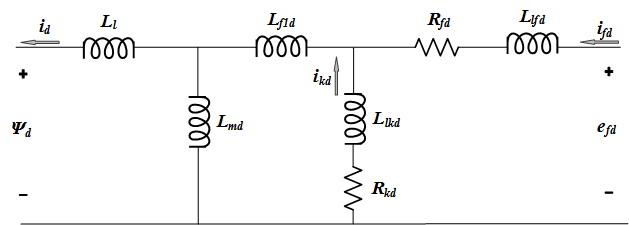
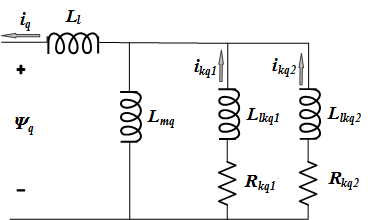
Соответствующие уравнения:
Допущения и ограничения
В дискретных системах, когда вы устанавливаете параметр Discrete solver model блока Synchronous Machine к Trapezoidal non iterative, вам придется соединить маленькую паразитную активную нагрузку на терминалах машины, чтобы избежать числовых колебаний. Времена большой выборки требуют больших загрузок. Минимальная активная нагрузка пропорциональна шагу расчета. Как показывает опыт, помните, что с 25 μs временными шагами в системе на 60 Гц, минимальная нагрузка составляет приблизительно 2,5% степени номинала машины. Например, 200 синхронных машин MVA в энергосистеме, дискретизированной с 50 μs шагами расчета, требуют приблизительно 5% активной нагрузки или 10 МВт. Если шаг расчета уменьшается до 20 μs, активная нагрузка 4 МВт должна быть достаточной.
Однако, если вы устанавливаете параметр Discrete solver model блока Synchronous Machine к Trapezoidal iterative (alg. loop), можно использовать незначительную паразитную загрузку (ниже 0,1% номинальной степени) при сохранении числовой устойчивости. Эта итеративная модель производит алгебраический цикл и приводит к более медленной скорости симуляции.
Порты
Входной параметр
Вывод
Сохранение
Параметры
Задайте стандартные параметры, также известные как операционные параметры, синхронной машины (такие столь же установившиеся, переходные, и/или подпереходные реактивные сопротивления и постоянные времени) как входные параметры с блоком. Как правило, производители машины обеспечивают операционные параметры.
В аналитическом программном обеспечении энергосистемы синхронные уравнения машины обычно решаются с помощью прямого нулевого квадратурой метода преобразования. Метод перевода данных вычисляет основные параметры от стандартных параметров [2], [3].
Настройка
Preset model — Электрические и механические параметры
No (значение по умолчанию) | 01: 50Hz 400V 8.1kVA 1500RPM | 02: 50Hz 400V 16kVA 1500RPM | ...
Набор предопределенных электрических и механических параметров для различных синхронных оценок машины степени (кВА), напряжение от фазы к фазе (V), частота (Гц) и оцененная скорость (об/мин).
Выберите одну из предварительно установленных моделей, чтобы загрузить соответствующие электрические и механические параметры. Выбор:
01: 50Hz 400V 8.1kVA 1500RPM02: 50Hz 400V 16kVA 1500RPM03: 50Hz 400V 31.3kVA 1500RPM04: 50Hz 400V 42.5kVA 1500RPM05: 50Hz 400V 60kVA 1500RPM06: 50Hz 400V 85kVA 1500RPM07: 50Hz 400V 250kVA 1500RPM08: 50Hz 400V 325kVA 1500RPM09: 50Hz 400V 670kVA 1500RPM10: 50Hz 400V 910kVA 1500RPM11: 50Hz 400V 1320kVA 1500RPM12: 50Hz 400V 2000kVA 1500RPM13: 60Hz 460V 10.2kVA 1800RPM14: 60Hz 460V 20kVA 1800RPM15: 60Hz 460V 37.5kVA 1800RPM16: 60Hz 460V 52.5kVA 1800RPM17: 60Hz 460V 72.5kVA 1800RPM18: 60Hz 460V 100kVA 1800RPM19: 60Hz 460V 300kVA 1800RPM20: 60Hz 460V 406kVA 1800RPM21: 60Hz 460V 800kVA 1800RPM22: 60Hz 460V 1075kVA 1800RPM23: 60Hz 460V 1588kVA 1800RPM24: 60Hz 460V 2500kVA 1800RPM
Выберите No (значение по умолчанию), если вы не хотите использовать предварительно установленную модель или если вы хотите изменить некоторые параметры предварительно установленной модели, аналогичной описанному ниже.
Когда вы выбираете предварительно установленную модель, электрические и механические параметры во вкладке Parameters недоступны. Начать с предварительно установленной модели и затем изменить параметры машины:
Выберите предварительно установленную модель, вы хотите инициализировать параметры.
Измените параметр Preset model в
No. Это действие не изменяет параметры машины, но повреждает связь с предварительно установленной моделью.Измените параметры машины, как вы хотите.
Mechanical input — Механический вход
Mechanical power Pm (значение по умолчанию) | Speed w | Mechanical rotational port
Представлять ли механическую энергию, применился к валу или скорости ротора как вход Simulink® блока, или представлять вал машины Simscape™ вращательный механический порт.
Выберите Mechanical power Pm задавать вход механической энергии, в pu, и осушать порт Pm. Скорость машины определяется инерцией постоянный H и различием между механическим крутящим моментом Tm, который следует из поданного механического питания Pm и внутренний электромагнитный крутящий момент Te. Когда скорость положительна, положительный сигнал механической энергии указывает на режим генератора, и отрицательный сигнал указывает на моторный режим.
Выберите Speed w задавать вход скорости в pu и осушать порт w. Скорость машины наложена, и механическая деталь модели (инерция постоянный H) проигнорирована. Используя скорость, когда механический вход позволяет вам моделировать механическое устройство, связывающееся между двумя машинами.
Следующая фигура указывает, как смоделировать жесткое соединение вала в моторной генераторной установке, где обе машины являются синхронными машинами.
Скорость выход машины 1 (двигатель) соединяется с входом скорости машины 2 (генератор). В этом рисунке момент трения проигнорирован в машине 2. Поэтому его электромагнитный крутящий момент, выход Te соответствует механическому крутящему моменту Tm, применился к валу машины 1. Соответствующая механическая входная мощность машины 1 вычисляется как Pm = Tm *w. Фактор Kw учитывает единицы скорости обеих машин (pu) и отношения коробки передач w2/w1. Фактор KT учитывает модули крутящего момента обеих машин (pu) и оценок машины. Кроме того, потому что инерция, J2 проигнорирован в машине 2, J2, относится к скорости машины 1 и должна быть добавлена, чтобы обработать машинным способом 1 инерцию, J1.
Выберите Mechanical rotational port осушать порт вращательного механического устройства Simscape, S, который позволяет вам подключению вала машины к другому валу машины или с другими блоками Simscape, которые имеют порты вращательного механического устройства.
Фигура указывает, как соединить блок Ideal Torque Source от библиотеки Simscape до порта вала машины, чтобы представлять машину в моторном режиме или режиме генератора, когда скорость ротора положительна.
Rotor type — Тип ротора
Salient-pole (значение по умолчанию) | Round
Задайте тип ротора как любой Salient-pole или Round (цилиндрический). Установка влияет на количество схем ротора на q-оси (обмотки демпфера).
Use signal names to identify bus labels — Как идентифицировать метки шины
off (значение по умолчанию) | on
Когда этот флажок устанавливается, измерение, выход использует имена сигнала, чтобы идентифицировать метки шины. Выберите эту опцию для приложений, которые требуют, чтобы метки сигнала шины имели только алфавитно-цифровые символы.
Когда этот флажок снимается, измерение, выход использует определение сигнала, чтобы идентифицировать метки шины. Метки содержат неалфавитно-цифровые символы, которые несовместимы с некоторыми приложениями Simulink.
Параметры
Nominal power, line-to-line voltage, frequency [ Pn(VA) Vn(Vrms) fn(Hz) ] — Номинальная степень, линия к линейному напряжению и частота
[6e+04 400 50] (значение по умолчанию) | трехэлементный вектор
Общая трехфазная полная мощность (ВА), линия к линейному напряжению RMS (pu), частота (Гц) и поле, текущее (pu).
Этот параметр идентичен параметру Nominal power, voltage, frequency, field current [ Pn(VA) Vn(Vrms) fn(Hz) ifn(A) ] блока Synchronous Machine SI Fundamental, за исключением того, что вы не задаете номинальное текущее поле. Это значение не требуется, потому что блоку Synchronous Machine pu Standard не нужен коэффициент трансформации. Поскольку количества ротора просматриваются от статора, они преобразованы в pu использование базовых количеств статора, выведенных из предшествования трем номинальным параметрам.
Reactances [ Xd Xd' Xd'' Xq Xq'' Xl ] (pu) — Реактивные сопротивления
[2.24 0.17 0.12 1.02 0.13 0.08]
d - ось синхронное реактивное сопротивление Xd, переходное реактивное сопротивление Xd' и подпереходное реактивное сопротивление Xd''; q - ось синхронное реактивное сопротивление Xq и подпереходное реактивное сопротивление Xq''; и реактивное сопротивление утечки Xl (все в pu).
Зависимости
Чтобы включить этот параметр, установите Rotor type на Salient-pole.
Reactances [ Xd Xd' Xd'' Xq Xq' Xq'' Xl ] (pu) — Реактивные сопротивления
[ 1.81, 0.3, 0.23, 1.76, 0.65, 0.25, 0.15 ]
d - ось синхронное реактивное сопротивление Xd, переходное реактивное сопротивление Xd' и подпереходное реактивное сопротивление Xd''; q - ось синхронное реактивное сопротивление Xq, переходное реактивное сопротивление Xq' и подпереходное реактивное сопротивление Xq''; и реактивное сопротивление утечки Xl (все в pu).
Зависимости
Чтобы включить этот параметр, установите Rotor type на Round.
d axis — d - постоянная времени оси
Short-circuit (значение по умолчанию) | Open-circuit
Постоянная времени для оси d.
q axis — q - постоянная времени оси
Short-circuit (значение по умолчанию) | Open-circuit
Постоянная времени для оси q.
[ Tdo' Tdo'' Tqo'' ] (s) — Постоянные времени в s
[ 4.4849 0.0681 0.1 ]
Постоянные времени, все в s, для следующего:
d- переходная разомкнутая цепь оси (Tdo')
d- подпереходная разомкнутая цепь оси (Tdo'')
q- подпереходная разомкнутая цепь оси (Tqo'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Salient-pole, d axis к Open-circuit, и q axis к Open-circuit.
[ Tdo' Tdo'' Tqo' Tqo'' ] (s) — Постоянные времени в s
[ 8.0, 0.03, 1.0, 0.07 ]
Постоянные времени, все в s, для следующего:
d- переходная разомкнутая цепь оси (Tdo')
d- подпереходная разомкнутая цепь оси (Tdo'')
q- переходная разомкнутая цепь оси (Tqo')
q- подпереходная разомкнутая цепь оси (Tqo'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Round, d axis к Open-circuit, и q axis к Open-circuit.
[ Tdo' Tdo'' Tq'' ] (s) — Постоянные времени в s
[ 4.49 0.0681 0.0513 ]
Постоянные времени, все в s, для следующего:
d- переходная разомкнутая цепь оси (Tdo')
d- подпереходная разомкнутая цепь оси (Tdo'')
q- подпереходная короткая схема оси (Tq'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Salient-pole, d axis к Open-circuit, и q axis к Short-circuit.
[ Tdo' Tdo'' Tq' Tq'' ] (s) — Постоянные времени в s
[ 8.0, 0.03, 0.3371, 0.0295 ]
Постоянные времени, все в s, для следующего:
d- переходная разомкнутая цепь оси (Tdo')
d- подпереходная разомкнутая цепь оси (Tdo'')
q- переходная короткая схема оси (Tq')
q- подпереходная короткая схема оси (Tq'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Round, d axis к Open-circuit, и q axis к Short-circuit.
[ Td' Td'' Tqo'' ] (s) — Постоянные времени в s
[ 1.01, 0.053, 0.1 ]
Постоянные времени, все в s, для следующего:
d- переходная короткая схема оси (Td')
d- подпереходная короткая схема оси (Td'')
q- подпереходная разомкнутая цепь оси (Tqo'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Salient-pole, d axis к Short-circuit, и q axis к Open-circuit.
[ Td' Td'' Tqo' Tqo'' ] (s) — Постоянные времени в s
[ 1.3201, 0.023, 1.0, 0.07 ]
Постоянные времени, все в s, для следующего:
d- переходная короткая схема оси (Td')
d- подпереходная короткая схема оси (Td'')
q- переходная разомкнутая цепь оси (Tqo')
q- подпереходная разомкнутая цепь оси (Tqo'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Round, d axis к Short-circuit, и q axis к Open-circuit.
[ Td' Td'' Tq'' ] (s) — Постоянные времени в s
[0.012 0.003 0.003]
Постоянные времени, все в s, для следующего:
d- переходная короткая схема оси (Td')
d- подпереходная короткая схема оси (Td'')
q- подпереходная короткая схема оси (Tq'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Salient-pole, d axis к Short-circuit, и q axis к Short-circuit.
[ Td' Td'' Tq' Tq'' ] (s) — Постоянные времени в s
[ 1.3201, 0.0231, 0.3371, 0.0295 ]
Постоянные времени, все в s, для следующего:
d- переходная короткая схема оси (Td')
d- подпереходная короткая схема оси (Td'')
q- переходная короткая схема оси (Tq')
q- подпереходная короткая схема оси (Tq'')
Зависимости
Чтобы включить этот параметр, установите Rotor type на Round, d axis к Short-circuit, и q axis к Short-circuit.
Stator resistance Rs (pu) — Сопротивление статора
0.037875
Сопротивление статора Rs, в pu.
Inertia coefficient, friction factor, pole pairs [ H(s) F(pu) p()] — Коэффициент инерции, коэффициент трения и пары полюса
[0.1028 0.02056 2]
Постоянный H инерции, который является отношением энергии, сохраненной в роторе на номинальной скорости по номинальной степени машины, коэффициент трения F (pu torque/pu скорость), и количество пар полюса p. Tf момента трения пропорционален скорости ротора ω (Tf = F.ω, где все количества описываются в pu).
Зависимости
Чтобы включить этот параметр, установите Mechanical input на Mechanical power Pm или Mechanical rotational port.
Pole pairs p () — Пары полюса
20
Количество пар полюса синхронной машины.
Зависимости
Чтобы включить этот параметр, установите Mechanical input на Speed w.
Initial conditions [ dw(%) th(deg) ia,ib,ic(pu) pha,phb,phc(deg) Vf(pu) ] — Начальные условия
[ 0 0 0 0 0 0 0 0 1 ]
Начальное отклонение скорости Δω (процент номинальной скорости), электрический угол ротора Θe (степени), линия текущие величины ia, ib, ic (pu) и углы фазы pha, phb, phc (степени) и начальное полевое напряжение Vf (pu). Можно вычислить эти значения автоматически при помощи инструмента Load Flow или инструмента Machine Initialization блока powergui.
Simulate saturation — Симулируйте магнитное насыщение
on (значение по умолчанию) | off
Симулировано ли магнитное насыщение ротора и железа статора.
Установите этот флажок, чтобы обеспечить матрицу параметров для симуляции насыщения.
Снимите этот флажок к не насыщение модели в вашей симуляции. В этом случае отношение между ifd и Vt линейно (никакое насыщение).
[ ifd; vt] (pu) — Параметры кривой насыщения без загрузок
[0.6404,0.7127,0.8441,0.9214,0.9956,1.082,1.19,1.316,1.457;0.7,0.7698,0.8872,0.9466,0.9969,1.046,1.1,1.151,1.201]
Параметры кривой насыщения без загрузок. Магнитное насыщение статора и железа ротора моделируется кусочными точками определения линейного соотношения на кривой насыщения без загрузок. Первая строка этой матрицы содержит значения полевых токов (в pu). Вторая строка содержит значения соответствующих терминальных напряжений (в pu). Первая точка (первый столбец матрицы) должна отличаться от [0,0]. Эта точка соответствует точке, где эффект насыщения начинается. Для насыщения, номинальное поле текущая и номинальная линия к линейному напряжению RMS базовые значения для поля текущее и терминальное напряжение, соответственно.
Нажмите Plot, чтобы просмотреть кривую насыщения без загрузок.
Зависимости
Чтобы включить этот параметр, выберите Simulate saturation.
Усовершенствованный
Чтобы включить вкладку Advanced, в блоке powergui, устанавливают Simulation type на Discrete и очистите Automatically handle discrete solver.
Sample time (-1 for inherited) — Шаг расчета для блока
-1
Шаг расчета используется блоком. Чтобы наследовать шаг расчета, заданный в блоке powergui, установите этот параметр на −1.
Discrete solver model — Метод интегрирования
Trapezoidal non iterative (значение по умолчанию) | Trapezoidal iterative (alg. loop) | Trapezoidal robust | Backward Euler robust
Метод интегрирования, используемый блоком, когда параметр Solver type блока powergui устанавливается на Discrete.
Discrete solver model автоматически установлен в Trapezoidal robust когда вы выбираете параметр Automatically handle Discrete solver and Advanced tab solver settings of blocks блока powergui.
Trapezoidal non iterative и Trapezoidal iterative (alg. loop) методы больше не рекомендуются для дискретизации блока Synchronous Machine pu Standard. Trapezoidal non iterative требует, чтобы вы добавили ненезначительные загрузки шунта на терминалах машины, чтобы гарантировать устойчивость симуляции и Trapezoidal iterative (alg. loop) может не сходиться и заставляет симуляцию останавливаться, когда количество машин увеличивается в модели.
Trapezoidal robust и Backward Euler robust методы позволяют вам избавлять от необходимости использовать паразитные загрузки и симулировать машину без загрузок. Устранить топологические ошибки машин, соединенных с индуктивной схемой (например, выключатель, соединенный последовательно с машиной); машина моделирует незначительную внутреннюю загрузку 0,01% номинальной степени.
Trapezoidal robust метод немного более точен, чем Backward Euler robust метод, особенно когда модель симулирована в больших шагах расчета. Trapezoidal robust метод может произвести небольшие ослабленные числовые колебания на напряжении машины при условиях без загрузок, в то время как Backward Euler robust метод предотвращает колебания и обеспечивает хорошую точность.
Для получения дополнительной информации о какой метод использовать в вашем приложении, смотрите Симуляцию Дискретизированные Электрические системы.
Загрузите поток
Параметры потока загрузки используются, чтобы задать параметры блоков для использования с инструментом Load Flow блока powergui. Эти параметры потока загрузки используются для инициализации модели только. Они не оказывают влияния на модель блока или на эффективность симуляции.
Generator type — Тип генератора машины
PV (значение по умолчанию) | swing | PQ
Тип генератора машины. Выбор:
swing— Реализует величину управления генератора и угол фазы ее терминального напряжения. Ссылочная величина напряжения и угол заданы Swing bus or PV bus voltage и параметрами Swing bus voltage angle блока Load Flow Bus, соединенного с терминалами машины.PV— Реализует генератор, управляющий его выходом активная степень P и величина напряжения V. P задан параметром Active power generation P (W) блока. V задан параметром Swing bus or PV bus voltage блока Load Flow Bus, соединенного с терминалами машины. Можно управлять минимальной и максимальной реактивной энергией, произведенной блоком при помощи параметров Maximum reactive power Qmax (var) и Minimum reactive power Qmin (var).PQ— Реализует генератор, управляющий его выходом активная степень P и реактивная мощность Q. P и Q заданы Active power generation P (W) и параметрами Reactive power generation Q (var) блока, соответственно.
Active power generation P (W) — Активная энергия произведена машиной
0
Активная степень, которую вы хотите сгенерированный машиной в ваттах. Когда машина действует в моторном режиме, вы задаете отрицательную величину.
Зависимости
Чтобы включить этот параметр, установите Generator type на PV или PQ.
Reactive power generation Q (var) — Реактивная энергия произведена машиной
0
Реактивная мощность, которую вы хотите сгенерированный машиной в Варе. Отрицательная величина указывает, что реактивная мощность поглощена машиной.
Зависимости
Чтобы включить этот параметр, установите Generator type на PQ.
Minimum reactive power Qmin (var) — Минимальная реактивная энергия произведена машиной
-inf (значение по умолчанию) | скаляр
Минимальная реактивная энергия, которая может быть произведена машиной при хранении терминального напряжения в его ссылочном значении. Это ссылочное напряжение задано параметром Swing bus or PV bus voltage блока Load Flow Bus, соединенного с терминалами машины. Значением по умолчанию является -inf, что означает, что нет никакого нижнего предела на реактивной мощности выхода.
Зависимости
Чтобы включить этот параметр, установите Generator type на PV.
Maximum reactive power Qmax (var) — Максимальная реактивная энергия произведена машиной
inf (значение по умолчанию) | скаляр
Максимальная реактивная энергия, которая может быть произведена машиной при хранении терминального напряжения в его ссылочном значении. Это ссылочное напряжение задано параметром Swing bus or PV bus voltage блока Load Flow Bus, соединенного с терминалами машины. Значением по умолчанию является inf, что означает, что нет никакого верхнего предела реактивной мощности выхода.
Зависимости
Чтобы включить этот параметр, установите Generator type на PV.
Примеры
power_thermal пример использует блок Synchronous Machine pu Standard, чтобы смоделировать подсинхронный резонанс (SSR) в паровой турбине и регуляторе в компенсированной ряду сети.
Ссылки
[1] Canay, I.M. "Причины Несоответствий на Вычислении Количеств Ротора и Точных Эквивалентных Схемах Синхронной Машины". IEEE®Transactions на Аппарате Степени и Системах. PAS-88, № 7 (1969): 1114–1120.
[2] Moeini, A., и др. “Синхронная модель Machine Stability, Обновление Станд. IEEE 1110-2002 Метода Перевода Данных”. Заседания стандартов IEEE. 2018.
[3] Руководство IEEE для синхронных методов моделирования генератора и приложения в исследованиях устойчивости энергосистемы. Станд. IEEE 1110-2002 (Версия станд. IEEE 1110-1991 [2003]): 1–72.
[4] Краузе, P.C. Анализ электрического машинного оборудования. Разделите 12.5. Нью-Йорк: McGraw-Hill, 1986.
[5] Kundur, P. Устойчивость энергосистемы и управление. Нью-Йорк, McGraw-Hill, 1994.
Расширенные возможности
Смотрите также
Excitation System | Hydraulic Turbine and Governor | powergui | Simplified Synchronous Machine | Steam Turbine and Governor | Synchronous Machine pu Fundamental | Synchronous Machine SI Fundamental