Управление поиском экстремума (ESC) является алгоритмом адаптивного управления в реальном времени, без моделей, который полезен для адаптации к неизвестной системной динамике и неизвестным отображениям от параметров управления до целевой функции. Можно использовать экстремум, стремящийся решить статические задачи оптимизации и оптимизировать параметры динамических систем.
Экстремум, ища алгоритм использует следующие этапы, чтобы настроить значение параметров.
Модуляция — Тревожит значение параметра, оптимизируемого с помощью низкой амплитуды синусоидальный сигнал.
Отклик системы — оптимизируемая система реагирует на возмущения параметра. Эта реакция вызывает соответствующее изменение в значении целевой функции.
Демодуляция — Умножает сигнал целевой функции на синусоиду с той же частотой как сигнал модуляции. Этот этап включает дополнительный фильтр высоких частот, чтобы удалить смещение из сигнала целевой функции.
Обновление параметра — Обновление значение параметров путем интеграции демодулируемого сигнала. Значение параметров соответствует состоянию интегратора. Этот этап включает дополнительный фильтр lowpass, чтобы удалить высокочастотный шум из демодулируемого сигнала.
Программное обеспечение Simulink® Control Design™ реализует этот алгоритм с помощью блока Extremum Seeking Control. Для примеров ищущего экстремум управления см.:
Чтобы продемонстрировать поиск экстремума, рассмотрите следующую статическую задачу оптимизации.
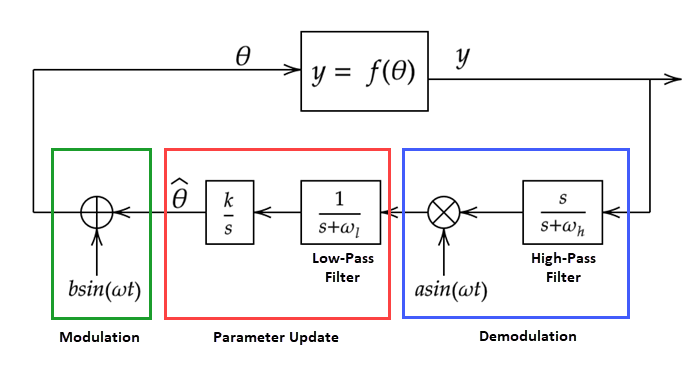
Здесь:
предполагаемое значение параметров.
θ является сигналом модуляции
y = f (θ) является функциональный максимизируемый выход, то есть, целевая функция.
ω является частотой принуждения сигналов модуляции и демодуляции.
b· (ωt) является сигналом модуляции.
a· (ωt) является сигналом демодуляции.
ωl является частотой среза фильтра lowpass.
ωh является частотой среза фильтра высоких частот.
k является скоростью обучения.
Оптимальное значение параметров, θ*, происходит в максимальном значении f (θ).
Чтобы оптимизировать несколько параметров, вы используете отдельный настраивающий цикл для каждого параметра.
Следующая фигура демонстрирует экстремум, ищущий увеличивающийся фрагмент кривой целевой функции. Модулируемый θ сигнала является суммой текущего предполагаемого параметра и сигнала модуляции. Применение f (θ) производит встревоженную целевую функцию с той же фазой как сигнал модуляции. Умножение встревоженной целевой функции сигналом демодуляции производит положительный сигнал. Интеграция этого сигнала увеличивает значение θ, который двигает его поближе к пику целевой функции.
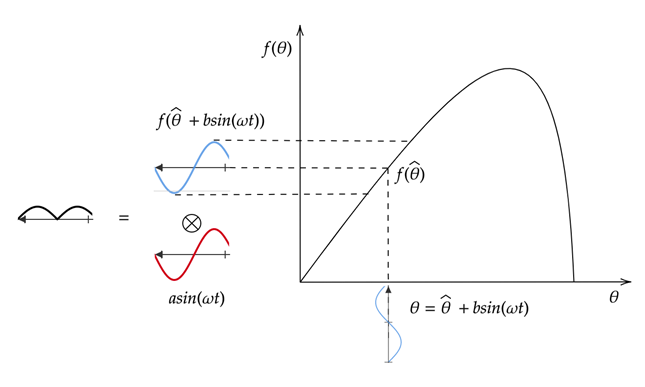
Следующая фигура демонстрирует экстремум, ищущий уменьшающийся фрагмент кривой целевой функции. В этом случае применение f (θ) производит встревоженную целевую функцию, которая является 180 градусами pf фаза от сигнала модуляции. Умножение на сигнал демодуляции производит отрицательный сигнал. Интеграция этого сигнала уменьшает значение θ, который двигает его поближе к пику целевой функции.
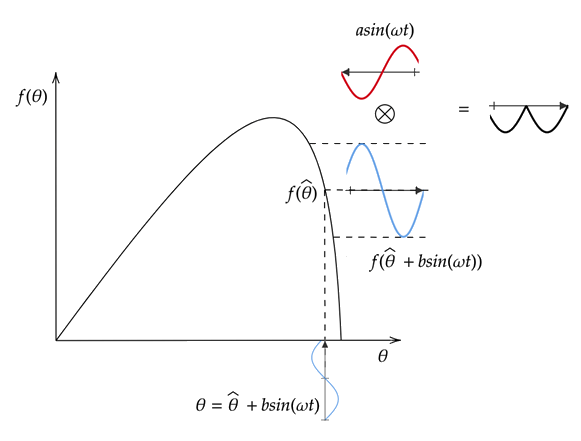
Следующее изображение демонстрирует экстремум, ищущий плоский фрагмент кривой целевой функции, то есть, фрагмент кривой около максимума. В этом случае применение f (θ) производит встревоженную целевую функцию почти нуля. Интеграция этого сигнала не значительно изменяет значение θ, который уже является около его оптимального значения θ*.
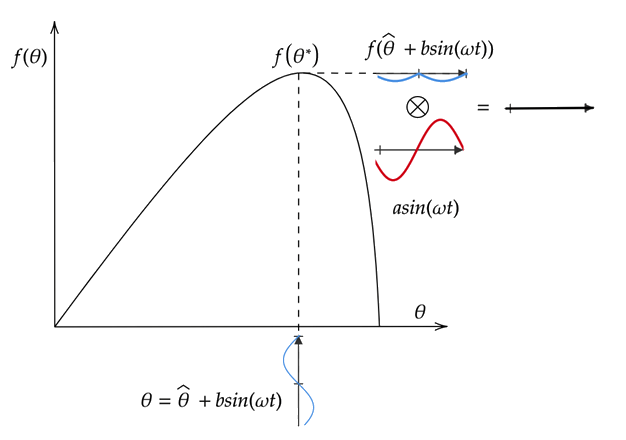
Оптимизация поиска экстремума динамической системы происходит подобным способом как статическая оптимизация. Однако в этом случае параметр θ влияет на выход зависящей от времени динамической системы. Целевая функция, которая будет максимизироваться, вычисляется из системы выход. Следующий рисунок показывает общий настраивающий цикл для динамической системы.
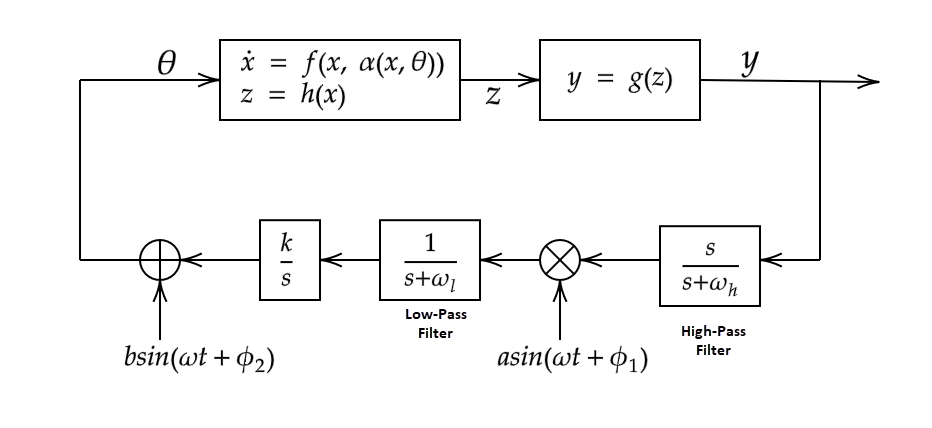
Здесь:
функция состояния динамической системы.
z = h (x) является выход динамической системы.
y = g (z) является целевой функцией, выведенной из выхода динамической системы.
ϕ 1 является фазой сигнала демодуляции.
ϕ 2 является фазой сигнала модуляции.
При разработке ищущего экстремум контроллера рассмотрите следующие инструкции.
Убедитесь, что системные движущие силы находятся на самом быстром масштабе времени, частоты принуждения находятся на среднем масштабе времени, и частоты среза фильтра находятся на самом медленном масштабе времени.
Задайте амплитуду для сигнала демодуляции, который очень больше, модуляция сигнализируют об амплитуде (a ≫ b).
Выберите углы фазы для модуляции, и демодуляция сигнализирует таким образом что because(ϕ 1 – ϕ 2)> 0.
При настройке нескольких параметров частота принуждения для каждого настраивающего цикла должна отличаться.
Попытайтесь проектировать свою систему без фильтров lowpass и высокой передачи. Если эффективность не является удовлетворительной, можно затем рассмотреть добавление того или обоих фильтров.
[1] Ariyur, Картик Б. и Мирослав Крстик. Оперативная оптимизация управлением поиском экстремума. Хобокен, NJ: межнаука Вайли, 2003.