Модели линейной регрессии описывают линейное соотношение между ответом и одним или несколькими прогнозирующими условиями. Много раз, однако, нелинейное отношение существует. Нелинейная Регрессия описывает общие нелинейные модели. Специальный класс нелинейных моделей, названных обобщенными линейными моделями, использует методы Linear.
Вспомните, что линейные модели имеют эти характеристики:
В каждом множестве значений для предикторов ответ имеет нормальное распределение со средним μ.
Вектор коэффициентов b задает линейную комбинацию X b предикторов X.
Моделью является μ = X b.
В обобщенных линейных моделях эти характеристики обобщены можно следующим образом:
В каждом множестве значений для предикторов ответ имеет распределение, которое может быть нормальным, биномиальным, Пуассон, гамма или Гауссова инверсия, параметрами включая средний μ.
Вектор коэффициентов b задает линейную комбинацию X b предикторов X.
Чтобы начать соответствовать регрессии, поместите свои данные в форму, которую ожидают подходящие функции. Все методы регрессии начинаются с входных данных в массиве X и данные об ответе в отдельном векторе y, или входные данные в таблице или массиве набора данных tbl и данные об ответе как столбец в tbl. Каждая строка входных данных представляет одно наблюдение. Каждый столбец представляет один предиктор (переменная).
Для таблицы или массива набора данных tbl, укажите на переменную отклика с 'ResponseVar' пара "имя-значение":
mdl = fitglm(tbl,'ResponseVar','BloodPressure');
Переменная отклика является последним столбцом по умолчанию.
Можно использовать числовые предикторы categorical. Категориальный предиктор является тем, который принимает значения от фиксированного набора возможностей.
Для числового массива X, укажите на категориальные предикторы с помощью 'Categorical' пара "имя-значение". Например, чтобы указать на это предикторы 2 и 3 из шесть являются категориальными:
mdl = fitglm(X,y,'Categorical',[2,3]); % or equivalently mdl = fitglm(X,y,'Categorical',logical([0 1 1 0 0 0]));
Для таблицы или массива набора данных tbl, подходящие функции принимают, что эти типы данных являются категориальными:
Логический вектор
Категориальный вектор
Массив символов
Массив строк
Если вы хотите указать, что числовой предиктор является категориальным, используйте 'Categorical' пара "имя-значение".
Представляйте недостающие числовые данные как NaN. Чтобы представлять недостающие данные для других типов данных, смотрите Значения Missing Group.
Для 'binomial' модель с матрицей данных X, ответ y может быть:
Вектор столбца двоичных данных — Каждая запись представляет успех (1) или отказ (0).
Матрица 2D столбца целых чисел — первый столбец является количеством успехов в каждом наблюдении, второй столбец является количеством испытаний в том наблюдении.
Для 'binomial' модель с таблицей или набором данных tbl:
Используйте ResponseVar пара "имя-значение", чтобы задать столбец tbl это дает количество успехов в каждом наблюдении.
Используйте BinomialSize пара "имя-значение", чтобы задать столбец tbl это дает количество испытаний в каждом наблюдении.
Например, чтобы создать массив набора данных из электронной таблицы Excel®:
ds = dataset('XLSFile','hospital.xls',... 'ReadObsNames',true);
Создать массив набора данных из переменных рабочей области:
load carsmall
ds = dataset(MPG,Weight);
ds.Year = ordinal(Model_Year);Составлять таблицу от переменных рабочей области:
load carsmall
tbl = table(MPG,Weight);
tbl.Year = ordinal(Model_Year);Например, чтобы создать числовые массивы из переменных рабочей области:
load carsmall
X = [Weight Horsepower Cylinders Model_Year];
y = MPG;Создать числовые массивы из электронной таблицы Excel:
[X, Xnames] = xlsread('hospital.xls'); y = X(:,4); % response y is systolic pressure X(:,4) = []; % remove y from the X matrix
Заметьте, что нечисловые записи, такие как sex, не появляйтесь в X.
Часто, ваши данные предлагают тип распределения обобщенной линейной модели.
| Тип данных ответа | Предложенный тип распределения модели |
|---|---|
| Любое вещественное число | 'normal' |
| Любое положительное число | 'gamma' или 'inverse gaussian' |
| Любое неотрицательное целое число | 'poisson' |
Целое число от 0 до n, где n фиксированное положительное значение | 'binomial' |
Установите тип распределения модели с Distribution пара "имя-значение". После выбора вашего типа модели выберите функцию ссылки, чтобы сопоставить между средним µ и линейным предиктором Xb.
| Значение | Описание |
|---|---|
'comploglog' | журнал (-журнал ((1 – µ))) = Xb |
| µ = Xb |
| регистрируйте (µ) = Xb |
| журнал (µ / (1 – µ)) = Xb |
| журнал (-журнал (µ)) = Xb |
'probit' | Φ–1 (µ) = Xb, где Φ является нормальной (Гауссовой) кумулятивной функцией распределения |
'reciprocal', значение по умолчанию для распределения 'gamma' | µ –1 = Xb |
| µ p = Xb |
Массив ячеек формы | Заданная пользователями функция ссылки (см. Функцию Настраиваемой ссылки), |
Функции ссылки не по умолчанию в основном полезны для биномиальных моделей. Этими функциями ссылки не по умолчанию является 'comploglog'loglog, и 'probit'.
Функция ссылки задает отношение f (µ) = Xb между средним ответом µ и линейной комбинацией Xb = X *b предикторов. Можно выбрать одну из встроенных функций ссылки или задать собственное путем определения функции ссылки FL, его производный FD, и его обратный FI:
Функция ссылки FL вычисляет f (µ).
Производная ссылки функционирует FD вычисляет df (µ)/dµ.
Обратная функция FI вычисляет g (Xb) = µ.
Можно задать функцию настраиваемой ссылки любым из двух эквивалентных способов. Каждый путь содержит указатели на функцию, которые принимают единый массив значений, представляющих µ или Xb, и возвращает массив тот же размер. Указатели на функцию или в массиве ячеек или в структуре:
Массив ячеек формы {FL FD FI}, содержа три указателя на функцию, созданное использование @, это задает ссылку (FL), производная ссылки (FD), и обратная ссылка (FI).
Структуры@:
s.Link
s.Derivative
s.Inverse
Например, чтобы подбирать модель с помощью 'probit' функция ссылки:
x = [2100 2300 2500 2700 2900 ... 3100 3300 3500 3700 3900 4100 4300]'; n = [48 42 31 34 31 21 23 23 21 16 17 21]'; y = [1 2 0 3 8 8 14 17 19 15 17 21]'; g = fitglm(x,[y n],... 'linear','distr','binomial','link','probit')
g =
Generalized Linear regression model:
probit(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Можно выполнить ту же подгонку с помощью функции настраиваемой ссылки, которая выполняет тождественно к 'probit' функция ссылки:
s = {@norminv,@(x)1./normpdf(norminv(x)),@normcdf};
g = fitglm(x,[y n],...
'linear','distr','binomial','link',s)g =
Generalized Linear regression model:
link(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Эти две модели являются тем же самым.
Эквивалентно, можно записать s как структура вместо cell-массива указателей на функцию:
s.Link = @norminv; s.Derivative = @(x) 1./normpdf(norminv(x)); s.Inverse = @normcdf; g = fitglm(x,[y n],... 'linear','distr','binomial','link',s)
g =
Generalized Linear regression model:
link(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Существует два способа создать подобранную модель.
Использование fitglm когда у вас есть хорошая идея вашей обобщенной линейной модели, или, когда это необходимо, настроить вашу модель позже, чтобы включать или исключить определенные условия.
Использование stepwiseglm когда это необходимо, подбирать вашу модель с помощью ступенчатой регрессии. stepwiseglm начинает с одной модели, такой как константа, и добавляет или вычитает условия по одному, выбирая оптимальный термин каждый раз в жадном виде, пока она не может улучшиться далее. Использование, пошагово соответствующее, чтобы найти хорошую модель, та, которая имеет только соответствующие условия.
Результат зависит от стартовой модели. Обычно, начиная с постоянной модели приводит к маленькой модели. Начиная с большего количества условий может привести к более сложной модели, но тот, который имеет более низкую среднеквадратическую ошибку.
В любом случае предоставьте модель подходящей функции (который является стартовой моделью для stepwiseglm).
Задайте модель с помощью одного из этих методов.
| Имя | Тип модели |
|---|---|
'constant' | Модель содержит только константу (точка пересечения) термин. |
'linear' | Модель содержит точку пересечения и линейные члены для каждого предиктора. |
'interactions' | Модель содержит точку пересечения, линейные члены и все продукты пар отличных предикторов (никакие условия в квадрате). |
'purequadratic' | Модель содержит точку пересечения, линейные члены, и придает условиям квадратную форму. |
'quadratic' | Модель содержит точку пересечения, линейные члены, взаимодействия, и придает условиям квадратную форму. |
'poly | Модель является полиномом со всеми условиями до степени i в первом предикторе, степень j во втором предикторе, и т.д. Используйте цифры 0 через 9. Например, 'poly2111' имеет константу плюс все линейные члены и множители, и также содержит условия с предиктором 1 в квадрате. |
Матрица условий T t (p + 1) матричные условия определения в модели, где t является количеством условий, p является количеством переменных предикторов и +1 счетом на переменную отклика. Значение T(i,j) экспонента переменной j в термине i.
Например, предположите, что вход включает три переменных предиктора x1x2 , и x3 и переменная отклика y в порядке x1x2 , x3, и y. Каждая строка T представляет один термин:
[0 0 0 0] — Постоянный термин или точка пересечения
[0 1 0 0] x2 ; эквивалентно, x1^0 * x2^1 * x3^0
[1 0 1 0] — x1*x3
[2 0 0 0] — x1^2
[0 1 2 0] — x2*(x3^2)
0 в конце каждого термина представляет переменную отклика. В общем случае вектор-столбец из нулей в матрице условий представляет положение переменной отклика. Если у вас есть переменные прогноза и переменные отклика в матрице и вектор-столбце, то необходимо включать 0 для переменной отклика в последнем столбце каждой строки.
Формула для спецификации модели является вектором символов или строковым скаляром формы
Y ~ terms'
y имя ответа.
terms содержит
Имена переменных
+ включать следующую переменную
- исключить следующую переменную
: задавать взаимодействие, продукт условий
* задавать взаимодействие и все условия более низкоуровневые
^ возводить предиктор в степень, точно так же, как в * повторный, таким образом, ^ включает условия более низкоуровневые также
() к условиям группы
Совет
Формулы включают константу (точка пересечения) термин по умолчанию. Чтобы исключить постоянный термин из модели, включайте -1 в формуле.
Примеры:
'y ~ x1 + x2 + x3' линейная модель с тремя переменными с точкой пересечения.
'y ~ x1 + x2 + x3 - 1' линейная модель с тремя переменными без точки пересечения.
'y ~ x1 + x2 + x3 + x2^2' модель с тремя переменными с точкой пересечения и x2^2 термин.
'y ~ x1 + x2^2 + x3' совпадает с предыдущим примером, начиная с x2^2 включает x2 термин.
'y ~ x1 + x2 + x3 + x1:x2' включает x1*x2 термин.
'y ~ x1*x2 + x3' совпадает с предыдущим примером, начиная с x1*x2 = x1 + x2 + x1:x2.
'y ~ x1*x2*x3 - x1:x2:x3' имеет все взаимодействия среди x1x2 , и x3, кроме взаимодействия с тремя путями.
'y ~ x1*(x2 + x3 + x4)' имеет все линейные члены, плюс продукты x1 с каждой из других переменных.
Создайте использование подобранной модели fitglm или stepwiseglm. Выберите между ними, как в Выбирают Fitting Method и Model. Для обобщенных линейных моделей кроме тех с нормальным распределением дайте Distribution пара "имя-значение" как в Выбирает Generalized Linear Model и Link Function. Например,
mdl = fitglm(X,y,'linear','Distribution','poisson') % or mdl = fitglm(X,y,'quadratic',... 'Distribution','binomial')
После подбирания модели исследуйте результат.
Модель линейной регрессии показывает несколько диагностики, когда вы вводите ее имя или вводите disp(mdl). Это отображение дает часть основной информации, чтобы проверять, представляет ли подобранная модель данные соответственно.
Например, подбирайте модель Poisson к данным, созданным с два из пяти предикторов, не влияющих на ответ, и без термина точки пересечения:
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[.4;.2;.3]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson')
mdl =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x2 + x3 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.039829 0.10793 0.36901 0.71212
x1 0.38551 0.076116 5.0647 4.0895e-07
x2 -0.034905 0.086685 -0.40266 0.6872
x3 -0.17826 0.093552 -1.9054 0.056722
x4 0.21929 0.09357 2.3436 0.019097
x5 0.28918 0.1094 2.6432 0.0082126
100 observations, 94 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 44.9, p-value = 1.55e-08Заметьте, что:
Отображение содержит ориентировочные стоимости каждого коэффициента в Estimate столбец. Этими значениями является обоснованно около истинных значений [0;.4;0;0;.2;.3], кроме возможно коэффициента x3 не ужасно около 0.
Существует столбец стандартной погрешности для содействующих оценок.
pValue, о котором сообщают, (которые выведены из статистики t под предположением о нормальных ошибках) для предикторов 1, 4, и 5 малы. Это три предиктора, которые использовались, чтобы создать данные об ответе y.
pValue для (Intercept)x2 и x3 больше, чем 0,01. Эти три предиктора не использовались, чтобы создать данные об ответе y. pValue для x3 только по .05, так может быть расценен как возможно значительный.
Отображение содержит статистическую величину Хи-квадрата.
Диагностические графики помогают вам идентифицировать выбросы и видеть другие проблемы в вашей модели или подгонке. Чтобы проиллюстрировать эти графики, рассмотрите биномиальную регрессию с логистической функцией ссылки.
logistic model полезен для данных о пропорции. Это задает отношение между пропорцией p и весом w:
журнал [p / (1 – p)] = b 1 + b 2w
Этот пример подбирает биномиальную модель к данным. Данные выведены из carbig.mat, который содержит измерения больших автомобилей различных весов. Каждый вес в w имеет соответствующее количество автомобилей в total и соответствующее количество автомобилей плохого соотношения пройденного расстояния и расхода горючего в poor.
Разумно принять что значения poor следуйте за биномиальными распределениями с количеством испытаний, данных total и процент успехов в зависимости от w. Это распределение может составляться в контексте логистической модели при помощи обобщенной линейной модели с журналом функции ссылки (µ / (1 – µ)) = X b. Эта функция ссылки вызвана 'logit'.
w = [2100 2300 2500 2700 2900 3100 ... 3300 3500 3700 3900 4100 4300]'; total = [48 42 31 34 31 21 23 23 21 16 17 21]'; poor = [1 2 0 3 8 8 14 17 19 15 17 21]'; mdl = fitglm(w,[poor total],... 'linear','Distribution','binomial','link','logit')
mdl =
Generalized Linear regression model:
logit(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -13.38 1.394 -9.5986 8.1019e-22
x1 0.0041812 0.00044258 9.4474 3.4739e-21
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 242, p-value = 1.3e-54Смотрите, как хорошо модель соответствует данным.
plotSlice(mdl)
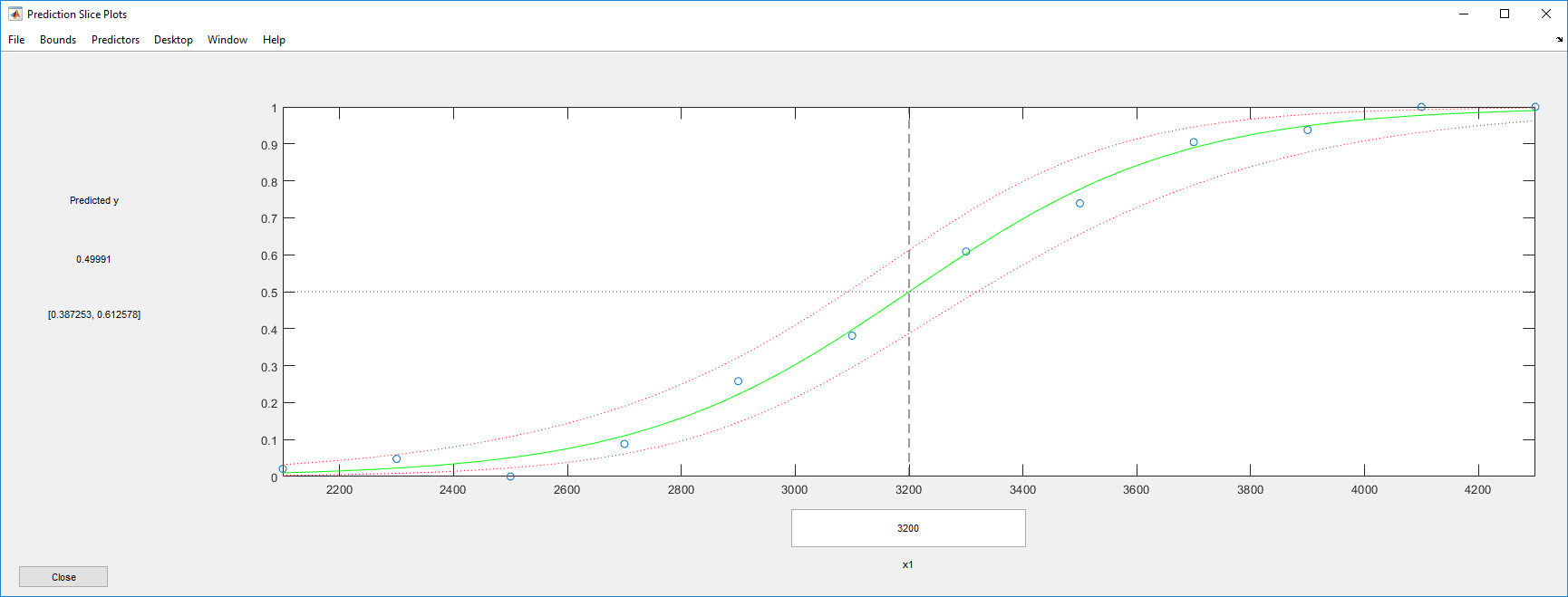
Подгонка выглядит довольно хорошей с довольно широкими доверительными границами.
Чтобы исследовать более подробную информацию, создайте график рычагов.
plotDiagnostics(mdl)
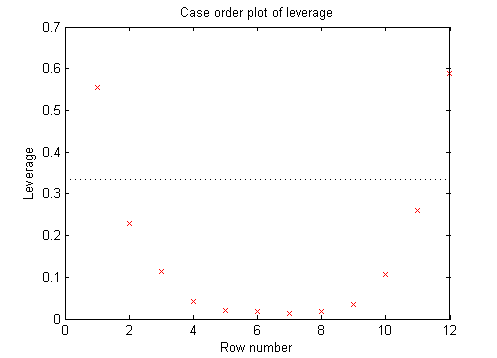
Это типично для регрессии с точками, упорядоченными переменным предиктором. Рычаги каждой точки на подгонке выше для точек с относительно экстремальными значениями предиктора (в любом направлении) и низко для точек со средними значениями предиктора. В примерах с несколькими предикторами и с точками, не упорядоченными значением предиктора, этот график может помочь вам идентифицировать, какие наблюдения имеют высокие рычаги, потому что они - выбросы, как измерено их значениями предиктора.
Существует несколько остаточных графиков помочь вам обнаружить ошибки, выбросы или корреляции в модели или данных. Самые простые остаточные графики являются графиком гистограммы по умолчанию, который показывает область значений остаточных значений и их частот и графика вероятности, который показывает, как распределение остаточных значений выдерживает сравнение с нормальным распределением с совпадающим отклонением.
Этот пример показывает остаточные графики для подбиравшей модели Poisson. Конструкция данных имеет два из пяти предикторов, не влияющих на ответ и никакой термин точки пересечения:
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson');
Исследуйте остаточные значения:
plotResiduals(mdl)
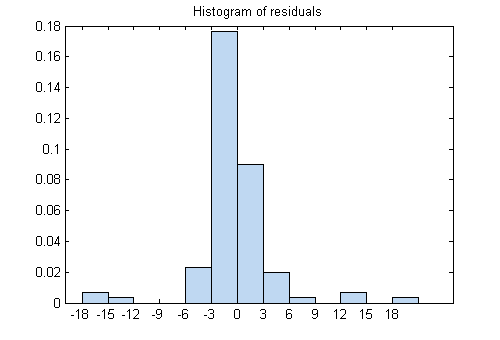
В то время как большая часть кластера остаточных значений около 0, существует несколько близких ±18. Поэтому исследуйте различный график остаточных значений.
plotResiduals(mdl,'fitted')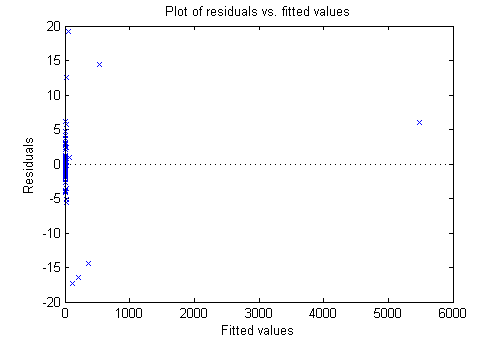
Большие остаточные значения, кажется, не имеют непосредственное отношение к размерам подходящих значений.
Возможно, график вероятности более информативен.
plotResiduals(mdl,'probability')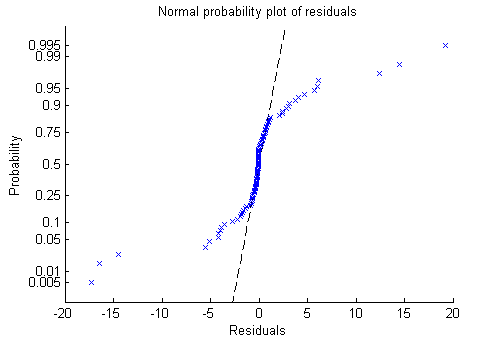
Теперь это ясно. Остаточные значения не следуют за нормальным распределением. Вместо этого у них более толстые хвосты как базовое распределение Пуассона.
В этом примере показано, как изучить эффект, каждый предиктор имеет на модели регрессии, и как изменить модель, чтобы удалить ненужные условия.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют вторые и третьи столбцы в X. Таким образом, вы ожидаете, что модель не покажет много зависимости от тех предикторов.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson');
Исследуйте график среза ответов. Это отображает эффект каждого предиктора отдельно.
plotSlice(mdl)

Шкала первого предиктора является подавляющей график. Отключите его с помощью меню Predictors.

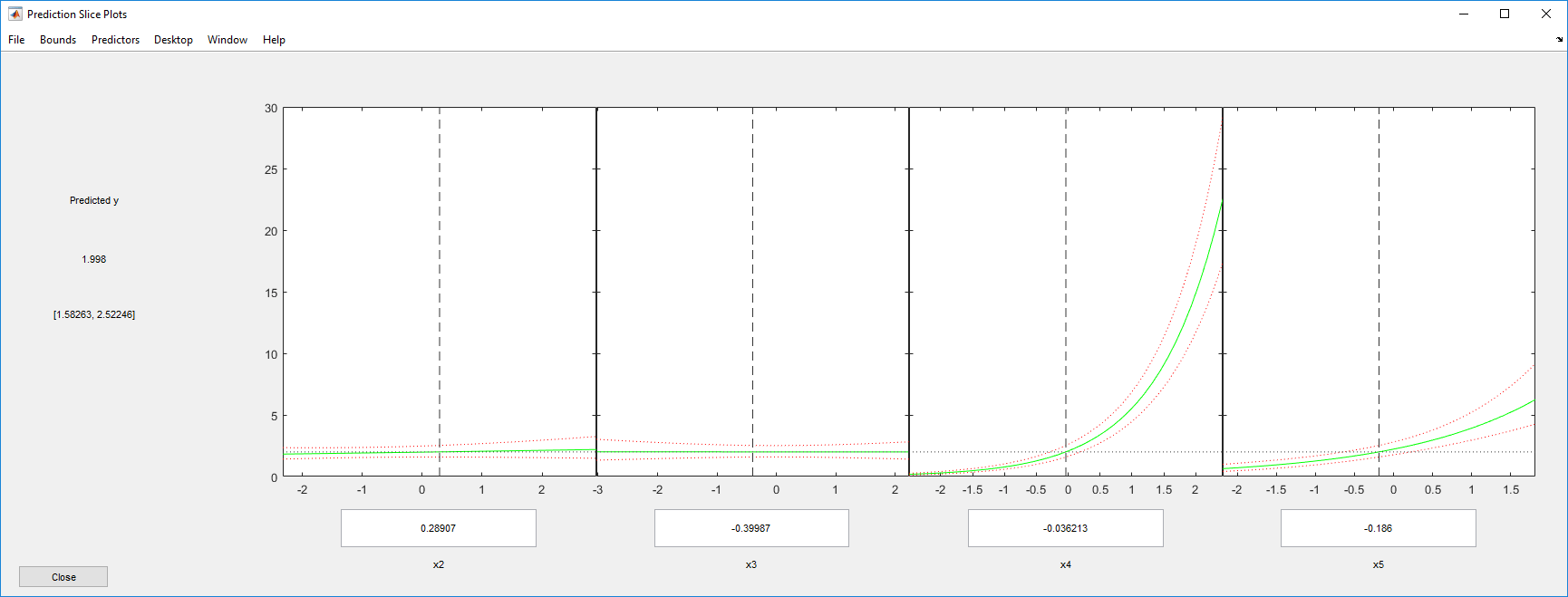
Теперь ясно, что предикторы 2 и 3 имеют мало бесцельно.
Можно перетащить отдельные значения предиктора, которые представлены пунктирными синими вертикальными линиями. Можно также выбрать между одновременными и неодновременными доверительными границами, которые представлены пунктирными красными кривыми. Перетаскивание линий предиктора подтверждает, что предикторы 2 и 3 имеют мало бесцельно.
Удалите ненужные предикторы с помощью любого removeTerms или step. Используя step может быть более безопасным, в случае, если существует неожиданная важность для термина, который становится очевидным после удаления другого термина. Однако иногда removeTerms может быть эффективным когда step не продолжает. В этом случае эти два дают идентичные результаты.
mdl1 = removeTerms(mdl,'x2 + x3')mdl1 =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0mdl1 = step(mdl,'NSteps',5,'Upper','linear')
1. Removing x3, Deviance = 93.856, Chi2Stat = 0.00075551, PValue = 0.97807
2. Removing x2, Deviance = 96.333, Chi2Stat = 2.4769, PValue = 0.11553
mdl1 =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0Существует три способа использовать линейную модель, чтобы предсказать ответ на новые данные:
predictpredict метод дает предсказание средних ответов и, если требуется, доверительные границы.
В этом примере показано, как предсказать и получить доверительные интервалы на предсказаниях с помощью predict метод.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют вторые и третьи столбцы в X. Таким образом, вы ожидаете, что модель не покажет много зависимости от этих предикторов. Создайте модель пошагово, чтобы включать соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data
[ynew,ynewci] = predict(mdl,Xnew)ynew =
1.0e+04 *
0.1130
1.7375
3.7471
ynewci =
1.0e+04 *
0.0821 0.1555
1.2167 2.4811
2.8419 4.9407fevalКогда вы создаете модель из таблицы или массива набора данных, feval часто более удобно для предсказания средних ответов, чем predict. Однако feval не обеспечивает доверительные границы.
В этом примере показано, как предсказать средние ответы с помощью feval метод.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют вторые и третьи столбцы в X. Таким образом, вы ожидаете, что модель не покажет много зависимости от этих предикторов. Создайте модель пошагово, чтобы включать соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); X = array2table(X); % create data table y = array2table(y); tbl = [X y]; mdl = stepwiseglm(tbl,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data ynew = feval(mdl,Xnew(:,1),Xnew(:,4),Xnew(:,5)) % only need predictors 1,4,5
ynew =
1.0e+04 *
0.1130
1.7375
3.7471Эквивалентно,
ynew = feval(mdl,Xnew(:,[1 4 5])) % only need predictors 1,4,5ynew =
1.0e+04 *
0.1130
1.7375
3.7471randomrandom метод генерирует новые случайные значения отклика для заданных значений предиктора. Распределение значений отклика является распределением, используемым в модели. random вычисляет среднее значение распределения от предикторов, оцененных коэффициентов и функции ссылки. Для распределений такой как нормальная, модель также обеспечивает оценку отклонения ответа. Для бинома и распределений Пуассона, отклонение ответа определяется средним значением; random не использует отдельную “дисперсионную” оценку.
В этом примере показано, как симулировать ответы с помощью random метод.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют вторые и третьи столбцы в X. Таким образом, вы ожидаете, что модель не покажет много зависимости от этих предикторов. Создайте модель пошагово, чтобы включать соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data
ysim = random(mdl,Xnew)ysim =
1111
17121
37457Предсказания от random выборки Пуассона, целые числа - также.
Оцените random метод снова, изменения результата.
ysim = random(mdl,Xnew)
ysim =
1175
17320
37126Отображение модели содержит достаточно информации, чтобы позволить кому-то еще воссоздать модель в теоретическом смысле. Например,
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson')
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0
2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0
3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
mdl =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0Можно получить доступ к описанию модели программно, также. Например,
mdl.Coefficients.Estimate
ans =
0.1760
1.9122
0.9852
0.6132mdl.Formula
ans = log(y) ~ 1 + x1 + x4 + x5
[1] Collett, D. Моделирование двоичных данных. Нью-Йорк: Chapman & Hall, 2002.
[2] Добсон, A. J. Введение в обобщенные линейные модели. Нью-Йорк: Chapman & Hall, 1990.
[3] Маккуллаг, P. и Дж. А. Нелдер. Обобщенные линейные модели. Нью-Йорк: Chapman & Hall, 1990.
[4] Neter, J., М. Х. Катнер, К. Дж. Нахцхайм и В. Вассерман. Прикладные линейные статистические модели, четвертый выпуск. Ирвин, Чикаго, 1996.