Документация

Непосредственные решатели

Первым шагом в вычислительном решении электромагнитных задач является дискретизация уравнений Максвелла. Процесс приводит к такой матрично-векторной системе:

Для вычисления матрицы взаимодействия и решения системных уравнений в панели инструментов антенны используется метод решателя моментов для металлических и диэлектрических структур.

Для вычисления поверхностных токов в структуре антенны сначала следует определить базовые функции Рао-Уилтона-Глиссона (RWG). Базисная функция RWG представляет собой пару треугольников, разделяющих ребро, и показана на рисунке.

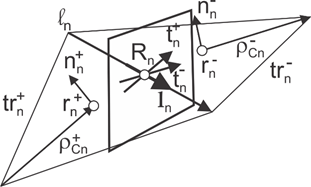
Для любых двух сегментов треугольника, $${}_{\mathrm{tn}}^{}$$+ и $${}_{}^{tn}$$−, имеющих $${\mathrm{области}}_{}^{}$$An + $${}_{и}^{}$$An −, и разделяющих общее $${}_{}$$ребро ln, базисной функцией является

и

Базисная функция равна нулю за пределами двух смежных треугольников $${}_{\mathrm{tn}}^{}$$+ и $${}_{}^{tn}$$−. Базисная функция вектора RWG является линейной и не имеет потока (нормальной составляющей) через ее границу.

Связь между используемой памятью и размером проблемы

Матрица Z взаимодействия является комплексной плотной симметричной матрицей. Это квадратная матрица N-на-N, где N - количество базисных функций, то есть количество внутренних рёбер в структуре. Рассмотрим сценарий большой конструкции типа самолета или корабля. Типичными узкополосными антеннами, такими как диполь или пластырь, являются полуволновые по размеру, но корабли или летательные аппараты часто могут иметь по меньшей мере 100 длин волн или больше по размеру. Для решения электромагнитных эффектов либо излучения, либо рассеяния от этой структуры с помощью полноволнового решателя первым шагом является создание сетки структуры, а затем формирование базовых функций. При этом генерируется более 50 000 треугольников. Так как потребность в памяти для прямого решателя составляет порядка O (^N2), в пространстве базисных функций рост показан на этом графике .

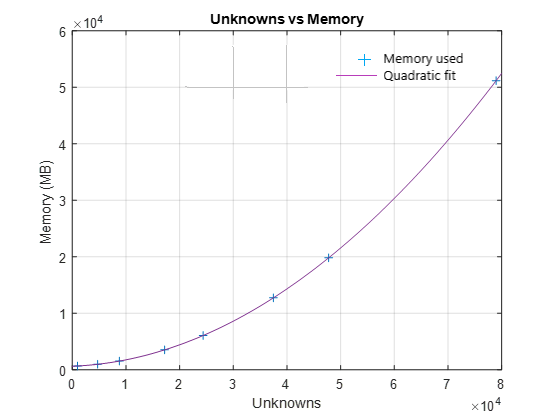
При любом из следующих условий число неизвестных становится очень большим:

Быстрый многопольный метод (FMM)

Ускорение, достигаемое алгоритмом FMM, обусловлено его способностью подразделять проблему на последовательно меньшие пространственные области, тем самым обеспечивая, чтобы взаимодействие между данной парой исходных и целевых кластеров было достаточно удаленным, чтобы его можно было вычислить с использованием многополюсных расширений. Следующий рисунок иллюстрирует это.

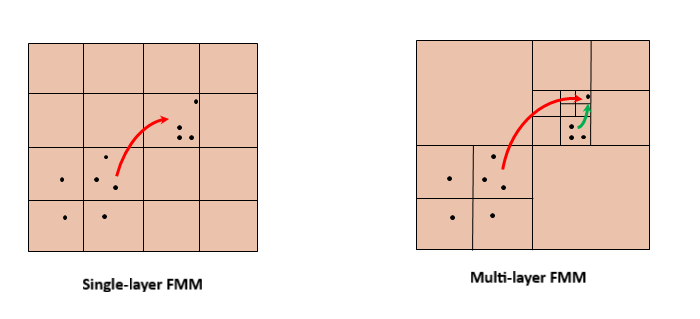
Этот подход хорошо согласуется с нашей необходимостью ускорить вычисление взаимодействий между разделенными парами базисных функций, то есть парами источника и целевого диполя. Задача определения электромагнитного потенциала в заданном наборе целевых точек в задаче Гельмгольца может быть выражена:

$$u(r){\displaystyle \underset{\mathrm{}}{\overset{}{}}{}_{}\frac{\mathrm{=\sum n=1Ncnexp}({}_{\mathrm{jk\; \text{'}r}}-}{rn{}_{|})}}{}_{}\frac{\mathrm{|r-rn|-vn·\nabla }({}_{\exp }(}{{\mathrm{jk\text{'}\; r}}_{}-}$$rn |) | r − rn |)

где cn _и vn _{представляют} совокупность уровней заряда и диполя, соответственно, k - волновое число, и u (r) - потенциал, вычисленный с помощью FMM в 3-D пространстве.

FMM ускоряет вычисление матрично-векторного произведения, существенно ускоряя вычисление двухточечных взаимодействий, опосредованных функцией Грина. Исходное распределение тока и заряда на поверхности мишени определяют введением этих коэффициентов обратно в расширение базисной функции. Затем определяют рассеянное или излучаемое поле цели, включая ее радиолокационные сечения, путем вычисления излучения известных поверхностных токов и зарядов в требуемых точках пространства. Итеративный подход к определению матрицы обратной - хорошо изученная и устоявшаяся область прикладной линейной алгебры. Среди множества существующих итеративных решателей метод обобщенного минимального остаточного (GMRES) является хорошо известным методом. На панели инструментов «Антенна» используется этот итеративный решатель.