Метод решателя моментов для металлических и диэлектрических структур

Методика вычисления моментов для металлических и диэлектрических антенн.

Антенны с использованием диэлектрической подложки состоят из металлической части и диэлектрической части. Первым шагом в вычислительном решении электромагнитных задач является дискретизация уравнений Максвелла. Процесс приводит к такой матрично-векторной системе:

$V =$ ZI

V - Вектор приложенного напряжения. Этот сигнал может представлять собой напряжение или мощность, подаваемые на антенну, или падающий на антенну падающий сигнал.
I - вектор тока, представляющий ток на поверхности антенны.
Z - матрица взаимодействия или матрица импеданса, которая соотносит V с I. Для вычисления матрицы взаимодействия влияние металлической и диэлектрической частей в антенне принимается отдельно.

Антенна Toolbox™ использует метод моментов (MoM) для вычисления матрицы взаимодействия и решения системных уравнений.

Состав протокола совещания

Состав MoM разделен на три части.

Дискретизация диэлектриков

Дискретизация дает возможность композиции от непрерывного домена к дискретному домену. Этот шаг называется наложением сетки в антенной литературе. В составе MoM металлическая поверхность антенны входит в треугольники, а диэлектрический объем - в тетраэдры.

Базовые функции

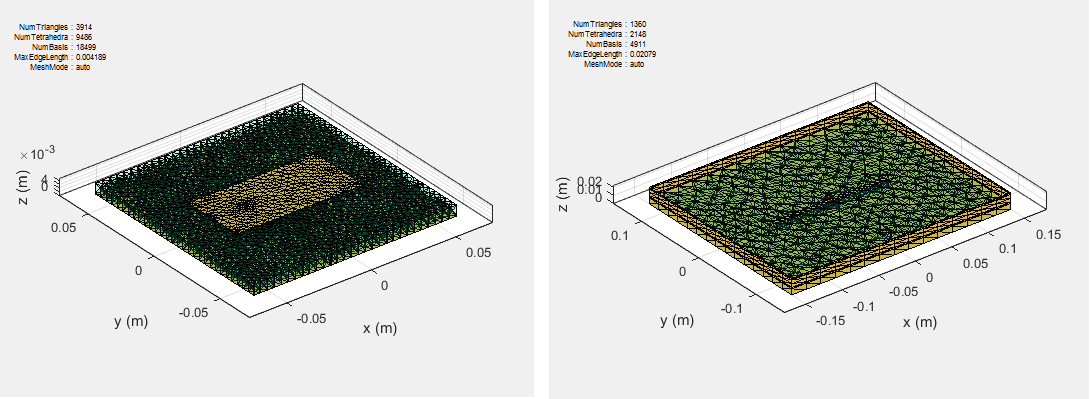
Базовые функции используются для представления неизвестных величин. В случае антенн, использующих диэлектрики, неизвестными величинами являются поверхностный ток на металлической структуре и плотность потока, обусловленная объемом диэлектрика. В Antenna Toolbox используются базовые функции Rao-Wilton-Glisson (RWG) [2]. Базовые функции для металлической конструкции в антенне см. в разделе Метод решателя моментов для металлических конструкций.

Для диэлектрического объема антенны Antenna Toolbox использует функцию базиса кромки нулевого порядка для моделирования плотности потока.

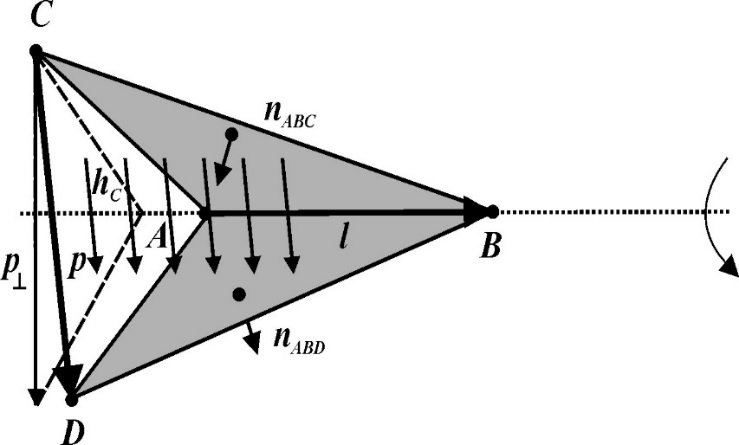
На рисунке показана базисная функция на основе границ. Вариация вектора перпендикулярна базовой кромке AB (или $\overset{}{l}$ ). Вектор рёберного CD (или $\overset{P)}{}$ определяет базисную функцию. В пределах тетраэдра базисная функция является постоянным полем, задаваемым

$\overset{}{} \overset{f\to=cp\to}{}$

c - коэффициент нормализации.
p - вектор ребра, определяющий базисную функцию.

Матрица взаимодействия

Матрица взаимодействия представляет собой комплексную плотную симметричную матрицу. Для металло-диэлектрической антенны существует два набора базисных функций и четыре взаимодействия. Чтобы заполнить матрицу взаимодействия, вычислите функцию Грина свободного пространства между всеми базисными функциями на поверхности антенны. Конечными матричными уравнениями взаимодействия являются:

Z_MM - взаимодействие металла с металлом. Для структуры из чистого металла вычисляется только эта симметричная квадратная матрица.
$_{}^{ZmnMM} = \frac{}{} \underset{}{(jωμ4π)} \underset{}{} {\overset{}{}}^{}_{} \overset{}{∫S∫Sf→Mm} (r {\overset{)}{\to}}^{.}_{} \overset{}{^{f\toMn}} (r \overset{}{{′→}^{)}} \overset{ГДР}{}'\to \frac{}{доктор →−} \underset{}{} \underset{}{} (j4πωε) {\overset{}{}}^{}_{∫S∫S} (\nabla {\overset{}{}}^{}_{.f→Mm}) (\overset{}{\nabla^{}} \overset{.f\toMn}{}$ ) ГДР ′→ доктор →
Z_DD - диэлектрическое к диэлектрическому взаимодействие. Для чистых диэлектрических структур вычисляется только эта симметричная квадратная матрица.
$\begin{array}{l} {\overset{}{}}_{}^{Z^mnDD} = \sum_{}^{}_{{p−1P∑p}^{}}^{^{}} \frac{_{}}{{\overset{}{}}_{}} \underset{_{}}{} {\overset{}{}}_{′−1P′Kpε^p∫VDf→mp} \overset{r}{(} \to) ⋅ {\overset{}{}}_{^{f\tonp}}' \overset{(}{} r \to \overset{}{)} \\ \frac{^{}_{}}{}_{}^{}_{^{}}^{^{}}_{}_{^{}} \underset{_{}}{} \underset{_{^{}}}{} доктор −ω2μ04π p−1P∑p −1PKpKp VDVDg \overset{r}{(} \to \overset{}{,^{r}}'\to {\overset{}{)}}_{} \overset{}{f→mp} (r {\overset{)}{\to}}_{^{}} \overset{'}{^{\cdotf\tonp}} (\overset{}{r} ′→ \overset{}{)^{}} \\ \frac{}{_{}}_{}^{}_{^{}}^{^{}} {\overset{}{}}_{} {\overset{}{}}_{^{}} \underset{_{}}{} \underset{_{^{}}}{} \overset{drdr -14πε0\sumq-1Qq -1Q'K^qK^q Ωq Ωq\intg}{} \vec{(^{r}}, r_{′→)} \overset{}{} {f⊥mq}_{(r^{\to}}) \overset{}{^{}} {f⊥nq}_{'}_{(^{r}} ′→) dsds ′ m, n=1 \end{array}$ ...., N
Z_MD и Z_DM - Эти матрицы вычисляют взаимодействие между металлом и диэлектриком. Эта матрица не является симметричной квадратной матрицей.
$\begin{array}{l} _{}^{} \frac{^{}_{}}{}_{}^{}_{^{}}^{^{}}_{} \underset{}{} \underset{_{^{}}}{} {\overset{}{}}_{}^{ZmnMD =−ω2μ04π p−12∑p −1P′Kp∫t∫VD′f→nM} \overset{r}{(} \to) ⋅ {\overset{}{}}_{^{f\tomp}}' \overset{r}{^{(}} ′→) \overset{g}{} \vec{(^{r}}, r \overset{)}{^{'\to}}_{} \\ \frac{}{_{}}_{}^{}_{}^{} {\overset{}{}}_{} \underset{_{}}{} \underset{_{^{доктор ds -14πε0\sump-12\sumq-1QK^q'tD Ωq }}}{} (_{} {\overset{}{}}_{}^{} \nablas\cdotf\tonM \overset{(}{} r \to_{))} \overset{}{^{f⊥mq}} (r \overset{)}{′→} \overset{(}{g^{}} r \to_{,^{r}}_{′→}) \\ dΩ ′ ds m=1 ....,_{} БЕЗ ОБОЗНАЧЕНИЯ ДАТЫ; n=1 ...,_{} \end{array}$ NM
$\begin{array}{l} _{}^{} \frac{_{}}{}_{}^{}_{^{}}^{^{}}_{^{}} \underset{_{}}{} \underset{_{^{}}}{} {\overset{}{}}_{ZmnDM =−jωμ04π p−12∑p −1PKp VDSDfnp} \overset{r}{(} \to) {\overset{}{}}_{}^{} \overset{(}{{⋅f→mM}^{}} r'\to \overset{}{)} g \overset{r}{^{(}} \to,_{r^{}} ′→ \overset{}{)} \\ ds′dr → \frac{}{_{}} {+14πε0ω}_{\sum}^{}_{}^{} {\overset{}{}}_{} \underset{_{}}{} \underset{_{^{}}}{}_{} p-12\sumq-1QK^q Ωq\intSDfnq \overset{(}{} r \to)_{\cdot} {\overset{}{(}}_{}^{} \overset{\nablas\cdotf\tomM}{^{}} (r \overset{)}{′→}) \overset{}{^{g}} (r_{\to^{,}} r_{} ′→) \\ ds'dΩ m=1_{....}, БЕЗ ОБОЗНАЧЕНИЯ ДАТЫ; n=1_{...} \end{array}$ , NM

где

$g \overset{}{(} \overset{}{^{}} r\to,r'\to) \frac{= \exp (-}{} jkR) \overset{}{} \overset{}{^{}}$ R,R=|r→−r′→| - функция Грина свободного пространства.
$K \frac{{\overset{}{=}}^{start^}_{}}{{\overset{}{\pm}}^{-}}$ α0, ^ ± - комплексная диэлектрическая постоянная внутри каждого тетраэдра.
${\overset{}{K}}_{^} q_{} =_{K}$ + − K − - дифференциальный контраст на каждой грани тетраэдра.

Для составной металлической структуры необходимо вычислить все четыре матрицы.

Соседний регион

На рисунке показана типичная матрица взаимодействия для металлической структуры. Z_MM с 256 базисными функциями.

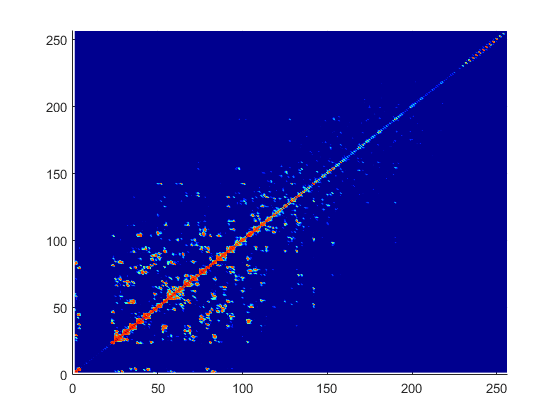
Из графика матрицы взаимодействия видно, что матрица является диагонально доминирующей. Матрица диэлектрического взаимодействия также является диагонально доминирующей. По мере удаления от диагонали величина членов уменьшается. Это поведение совпадает с поведением функции Грина. Функция Грина уменьшается по мере увеличения расстояния между r и r '. Поэтому важно точно вычислить область по диагонали и близко к диагонали.

Эта область на диагонали и вокруг нее называется соседней областью. Для металло-диэлектрической антенны область окрестности основана на среднем размере тетраэдра.

Сведения о соседних областях для металлических антенн см. в разделе Метод вычислителя моментов для металлических конструкций.

Извлечение сингулярности

По диагонали r и r 'идентичны, и определенная функция Грина становится единственной. Для удаления сингулярности на этих условиях производится извлечение. Уравнения для извлечения сингулярности Z_MM матричные:

$\begin{array}{l} \underset{_{}}{} \underset{_{∫tp∫tq}}{} {\overset{}{(}}_{} {\overset{}{}}^{}_{} ρ\toi.ρ\to'j) \overset{}{г} (\overset{}{^{}} r→,r′→) \underset{_{}}{} \underset{_{}}{} \frac{{\overset{}{}}_{ds'ds=∫tp∫tq} {\overset{}{(}}^{}_{}}{\overset{}{} ρ\toi.ρ\to'j \overset{}{)^{}}} \underset{_{}}{} \underset{_{}}{} \frac{|r\to-r'\to|ds'ds+\inttp\inttq (\overset{exp}{} \overset{}{(^{}} {\overset{}{}}_{−jk'r→−r′→|}) {\bar{}}^{}_{1})}{\overset{}{(} \overset{}{^{}}} ρ→i.ρ→′j) \\ \underset{_{}}{} \underset{_{}}{} \overset{}{} \overset{}{^{}} |r→−r′→|ds'ds∫tp∫tqg (\underset{_{}}{} \underset{_{r→,r′→}}{} \frac{)}{\overset{}{} \overset{}{^{}}} \underset{_{}}{} \underset{_{}}{} \frac{\overset{}{} \overset{}{^{ds'ds=\inttp\inttq1|r\to-r'\to|ds'ds+\inttp\inttq}} (exp}{(\overset{}{} \overset{}{^{}}} −jk'r→−r′→|) \end{array}$ − 1) |r→−r′→|ds'ds

Два интеграла в правой части уравнений, называемые потенциальными или статическими интегралами, находят с помощью аналитических результатов [3].

Уравнения для извлечения сингулярности Z_DD матричные:

$\begin{array}{l} \underset{_{}}{} \underset{_{^{}}}{} ∫VD∫VD′g \overset{}{(} \overset{}{^{}} r\to,r'\to) \overset{}{} \overset{}{^{}} \underset{_{}}{} \underset{_{}}{} \frac{}{\overset{}{} \overset{}{^{}}} \overset{}{} \overset{}{^{}} \underset{_{}}{} \underset{_{}}{} \frac{dr→dr′→=∫VD∫Vq1|r→−r′→|dr→dr′→+∫VD∫Vq (\exp (\overset{}{} \overset{}{^{}} -jk'r\to-r'\to|}{) \bar{} \overset{}{1^{)}}} \overset{}{} \overset{}{^{}} \\ \underset{_{}}{} \underset{_{^{}}}{} \overset{}{} \overset{|r\to-r'\to|dr\todr'\to\intΩq\intΩq'g}{^{}} (\underset{)_{}}{r\to,r'\to} \underset{_{}}{} \frac{}{\overset{}{} \overset{}{^{}}} \underset{_{}}{} \underset{_{}}{} \frac{dΩdΩ'=\intΩD\intΩq1|r\to-r'\to|dΩdΩ'+\intSD\intSq \overset{(}{} \overset{}{^{exp}} (}{\overset{}{} \overset{-jk'r\to-r'\to|}{^{}})} - 1 \end{array}$ ) |r→−r′→|dΩdΩ

Конечные массивы

Формулировка MoM для конечных решеток такая же, как для одного антенного элемента. Основное отличие - количество возбуждений (кормов). Для конечных массивов вектор напряжения теперь является матрицей напряжения. Количество столбцов равно количеству элементов в массиве.

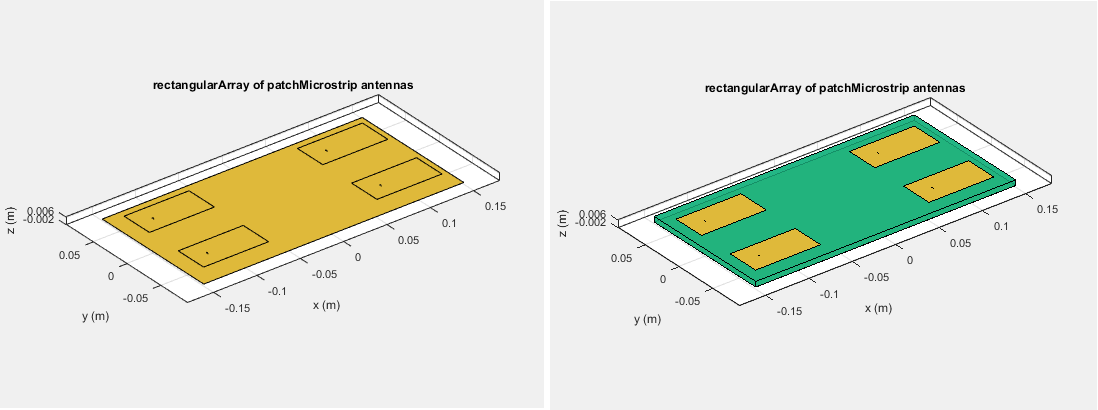
Например, матрица вектора напряжения для 2x2 решетка прямоугольной коммутационной антенны (с диэлектрической подложкой и без нее) имеет четыре столбца, так как каждая антенна может возбуждаться отдельно.

Бесконечный массив

Чтобы смоделировать бесконечный массив, измените MoM, чтобы учесть бесконечное поведение. Для этого следует заменить функции Грина со свободным пространством периодическими функциями Грина. Периодическая функция Грина является бесконечным двойным суммированием.

Функция Грина	Функция периодического зеленого
$\begin{array}{l} \frac{^{}}{} \\ \overset{}{} {\overset{}{}}^{} g=e-jkRRR=\|r\to-r\to'\| \end{array}$	$\begin{array}{l} _{gperiodic} = \sum_{m}^{}_{}^{}^{_{}} \frac{^{_{}}}{_{}} \\ _{=− n =− ejϕmne−jkRmnRmnRmn} = \sqrt{{(^{x-x}_{}'-xm}^{)} {2 + (^{} {y−y}_{}}^{}'-yn {) 2 +^{} (}^{}} \\ _{z−z'}) 2ϕmn =_{−k} (_{} xmsinθcosφ + \\ _{} ynsinθsinφ) xm_{} =m⋅dx,_{}_{} \end{array}$ yn=n⋅dy

Функция Грина

Функция периодического зеленого

$\begin{array}{l} \frac{^{}}{} \\ \overset{}{} {\overset{}{}}^{} g=e-jkRRR=|r\to-r\to'| \end{array}$

$\begin{array}{l} _{gperiodic} = \sum_{m}^{}_{}^{}^{_{}} \frac{^{_{}}}{_{}} \\ _{=− n =− ejϕmne−jkRmnRmnRmn} = \sqrt{{(^{x-x}_{}'-xm}^{)} {2 + (^{} {y−y}_{}}^{}'-yn {) 2 +^{} (}^{}} \\ _{z−z'}) 2ϕmn =_{−k} (_{} xmsinθcosφ + \\ _{} ynsinθsinφ) xm_{} =m⋅dx,_{}_{} \end{array}$ yn=n⋅dy

dx и dy - размеры нулевой плоскости, определяющие размеры x и y единичной ячейки. λ и Λ - углы сканирования.

Сравнивая две функции Грина, можно наблюдать дополнительный экспоненциальный член, который добавляется к бесконечной сумме. Для сканирования бесконечного массива используется _{файл Фmn}. Функция периодического Грина также учитывает эффект взаимной связи.

Дополнительные сведения см. в разделе Бесконечные массивы.

Ссылки

[1] Харрингтон, Р. Ф. Полевые вычисления методом момента. Нью-Йорк: Макмиллан, 1968.

[2] Рао, С. М., Д. Р. Уилтон и А. В. Глиссон. «Электромагнитное рассеяние по поверхностям произвольной формы». IEEE. Пер. антенны и распространение, т. AP-30, № 3, май 1982, стр. 409-418.

[3] Уилтон, Д. Р., С. М. Рао, А. В. Глиссон, Д. Х. Шобер, О. М. Аль-Бундак. и К. М. Батлер. «Потенциальные интегралы для равномерного и линейного распределения источников на полигональных и многогранных доменах». IEEE. Передние антенны и распространение. Т. AP-30, № 3, 1984 мая, с. 276-281.

[4] Баланис, К. А. Теория антенн. Анализ и проектирование. 3-й ред. Нью-Йорк: Джон Уайли и сыновья, 2005.

Документация