Гибридный метод вычисления моментов (MoM) физической оптики (PO) в Antenna Toolbox™ позволяет моделировать антенны вблизи больших рассеивателей, таких как параболические отражатели. Антенный элемент моделируется с использованием МоМ, в то время как влияние электрически больших структур рассматривается с использованием РО.
Знакомые базовые функции Рао Уилтона Глиссона (RWG) на треугольниках основаны на [2].
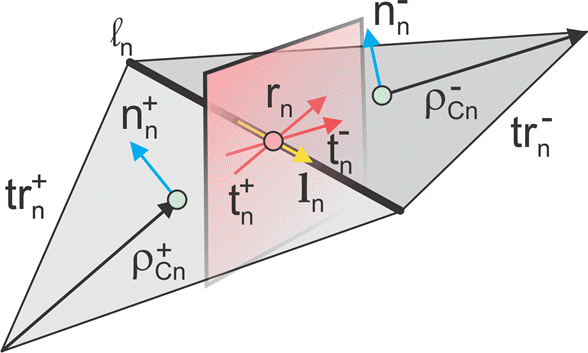
В изображении для двух произвольных треугольных патчей trn + и trn-, имеющих области An + и An- и совместно использующих общий край ln, базовые функции имеют вид
где - вектор, выводимый из свободной вершины треугольника trn + в точку наблюдения r→; ρ→n−=r→n−−r→ - вектор, выводимый из точки наблюдения в свободную вершину треугольника. Базисная функция равна нулю за пределами двух смежных треугольников. Базисная функция вектора RWG является линейной и не имеет потока (то есть не имеет нормальной составляющей) через свою границу.
Из [1], наряду со стандартным определением, этот метод требует двух единичных нормальных векторов и двухблочных векторов, также показано на рисунке. Вектор - плоскость треугольника trn +; оба вектора перпендикулярны краю ln. Они определяются в центре ребра, которое обозначается . Направления
также показаны на рисунке. Этот метод предполагает, что нормальные векторы являются правильными (угол между соседними должен быть меньше 180 градусов) и однозначно определены. Конкретная векторная ориентация (например, внешний или внутренний нормальные векторы) не имеет значения. Затем мы формируем два перекрестных вектора продуктов ,
и установить, что оба таких единичных вектора, направленных вдоль края, идентичны,
В конечном итоге необходим только векторный l→n.
Плотность поверхностного тока ) на всей поверхности металла расширена на N базисных функций RWG. Однако часть таких базисных функций принадлежит региону MoM (или «точному региону»), в то время как другая часть будет принадлежать региону PO (или «приблизительному региону»). Эти базовые функции (или области) могут перекрываться и произвольно распределяться в пространстве (не обязательно быть смежными). Метод предполагает, что базис NMoM функционирует от области MoM до в списке, а базис NPO для области PO после этого. Следовательно, имеется = N)
Если нет области заказа на поставку, можно решить всю проблему, используя MoM с одной квадратной матрицей ^ системы MoM, которая может быть разделена на 4 матрицы, как показано.
)
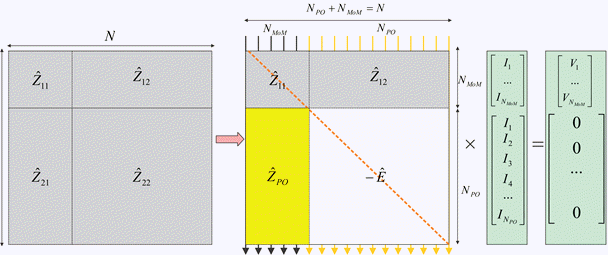
На рисунке показана матричная интерпретация гибридного решения MoM-PO и его сравнение с простым решением MoM. Способ предполагает, что антенное питание дает вектор, , описывающий возбуждение, которое принадлежит только области MoM.
Гибридное решение сохраняет подматрицы 11 ^ 12. Другими словами, способ решает стандартную систему линейных уравнений для области MoM, где рассматривается излучение из области PO через Z ^ 12.
Гибридное решение полностью игнорирует подматрицы Z 22. Здесь токи в области PO не взаимодействуют друг с другом. Их находят через излучаемое магнитное поле r→) из области МоМ с помощью аппроксимации ПО [1]. Новая матрица описывает эту ^ PO и отрицательную единичную матрицу E, которая Z ^ 22.
Подходящая аппроксимация заказа на поставку имеет вид [1]
где δ учитывает эффекты затенения. Если точка наблюдения находится в области тени, δ должно быть равно нулю. В противном случае он равен ± 1 в зависимости от направления падения относительно вектора нормали ориентации r→). Использование второго экв. (4) дает:
Ссылка [1] описывает элегантный способ явного выражения неизвестных InPO с использованием интересного варианта метода коллокации. Сначала рассмотрим точку коллокации, которая стремится к центру ребра определенной базисной функции ) и находится в его треугольнике плюс. Затем умножаем Eq. (7) на вектор t→n+NMoM+. Поскольку нормальный компонент интересующей базисной функции на ребре является одним, а все остальные базисные функции, совместно использующие тот же треугольник, не имеют нормального компонента на этом ребре, результат становится
Повторите ту же операцию с треугольником минус и получите
Добавьте оба Eqs. (8a) и (8b) вместе, разделить результат на два и преобразовать тройное векторное произведение для получения
Поэтому, согласно Eqs. (2) и (3),
Для завершения деривации H-поле, излучаемое областью MoM, всегда записывается в виде
где ) даются отдельными базовыми функциональными вкладами. В простейшем случае каждый такой вклад - это дипольное излучение [3]. Замена экв. (11) на экв. (10) дает
Согласно второму рисунку, спаренная система уравнений имеет вид
Метод прямого решения приводит к замене выражения для тока PO в первом уравнении,
Примечание
Классическая формула физической оптики (РО) не поддерживает множественные отражения от физической структуры, освещенной плоской волной. Плотность тока PO действительна только в освещенной области конструкции. Эта композиция не обрабатывает какие-либо отражения от освещенной области, которые приводят к вторичному освещению другой области структуры.
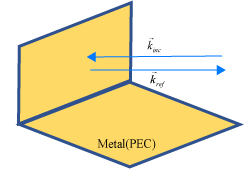
Случай 1: Когда направление падающей плоской волны приводит к отражению назад в направлении входящего источника.
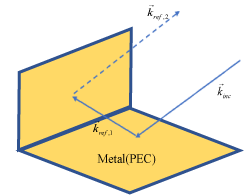
Случай 2: Когда угол падающей плоской волны вызывает второе отражение от другой части структуры, это отражение вносит значительный вклад в рассеянное поле и не учитывается решателем PO.
.
[1] У. Джакобус и Ф. М. Ландсторфер, «Улучшенная рецептура PO-MM для рассеяния из трехмерных идеально проводящих тел произвольной формы», IEEE Trans. Antennas and Propagation, vol. AP-43, no. 2, pp. 162-169, Febr.1995.
[2] С. М. Рао, Д. Р. Уилтон и А. В. Глиссон, «Электромагнитное рассеяние по поверхностям произвольной формы», IEEE Trans. Antennas and Propagation, vol. AP-30, no. 3, pp. 409-418, май 1982.
[3] С. Макаров, Моделирование антенн и ЕМ в MATLAB, Вайли, Нью-Йорк, 2002.