Бесконечные массивы

Что такое бесконечные массивы?

Бесконечные массивы - прямоугольные массивы бесконечной протяженности. В бесконечном массиве один элемент, называемый единичной ячейкой, повторяется равномерно бесконечное число раз вдоль плоскости.

Бесконечный анализ массива

Все массивы, используемые в реальных сценариях, являются конечными. Но антенные решетки, используемые в радиоастрономии, ПВО или радарах наблюдения, могут иметь более 1000 антенных элементов. В таких больших массивах электромагнитный анализ каждого элемента является утомительным и трудоемким.

Бесконечный анализ массива игнорирует эффект усечения (эффект ребра) на ребрах массива. Способ анализирует поведение активного антенного элемента как функцию частоты и сканирования. Целью бесконечного анализа решетки является извлечение поведения активного антенного элемента, внедренного в решетку.

Предположения

Для бесконечного анализа массива размер массива должен быть больше 10x10. Методика делает другие предположения:

Каждый элемент идентичен.
Каждый элемент равномерно возбуждается по амплитуде.
Все элементы равномерно разнесены в двух измерениях.

Решатель бесконечных массивов

Для моделирования бесконечного массива метод формулирования моментов (MoM) изменяется, чтобы учесть бесконечное поведение путём замены функций Грина периодическими функциями Грина. Периодическая функция Грина является бесконечным двойным суммированием.

Функция Грина	Функция периодического зеленого
$\begin{array}{l} \frac{^{}}{} \\ \overset{}{} {\overset{}{}}^{} g=e-jkRRR=\|r\to-r\to'\| \end{array}$	$\begin{array}{l} _{gperiodic} = \sum_{m}^{}_{}^{}^{_{}} \frac{^{_{}}}{_{}} \\ _{=− n =− ejϕmne−jkRmnRmnRmn} = \sqrt{{(^{x-x}_{}'-xm}^{)} {2 + (^{} {y−y}_{}}^{}'-yn {) 2 +^{} (}^{}} \\ _{z−z'}) 2ϕmn =_{−k} (_{} xmsinθcosφ + \\ _{} ynsinθsinφ) xm_{} =m⋅dx,_{}_{} \end{array}$ yn=n⋅dy

Функция Грина

Функция периодического зеленого

$\begin{array}{l} \frac{^{}}{} \\ \overset{}{} {\overset{}{}}^{} g=e-jkRRR=|r\to-r\to'| \end{array}$

$\begin{array}{l} _{gperiodic} = \sum_{m}^{}_{}^{}^{_{}} \frac{^{_{}}}{_{}} \\ _{=− n =− ejϕmne−jkRmnRmnRmn} = \sqrt{{(^{x-x}_{}'-xm}^{)} {2 + (^{} {y−y}_{}}^{}'-yn {) 2 +^{} (}^{}} \\ _{z−z'}) 2ϕmn =_{−k} (_{} xmsinθcosφ + \\ _{} ynsinθsinφ) xm_{} =m⋅dx,_{}_{} \end{array}$ yn=n⋅dy

_dx и _dy - размеры нулевой плоскости, определяющие размеры x и y единичной ячейки. λ и Λ - углы сканирования.

Функция периодического Грина имеет дополнительный экспоненциальный член, добавляемый к бесконечной сумме. Член _Фmn учитывает сканирование бесконечного массива. Функция периодического Грина также учитывает эффект взаимной связи.

Создание бесконечной решетки с помощью панели инструментов антенны

Чтобы создать бесконечный массив, используйте infiniteArray объект для повторения одного антенного элемента (единичной ячейки), бесконечно вдоль плоскости X-Y. layout функция отображает типовую единичную ячейку.

infarray = infiniteArray;
layout(infarray)

Выбор единичной ячейки

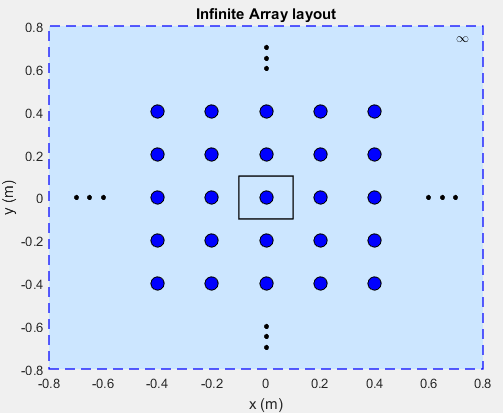
В качестве единичной ячейки можно использовать любую антенну из Toolbox™ антенн. Для задания границ единичной ячейки требуется заземляющая плоскость. Для задней антенны, не имеющей нулевой плоскости, можно использовать отражатель.

Свойства отражателя по умолчанию:

r = reflector

 reflector with properties:

              Exciter: [1x1 dipole]
    GroundPlaneLength: 0.2000
     GroundPlaneWidth: 0.2000
              Spacing: 0.0750
                 Tilt: 0
             TiltAxis: [1 0 0]

Единичная ячейка по умолчанию в бесконечной матрице является отражателем, который имеет диполь в качестве возбудителя. Spacing свойство задает расстояние между отражателем и возбудителем. Свойства бесконечного массива по умолчанию:

infarray = infiniteArray

 infiniteArray with properties:

          Element: [1x1 reflector]
      ScanAzimuth: 0
    ScanElevation: 90

show (infarray)

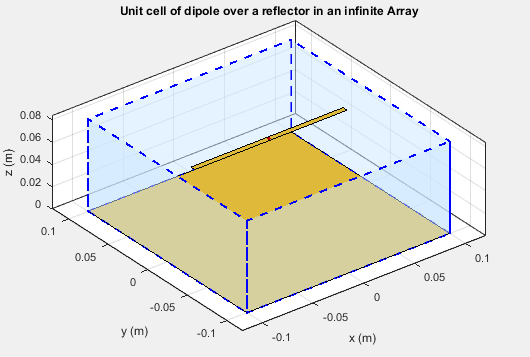
Пунктирная синяя рамка ограничивает единичную ячейку. Длина плоскости заземления и ширина плоскости заземления единичной ячейки - размеры антенного элемента бесконечной решетки.

Антенна с нулевой плоскостью, такая как микрополосковая коммутационная антенна, задается непосредственно как Element бесконечного массива.

infarray = infiniteArray('Element', patchMicrostrip)

infarray = 
  infiniteArray with properties:

          Element: [1x1 patchMicrostrip]
      ScanAzimuth: 0
    ScanElevation: 90

show(infarray)

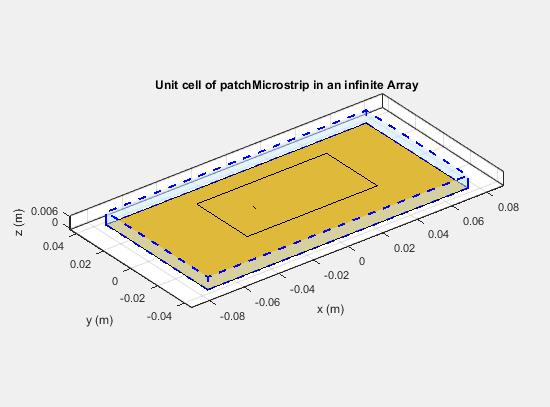
Бесконечная решетка Antenna Toolbox расположена в плоскости X-Y. В плоскости X-Y также расположены единичные ячейки, состоящие из антенн с плоскостями заземления. Для антенн, используемых в качестве единичных ячеек, например в данном примере, игнорируется значение Tilt собственность.

Сканировать бесконечные массивы

Вы сканируете конечную решетку, указывая соответствующий фазовый сдвиг для каждого антенного элемента. В окне «Панель инструментов антенны» задается угол сканирования (по азимуту и отметке) и частота для анализа бесконечной решетки. По умолчанию массив всегда сканируется в точке ближнего визирования (азимут = 0 градусов и отметка = 90 градусов).

infarray = infiniteArray

 infiniteArray with properties:

          Element: [1x1 reflector]
      ScanAzimuth: 0
    ScanElevation: 90

Для изменения углов обзора измените значения ScanAzimuth и ScanElevation.

Полное сопротивление сканирования и шаблон элемента сканирования

Чтобы вычислить полное сопротивление сканирования для бесконечного массива, используйте impedance функция как функция угла обзора. Фиксация пары углов сканирования и сдвиг частотной переменной показывает зависимость частоты в импедансе сканирования. Поскольку ScanAzimuth и ScanElevation являются скалярными значениями, необходимо использовать for- петля, чтобы вычислить полный импеданс просмотра множества. Дополнительные сведения о расчете полного сопротивления сканирования и шаблона элемента сканирования см. в разделе Анализ бесконечных массивов.

Образец элемента сканирования

Чтобы вычислить шаблон элемента сканирования с помощью импеданса сканирования, используйте следующие выражения:

$_{gs} (start) \frac{=_{}_{}_{} 4RgRisogiso}{{(_{start}) |_{Zs}}^{(}}$ start) + Zg | 2

Rg - Сопротивление генератора
Zg - импеданс генератора
Zs - полное сопротивление сканирования
giso (start) - Образец изолированного элемента
Riso - сопротивление изолированного элемента

Рисунок элемента сканирования также может быть выражен в терминах коэффициента отражения Γ (λ):

$_{gs} (λ) \frac{=_{}_{} 4Risogiso}{_{(} start)} Rs ({λ) (1}^{−}$ | Γ (λ) | 2)

Программа Antenna Toolbox вычисляет схему элементов сканирования конечной решетки, управляя только одним элементом. Все остальные элементы завершаются с использованием соответствующего импеданса. Результирующая структура элемента включает взаимное соединение и действительна для всех углов сканирования.

Сравнение массива элементов сканирования конечных и бесконечных массивов

Случай 1: Сравните конечный массив и бесконечный массив с единичной ячейкой размерностей 0.5λ × 0.5λ

Чтобы вычислить структуру элементов сканирования конечных массивов, сначала создайте диполь с отражателем. Задайте для размеров диполя $значение Length (L) =$ 0,495λ $и Width (W) =$ λ/160, а для размеров нулевой плоскости - значение 0.5λ × 0.5λ. Разместите диполь на расстоянии h = λ/4 от отражателя. Размеры нулевой плоскости задают границы единичной ячейки. Создание конечных массивов размеров11x11, 15x15, и 17x17 с использованием этой единичной ячейки.

Для конечных массивов вычислите шаблон элемента сканирования, управляя одним элементом в массиве. Завершите все другие конечные элементы массива, используя широкополосное сопротивление бесконечного массива. Для бесконечного массива с единичной ячейкой размерностей 0,5λ × 0,5λ широкополосное сопротивление составляет 176 Λ. Вычислите образец элемента сканирования для E-, D- и H-плоскостей всех трех конечных массивов.

Чтобы вычислить массив элементов сканирования бесконечного массива, создайте бесконечный массив, используя ту же единичную ячейку и infiniteArray класс. Вычислите полное сопротивление сканирования для трех плоскостей сканирования: E, D и H. Вычислите рисунок изолированного элемента (диполя, поддерживаемого отражателем). Наконец, используйте уравнения из предыдущего раздела, чтобы создать шаблон элемента сканирования для бесконечного массива.

Выполните весь анализ с частотой 10 ГГц. Чтобы сравнить узоры конечного и бесконечного массивов, наложите их на один и тот же график.

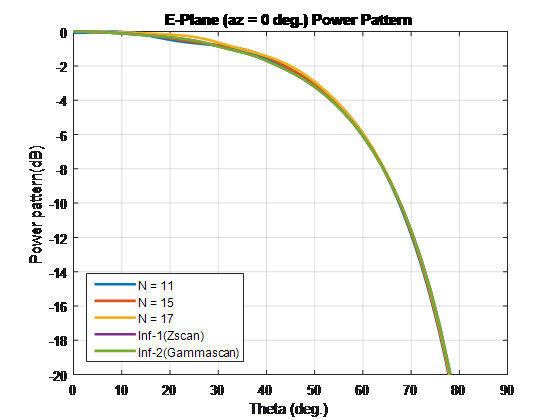
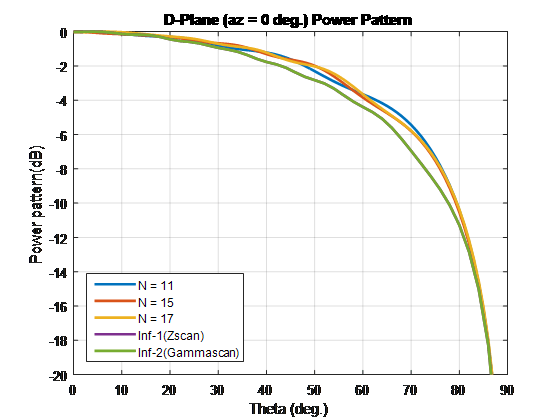
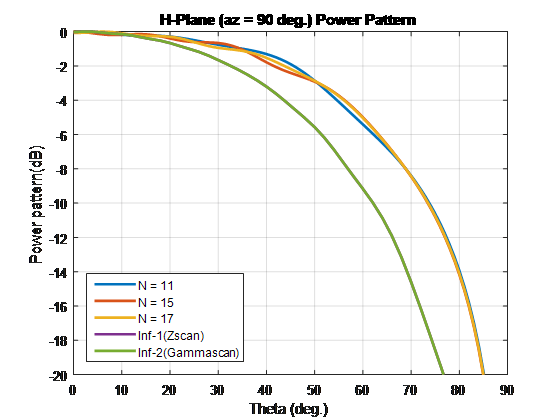
Случай 2: Сравните конечный массив и бесконечный массив с единичной ячейкой размеров 0.7λ × 0.7λ

Для сравнения массива элементов сканирования этих типов и бесконечных массивов повторите процесс в случае 1. С помощью этих размеров единичной ячейки создаются лепестки решетки. Завершите конечные массивы, используя сопротивление 86-Ω. Для бесконечного массива с единичной ячейкой размерностей 0,7λ × 0,7λ широкополосное сопротивление составляет 86 Λ.

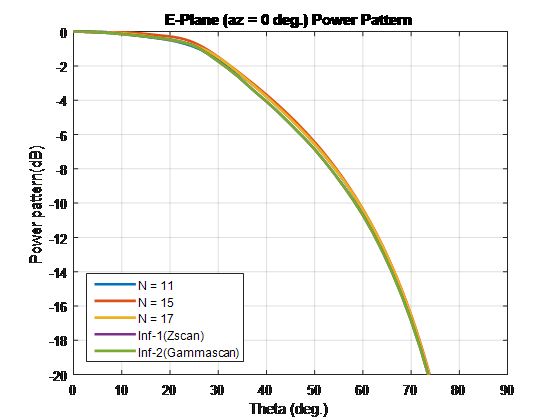
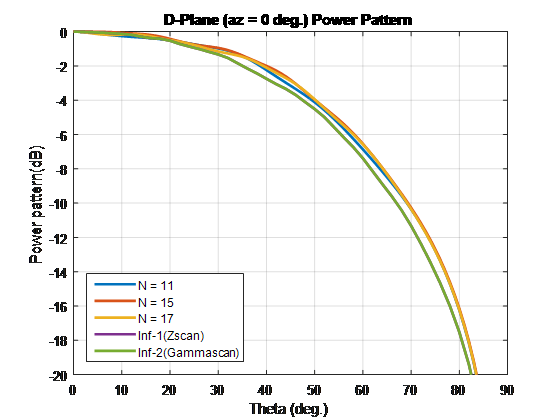
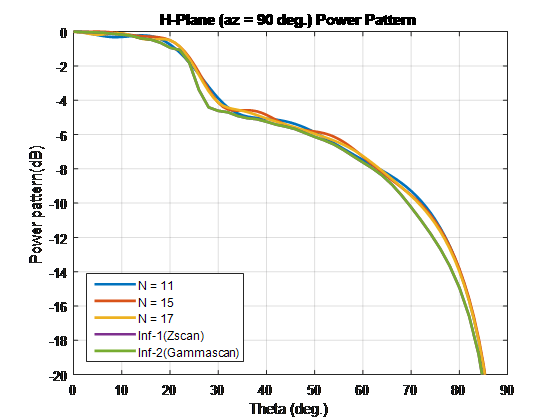
Для конечных массивов размером более 10 x 10 шаблоны элементов сканирования в плоскостях E-, D- и H соответствуют шаблонам бесконечного элемента сканирования массива.

Влияние бесконечного двойного суммирования

Как показано в уравнениях Грина, функция периодического Грина имеет бесконечное двойное суммирование в (m, n). При выполнении бесконечного анализа массива количество членов в двойном суммировании влияет на точность конечного решения. Большее количество терминов приводит к лучшей точности, но увеличивает время вычислений.

По умолчанию используется панель инструментов антенны 10 члены для каждого члена суммирования (m, n) для выполнения бесконечного анализа массива. Общая длина члена суммирования составляет 2 * 10 + 1 (-10 к +10). Чтобы изменить количество терминов, используйте метод numSummationTerms.

Большее количество терминов требуется, если:

Наблюдаются отрицательные значения сопротивления сканирования для определенных углов сканирования на определенных частотах.
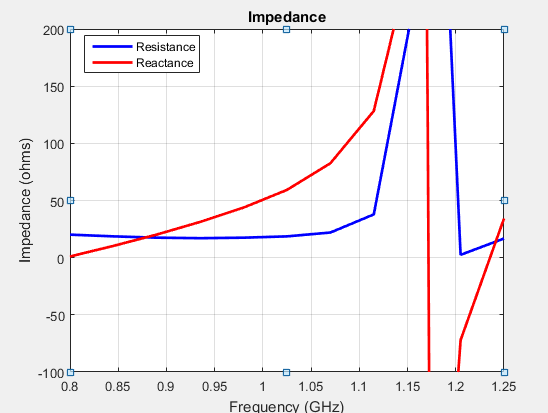
Необходимо исследовать сходимость, когда импеданс сканирования показывает медленные изменения.

Ссылки

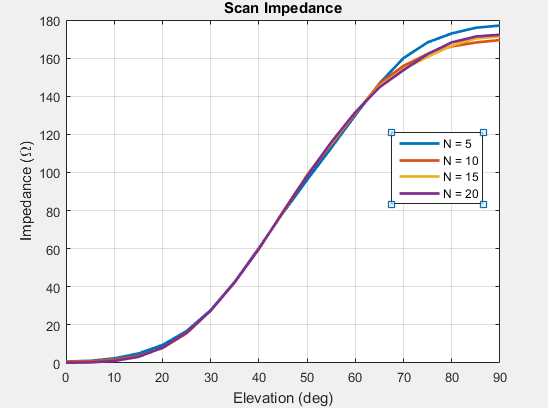
[1] Майю, Р. Дж. Руководство по фазированной антенной решетке. Норвуд, Массачусетс: Артех Хаус. 2-е издание. 2005.

[2] Хансен, R.C. Фазированные антенные решетки. Хобокен, Нью-Джерси: John Wiley & Sons Inc. 2-е издание. 1998, стр 221–313.

[3] Аллен, J. «Изменение усиления и импеданса в сканируемых дипольных массивах». Транзакции IRE на антеннах и распространение. Том 10, номер 5, сентябрь 1962, стр. 566-572.

[4] Васылківський, У., и У. Кан. «Эффективность как мера размера фазированной антенной решетки». Транзакции IEEE на антеннах и распространении. Том 21, номер 6, ноябрь 1973, стр. 879-884.

[5] Holter, H. и Х. Стеискэл. «О требовании к размеру для моделей с конечной фазированной решеткой». Транзакции IEEE на антеннах и распространении. Том 50, номер 6, июнь 2002 года, стр. 836-840.

Документация