Документация

Решатель проводов

Ниже приведено сокращенное описание выведения уравнений, решаемых решателем проводов. Для получения более подробной информации см. [1].

Для проводников PEC (Perfect electric conducting) граничные условия требуют, чтобы тангенциальная составляющая общего электрического поля на поверхности провода была равна нулю:

Можно также выразить уравнение в терминах плотности поверхностного тока, $${\stackrel{}{}}_{\mathrm{J\to s}}$$, на проводе PEC и его пространственной производной. Это делается путем интегрирования эффекта поверхностной плотности тока с использованием функции Грина, $$g(\stackrel{}{}{\stackrel{}{}}^{}|r\to -r\to \text{'}|$$). Функция Грина абстрактно представляет влияние бесконечно малого источника поверхностно-токовой плотности, расположенного в $${\stackrel{}{}}^{r\to }$$ 'на электрическое и магнитное поля в точке наблюдения $$\stackrel{}{}$$r→. Функция Грина для распространения свободного пространства:

где $$k=\sqrt{{}_{\mathrm{}}{}_{\mathrm{}}}$$startα0pci0 - волновое число, а λ - угловая частота. В общем, для решения электромагнитной (ЭМ) проблемы и получения ЭМ полей в среде необходимы следующие шаги. Для точного представления ЭМ-проблемы на поверхности провода принимаются во внимание как продольные, так и поперечные компоненты интегрированного тока и требуется, чтобы величина (1) поддерживалась по всей поверхности провода. Дискретизируйте Eq. (1) над конечным множеством точек или базисных функций, чтобы получить множество уравнений. Дискретизируйте поверхностную плотность тока в конечное множество базисных функций, чтобы получить множество неизвестных. Решите набор уравнений неизвестных, чтобы получить дискретное приближение к поверхностным токам-плотностям на проводе. Эти плотности тока позволяют вычислять электромагнитные поля в любой требуемой точке. Для тонких проводов указанные выше шаги являются исчерпывающими и упрощают функцию Green для:

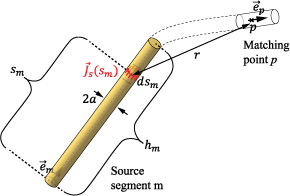
где $${}_{\mathrm{ra}}\sqrt{{=}^{\mathrm{}}{\mathrm{r2}}^{\mathrm{}}}$$+ a2 - приблизительное среднее $$\stackrel{расстояния}{}{\stackrel{}{}}^{}$$|r→−r→'|, r - расстояние между бесконечно малым поверхностным источником плотности тока и осью провода, a - радиус провода. Кроме того, плотность тока на проводе заменяется $$\mathrm{}{\stackrel{}{}}_{}$$I=2πa'J→s|| тока провода. Используя вышеприведенное приближение, запишите Eq. (1) как:

где s - продольное положение вдоль провода, а $$\stackrel{e\to }{}(ы$$) - единичный вектор, представляющий ориентацию провода в этом положении. Дискретизируйте провод в конечное число сегментов s (m), где m =1....N, а затем дополнительно дискретизировать Eq. (4) в конечное множество уравнений, наложенных в точках, соответствующих p =1....N для получения:

где _Im (_sm) - распределение тока вдоль сегмента m, аппроксимируемое многочленом вида:

где _hm - длина сегмента и _nm - выбранная степень полинома (которая отличается от сегмента к сегменту). Подставляя Eq. (6) в (5), набор уравнений может быть записан в матричном формате как:

где [_{Zp, mi}] - матрица импеданса, [_Imi] - вектор неизвестных коэффициентов, представляющих ток на проводе, и [_Vexp, p] - вектор возбуждения. Более подробная информация о расчете элементов _[Zp, mi] приведена в [ 1].