Уравнивание

Уравнивание (EQ) - это процесс взвешивания частотного спектра звукового сигнала.

Выравнивание можно использовать для:

Улучшение аудиозаписей
Анализ спектрального содержания

Типы уравнивания включают в себя:

Фильтры нижних и верхних частот - ослабляют высокочастотное и низкочастотное содержимое соответственно.
Низкосортные и высокосортные эквалайзеры - Boost или отсекающие частоты одинаково выше или ниже желаемой точки отсечения.
Параметрические эквалайзеры - выборочное увеличение или сокращение частотных диапазонов. Также известен как пиковые фильтры.
Графические эквалайзеры - выборочно увеличивать или сокращать октавные или дробные октавные полосы частот. Полосы имеют основанные на стандартах центральные частоты. Графические эквалайзеры являются частным случаем параметрических эквалайзеров.

В этом учебном пособии описывается, как Audio Toolbox™ реализует функции проектирования: designParamEQ, designShelvingEQ, и designVarSlopeFilter. multibandParametricEQ Система object™ объединяет функции проектирования фильтров в многополосный параметрический эквалайзер. graphicEQ Системный объект объединяет функции проектирования фильтров и octaveFilter Системный объект для стандартного графического выравнивания. Учебное пособие, посвященное использованию функций проектирования в MATLAB ®, см. в разделе Проектирование параметрического эквалайзера.

Проектирование уравнивания с использованием панели инструментов «Звук»

Тип эквалайзера и расчетные параметры Примеры откликов по величине

Тип эквалайзера и расчетные параметры	Примеры откликов по величине
Использовать `designVarSlopeFilter` для создания фильтров нижних и верхних частот. Расчетные параметры `designVarSlopeFilter` включают: Нормированная частота отсечки Наклон (дБ/октава)	Lowpass	Highpass
Использовать `designShelvingEQ` для создания низкополочных и высокополочных эквалайзеров Расчетные параметры `designShelvingEQ` включают: Коэффициент усиления (дБ) Нормированная частота отсечки Наклон (дБ/октава)	Нижние полки	Высокая полка
Использовать `designParamEQ` для создания параметрических эквалайзеров. Можно создать однополосные параметрические эквалайзеры или каскад параметрических эквалайзеров. Использование каскада параметрических эквалайзеров позволяет точно настроить частотную характеристику. Расчетные параметры `designParamEQ` включают: Количество диапазонов эквалайзера Коэффициент усиления (дБ) Нормализованная полоса пропускания Нормированная центральная частота Порядок фильтрации	Параметрический эквалайзер	Каскад параметрических выравнивателей

Использовать designVarSlopeFilter для создания фильтров нижних и верхних частот.

Расчетные параметры designVarSlopeFilter включают:

Нормированная частота отсечки
Наклон (дБ/октава)

Lowpass

Highpass

Использовать designShelvingEQ для создания низкополочных и высокополочных эквалайзеров

Расчетные параметры designShelvingEQ включают:

Коэффициент усиления (дБ)
Нормированная частота отсечки
Наклон (дБ/октава)

Нижние полки

Высокая полка

Использовать designParamEQ для создания параметрических эквалайзеров. Можно создать однополосные параметрические эквалайзеры или каскад параметрических эквалайзеров. Использование каскада параметрических эквалайзеров позволяет точно настроить частотную характеристику.

Расчетные параметры designParamEQ включают:

Количество диапазонов эквалайзера
Коэффициент усиления (дБ)
Нормализованная полоса пропускания
Нормированная центральная частота
Порядок фильтрации

Параметрический эквалайзер

Каскад параметрических выравнивателей

Проектирование фильтра EQ

Функции проектирования Audio Toolbox используют метод билинейного преобразования конструкции цифрового фильтра для определения коэффициентов эквалайзера. В методе билинейного преобразования:

Выберите аналоговый прототип.
Укажите параметры конструкции фильтра.
Выполните билинейное преобразование.

Прототип аналоговой полки

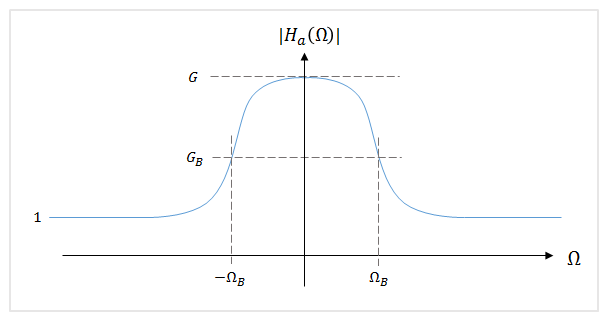
Audio Toolbox использует дизайн параметрического эквалайзера высокого порядка, представленный в [1]. В этом методе проектирования аналоговый прототип рассматривается как низкополочный фильтр Баттерворта:

$_{Ха} (ы) {\frac{}{}}^{}_{}^{} \frac{^{}^{}_{}^{}}{^{}_{}^{}}$ =[gβ+sβ+s]r∏i=1L[g2β2+2gsiβs+s2β2+2siβs+s2]

$• L$ = Количество аналоговых секций SOS

$• N$ = Порядок аналоговых фильтров

$• r = \begin{matrix} {0 N \\ even1 N нечетный \end{matrix}$

$• g =^{}$ G1/N

$• β =_{} {StartB \sqrt{\frac{^{×} (_{}^{G2}}{_{−}^{}}}}^{\frac{}{GB2GB2}} − 1) \frac{-}{} 1N {= \sqrt{\frac{^{} \tan_{}^{(}}{_{}^{} πΔω2)}}}^{\times \frac{}{(}}$ G2 − GB2GB2 − 1) − 1N, где Δ

$•_{si} = \frac{sin ((2i}{−} 1) security2N), i =$ 1,2,..., L

Для параметрических эквалайзеров аналоговый прототип уменьшается путем установки коэффициента усиления полосы пропускания в квадратный корень пикового коэффициента усиления (GB = sqrt (G)).

После задания конструктивных параметров аналоговый прототип преобразуется непосредственно в нужный цифровой эквалайзер полосовым билинейным преобразованием:

$s \frac{= 1 -_{} 2cos^{(} λ 0)^{z}}{-^{1}}$ + z − 21 − z − 2

_{λ 0} - требуемая цифровая центральная частота.

Это преобразование удваивает порядок фильтрации. Каждая аналоговая секция первого порядка становится цифровой секцией второго порядка. Каждая аналоговая секция второго порядка становится цифровой секцией четвертого порядка. Audio Toolbox всегда вычисляет цифровые секции четвертого порядка, что означает, что возврат секций второго порядка требует вычисления корней и менее эффективен.

Цифровые коэффициенты

Функция цифровой передачи реализована в виде каскада секций второго и четвертого порядка.

$H (z) {\frac{_{}_{}^{}_{}^{}}{_{}^{}_{}^{}}}^{}_{}^{} \frac{_{}_{}^{}_{}^{}_{}^{}_{}^{}}{_{}^{}_{}^{}_{}^{}_{}^{}}$ =[b00+b01z−1+b02z−21+a01z−1+a02z−2]r∏i=1L[bi0+bi1z−1+bi2z−2+bi3z−3+bi4z−41+ai1z−1+ai2z−2+ai3z−3+ai4z−4]

Коэффициенты задаются путем выполнения полосового билинейного преобразования на аналоговом прототипе.

Коэффициенты сечения второго порядка	Коэффициенты секции четвертого порядка
$\begin{array}{l} _{D0} = β \\ _{+} 1b00 = (1_{} \\ +_{} gβ) /_{D0b01} =_{−} \\ _{} 2cos (λ 0) /_{} \\ _{} D0b02 = (1 -_{} gβ_{)} \\ /_{} D0a01 = -_{} \end{array}$ 2cos (λ 0 )/D0a02 = (1 − β )/ D0	$\begin{array}{l} _{Di} =^{} β2_{+} \\ _{2siβ} +^{}^{1bi0} = (_{} g2β2 +_{} \\ _{} 2gsiβ +_{1}) /_{} Dibi1 =_{} \\ -_{} 4c0 (1 +^{} {gsiβ}_{}) /^{}^{} Dibi2 =_{} \\ 2_{(} 1 +_{} 2cos2_{(} ü 0)_{-} \\ _{} g2β2^{)} /^{} {Dibi3}_{} = −_{4c0} \\ _{(1} -_{} gsiβ)_{/}_{Dibi4} \\ _{=} (g2β2 - 2β2 -^{}_{2g}^{}_{} \\ _{}_{}_{}_{} \\ _{}^{}_{}_{} \end{array}$

Коэффициенты сечения второго порядка

Коэффициенты секции четвертого порядка

$\begin{array}{l} _{D0} = β \\ _{+} 1b00 = (1_{} \\ +_{} gβ) /_{D0b01} =_{−} \\ _{} 2cos (λ 0) /_{} \\ _{} D0b02 = (1 -_{} gβ_{)} \\ /_{} D0a01 = -_{} \end{array}$ 2cos (λ 0 )/D0a02 = (1 − β )/ D0

$\begin{array}{l} _{Di} =^{} β2_{+} \\ _{2siβ} +^{}^{1bi0} = (_{} g2β2 +_{} \\ _{} 2gsiβ +_{1}) /_{} Dibi1 =_{} \\ -_{} 4c0 (1 +^{} {gsiβ}_{}) /^{}^{} Dibi2 =_{} \\ 2_{(} 1 +_{} 2cos2_{(} ü 0)_{-} \\ _{} g2β2^{)} /^{} {Dibi3}_{} = −_{4c0} \\ _{(1} -_{} gsiβ)_{/}_{Dibi4} \\ _{=} (g2β2 - 2β2 -^{}_{2g}^{}_{} \\ _{}_{}_{}_{} \\ _{}^{}_{}_{} \end{array}$

Биквадратичный случай. В биквадратическом случае, когда N = 1, коэффициенты уменьшаются до:

$\begin{array}{l} _{D0} \frac{=_{}}{\sqrt{}} StartBG \\ _{+} 1b00_{=} \sqrt{} (1_{+}_{StartBG})/ D0,_{} b01 =_{} -_{} 2cos ({start0}_{} \sqrt{})/_{D0} \\ ,_{} b02 = (1_{−}_{StartBG}) /_{} D0a01 \frac{=_{}}{\sqrt{-}}_{} \end{array}$ 2cos (start0 )/ D0, a02 = (1 − StartBG )/ D0

Денормализация коэффициента a00 и выполнение замен A = sqrt (G) $,_{}$ ΩB≅α дает привычные пиковые коэффициенты EQ, описанные в [2].

Орфанидис отмечает аппроксимативную эквивалентность в [1]

Используя тригонометрические идентичности,

$_{StartB} = \frac{\tan}{(} Δω2) =_{} sin (λ 0 \frac{)}{} sinh ($ ln22B),

где B играет роль эквивалентной октавной полосы пропускания.

Бристоу-Джонсон получил приблизительное решение для B в [4]:

$B \frac{=_{}}{_{}} start0sinü 0$ × BW

Подстановка аппроксимации для B в уравнение StartB даёт определение $α$ в [2]:

$α = \sin_{} \frac{}{} \frac{_{}}{_{}}$ (

Проектирование фильтра нижних и верхних частот

Прототип аналоговой полки

Для проектирования фильтров нижних и верхних частот в Audio Toolbox используется специальный случай конструкции фильтра для параметрических эквалайзеров. В этой конструкции пиковый коэффициент усиления G устанавливается равным 0, а GB2 устанавливается равным 0,5 (отсечение -3 дБ). Частота отсечки фильтра нижних частот соответствует 1 - StartB. Частота отсечки фильтра верхних частот соответствует

Цифровые коэффициенты

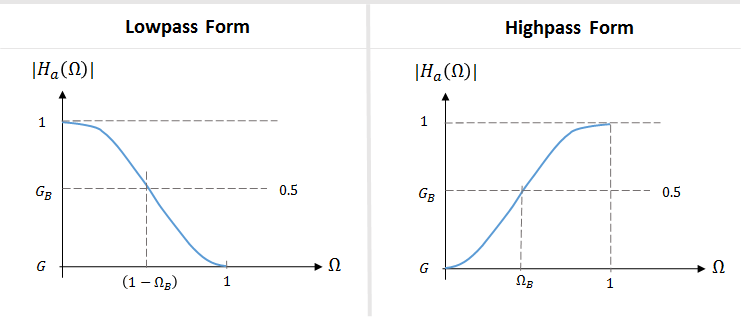
В таблице обобщены результаты полосового билинейного преобразования. Для фильтров нижних частот и 0 для фильтров верхних частот задают цифровую центральную частоту λ 0.

Коэффициенты секции второго порядка	Коэффициенты секции четвертого порядка
$\begin{array}{l} _{} \frac{}{} \\ _{}_{} \\ _{} {B00=1/D0b01 =−2cos D0=1+tan (πΔω2)}_{}_{(ω0)} \\ _{}_{} \\ _{}_{} /d0b02=1/d0a01 =-2cos_{} \\ _{(ω0)} /D0a02 = (\frac{}{} 1-tan_{} \end{array}$ (πΔω2))/D0	$\begin{array}{l} _{}^{} \frac{}{} Di=tan2 (πΔω2)_{} +2sitan \frac{}{} \\ {(πΔω2)}_{}_{} \\ _{}_{} +1bi0=1/Dibi1 =-4cos_{} \\ _{(ω0)} {/Dibi2=2}^{(}_{} {1+2cos2}_{} \\ _{} (ω0)) {_{}}_{}_{} \\ {/dibi3 =−4cos}_{} (ω0)_{} \\ _{}_{}_{} 0/Dibi4=1/Diai1 =−4cos \frac{(ω0)}{} (_{} \\ _{1+sitan} {(πΔω2))}^{}_{} {/Diai2=2}^{(} \frac{}{} 1+2cos2_{} \\ _{(ω0)} −tan2_{} (πΔω2))_{} \frac{}{} /diai3 =-4cos_{} \\ _{(ω0)} (^{} \frac{1−sitan}{}_{(πΔω2)}) \frac{}{/Diai4} = (_{tan2} \end{array}$ (πΔω2) −2sitan (πΔω2) +1)/Di

Коэффициенты секции второго порядка

Коэффициенты секции четвертого порядка

$\begin{array}{l} _{} \frac{}{} \\ _{}_{} \\ _{} {B00=1/D0b01 =−2cos D0=1+tan (πΔω2)}_{}_{(ω0)} \\ _{}_{} \\ _{}_{} /d0b02=1/d0a01 =-2cos_{} \\ _{(ω0)} /D0a02 = (\frac{}{} 1-tan_{} \end{array}$ (πΔω2))/D0

$\begin{array}{l} _{}^{} \frac{}{} Di=tan2 (πΔω2)_{} +2sitan \frac{}{} \\ {(πΔω2)}_{}_{} \\ _{}_{} +1bi0=1/Dibi1 =-4cos_{} \\ _{(ω0)} {/Dibi2=2}^{(}_{} {1+2cos2}_{} \\ _{} (ω0)) {_{}}_{}_{} \\ {/dibi3 =−4cos}_{} (ω0)_{} \\ _{}_{}_{} 0/Dibi4=1/Diai1 =−4cos \frac{(ω0)}{} (_{} \\ _{1+sitan} {(πΔω2))}^{}_{} {/Diai2=2}^{(} \frac{}{} 1+2cos2_{} \\ _{(ω0)} −tan2_{} (πΔω2))_{} \frac{}{} /diai3 =-4cos_{} \\ _{(ω0)} (^{} \frac{1−sitan}{}_{(πΔω2)}) \frac{}{/Diai4} = (_{tan2} \end{array}$ (πΔω2) −2sitan (πΔω2) +1)/Di

Конструкция фильтра для стеллажей

Аналоговый прототип

Audio Toolbox реализует конструкцию фильтра-полки, представленную в [2]. В данной конструкции аналоговые прототипы высокой и низкой полок представлены отдельно:

$_{HL} (s) = \frac{A^{} (\frac{\sqrt{}}{As2} + (}{^{AQ}) \frac{\sqrt{s}}{} +} 1s2 + ({AQ}_{)} s + A \frac{)^{} HH \frac{\sqrt{}}{(} s) =}{A^{} (\frac{\sqrt{s2}}{} + (} AQ$ ) s + AAs2 + (AQ) s + 1)

Для компактности аналоговые фильтры представлены переменными A и Q. Можно преобразовать A и Q в доступные параметры конструкции Audio Toolbox:

$\begin{array}{l} A =^{} \\ \frac{}{} \sqrt{10G/401Q = \frac{}{(} A \frac{+}{1A)} (} \end{array}$ 1скат − 1) + 2

После задания параметров конструкции аналоговый прототип преобразуется в требуемый цифровой фильтр-полку билинейным преобразованием с предварительной обработкой:

$s = \frac{(z}{-} 1z \frac{+}{1) \frac{\times_{}}{(}}$ 1тан (λ 02))

Цифровые коэффициенты

В таблице суммированы результаты билинейного преобразования с предварительной обработкой.

Нижние полки	Высокая полка	Промежуточные переменные
$\begin{array}{l} _{} b0=A ((A+1) − (A−1)_{}, потому что \sqrt{} (ω0) \\ _{} +2αA) b1=2A ((A-1) -_{} \\ _{(A+1)}, потому что (ω0)) b2=A (_{} (A+1) − \sqrt{} \\ _{} (A-1), потому что (ω0) -2αA)_{} a0 = \sqrt{} \\ _{} (A+1) + (A-1), потому что (ω0)_{} \\ _{} +2αAa1 =-2 ((A−1) +_{} (A+1) \sqrt{, потому что} \end{array}$ (ω0)) a2 = (A+1) + (A−1), потому что (ω0) −2αA	$\begin{array}{l} _{} b0=A ((A+1) + (A−1)_{}, потому что \sqrt{} (ω0) \\ _{} +2αA) b1 =-2A ((A−1) +_{} \\ _{(A+1)}, потому что (ω0)) b2=A (_{} (A+1) + \sqrt{} \\ _{} (A-1), потому что (ω0) -2αA)_{} a0 = \sqrt{} \\ _{} (A+1) - (A-1), потому что {(ω0)}_{} \\ _{} +2αAa1=2 ((A−1) +_{} (A+1) \sqrt{, потому что} \end{array}$ (ω0)) a2 = (A+1) − (A−1), потому что (ω0) −2αA	$\begin{array}{l} α \frac{= \sin_{} (}{} \sqrt{λ 0) \frac{2}{} (A \frac{}{+ 1A)} (} \\ _{1slope} − \frac{1) + 2Aω0 =}{} \end{array}$ 2πCutoff FrequencyF

Нижние полки

Высокая полка

Промежуточные переменные

$\begin{array}{l} _{} b0=A ((A+1) − (A−1)_{}, потому что \sqrt{} (ω0) \\ _{} +2αA) b1=2A ((A-1) -_{} \\ _{(A+1)}, потому что (ω0)) b2=A (_{} (A+1) − \sqrt{} \\ _{} (A-1), потому что (ω0) -2αA)_{} a0 = \sqrt{} \\ _{} (A+1) + (A-1), потому что (ω0)_{} \\ _{} +2αAa1 =-2 ((A−1) +_{} (A+1) \sqrt{, потому что} \end{array}$ (ω0)) a2 = (A+1) + (A−1), потому что (ω0) −2αA

$\begin{array}{l} _{} b0=A ((A+1) + (A−1)_{}, потому что \sqrt{} (ω0) \\ _{} +2αA) b1 =-2A ((A−1) +_{} \\ _{(A+1)}, потому что (ω0)) b2=A (_{} (A+1) + \sqrt{} \\ _{} (A-1), потому что (ω0) -2αA)_{} a0 = \sqrt{} \\ _{} (A+1) - (A-1), потому что {(ω0)}_{} \\ _{} +2αAa1=2 ((A−1) +_{} (A+1) \sqrt{, потому что} \end{array}$ (ω0)) a2 = (A+1) − (A−1), потому что (ω0) −2αA

$\begin{array}{l} α \frac{= \sin_{} (}{} \sqrt{λ 0) \frac{2}{} (A \frac{}{+ 1A)} (} \\ _{1slope} − \frac{1) + 2Aω0 =}{} \end{array}$ 2πCutoff FrequencyF

Ссылки

[1] Орфанидис, Софокл Дж. «Дизайн цифрового параметрического эквалайзера высокого порядка». Журнал Общества аудиотехники. том 53, ноябрь 2005, стр. 1026-1046.

[2] Бристоу-Джонсон, Роберт. «Формулы cookbook для коэффициентов фильтра Biquad аудио EQ». Доступ состоялся 02 марта 2016 года. http://www.musicdsp.org/files/Audio-EQ-Cookbook.txt.

[3] Орфанидис, Софокл Дж. Введение в обработку сигналов. Энглвуд Клиффс, Нью-Джерси: Прентис Холл, 2010.

[4] Бристоу-Джонсон, Роберт. «Эквивалентность различных методов вычисления коэффициентов биквада для параметрических уравнивателей звука». Представлен на 97-м съезде АЕС, Сан-Франциско, ноябрь 1994 года, AES Preprint 3906.

См. также

designParamEQ | designShelvingEQ | designVarSlopeFilter | graphicEQ | multibandParametricEQ

Документация