Оценка коэффициентов памяти-полинома для цифровой предыскаженности
Панель инструментов связи/Коррекция нарушений RF
Оценка коэффициентов памяти-полинома для цифровой предыскажения (DPD) нелинейного усилителя мощности.
Этот значок показывает блок со всеми включенными портами.
Типы данных |
|
Многомерные сигналы |
|
Сигналы переменного размера |
|
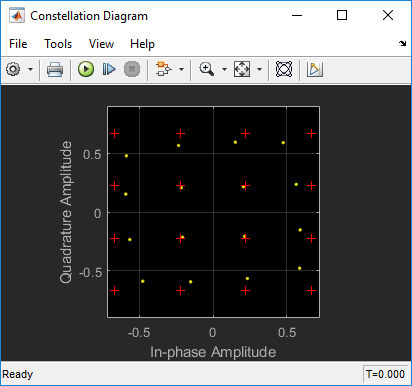
Передачи беспроводной связи обычно требуют передачи сигнала с широкой полосой пропускания в широком динамическом диапазоне сигналов. Для передачи сигналов в широком динамическом диапазоне и достижения высокой эффективности усилители мощности РЧ (РА) обычно работают в своей нелинейной области. Как показывает эта диаграмма созвездия, нелинейное поведение PA вызывает искажения сигнальных созвездий, которые сжимают амплитуду (искажения AM-AM) и фазу скручивания (искажения AM-PM) точек созвездия, пропорциональную амплитуде точки созвездия.
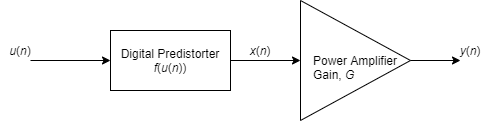
Цель цифрового предыскажения состоит в том, чтобы найти нелинейную функцию, которая линеаризует суммарный эффект нелинейного поведения ПА на выходе ПА в рабочем диапазоне ПА. Когда вход PA равен x (n), а функция предыскажения равна f (u (n)), где u (n) является истинным сигналом, подлежащим усилению, выход PA приблизительно равен G × u (n), где G является желаемым усилением амплитуды PA.
Цифровой предыскажатель может быть сконфигурирован для использования многочлена памяти с перекрестными терминами или без них.
Многочлен памяти с перекрестными терминами предустанавливает входной сигнал как
| u (n-j) | k.
Многочлен памяти с перекрестными членами имеет коэффициенты (M + M × M × (K-1)) для cm и amjk.
Полином памяти без перекрестных терминов предустанавливает входной сигнал как
u (n-m) | k.
Многочлен без перекрестных членов имеет коэффициенты M × K для amk.
Оценка функции предыскажения и коэффициентов
Оценка коэффициента DPD использует непрямую архитектуру обучения, чтобы найти функцию f (u (n)) для прогнозирования входного сигнала u (n), который предшествует входу PA.
Алгоритм оценки коэффициентов DPD моделирует нелинейные эффекты памяти PA, основываясь на работах Morgan и др. [1] и Schetzen [2], используя теоретическую основу, разработанную для систем Volterra.
В частности, обратное отображение из выходного сигнала РА, нормализованного коэффициентом усиления РА, {y (n )/G}, на вход РА, {x (n)}, обеспечивает хорошую аппроксимацию функции f (u (n)), необходимой для предыскажения {u (n)} для получения {x (n)}.
Ссылаясь на вышеприведенные уравнения полинома памяти, вычисляют оценки для коэффициентов «память-полином»:
см и amjk для многочлена памяти с перекрестными терминами
amk для многочлена памяти без перекрестных терминов
Коэффициенты памяти-многочлена оцениваются с использованием алгоритма аппроксимации методом наименьших квадратов или рекурсивного алгоритма аппроксимации методом наименьших квадратов. Алгоритм подгонки наименьших квадратов или алгоритмы рекурсивных наименьших квадратов используют уравнения многочленов памяти выше для многочлена памяти с перекрестными членами или без них путем замены {u (n)} на {y (n )/G}. Порядок функций и размерность матрицы коэффициентов определяются степенью и глубиной многочлена памяти.
Пример, детализирующий процесс точной оценки коэффициентов полинома памяти и предыскажения входного сигнала ПА, см. в разделе Цифровая предистория для компенсации нелинейности усилителя мощности.
Справочный материал см. в работах, перечисленных в [1] и [2].
[1] Морган, Деннис Р., Чжэнсян Ма, Джэхён Ким, Майкл Г. Зиердт и Джон Пасталан. «Обобщенная модель полинома памяти для цифровой предыскажения усилителей мощности». Транзакции IEEE ® при обработке сигналов. Том 54, номер 10, октябрь 2006, стр. 3852-3860.
[2] М. Схецен. Теории нелинейных систем Вольтерры и Винера. Нью-Йорк: Уайли, 1980.
