Exponenta Banner
exponenta event banner

Адаптивные эквалайзеры

Адаптивные структуры эквалайзера обеспечивают неоптимальное выравнивание временных вариаций характеристик канала распространения. Однако эти эквалайзеры привлекательны, поскольку их вычислительная сложность ниже, чем эквалайзеры MLSE.

В Toolbox™ связи, comm.LinearEqualizer и comm.DecisionFeedbackEqualizer Системные объекты и блоки линейного эквалайзера и эквалайзера с решающей обратной связью используют фильтры линии задержки отводов для выравнивания линейно модулированного сигнала через дисперсионный канал. Эти признаки выводят оценку сигнала, используя оценку канала, смоделированного как фильтр с конечным входным откликом (КИХ).

Для декодирования принятого сигнала адаптивный эквалайзер:

  1. Применяет фильтр FIR к символам во входном сигнале. Веса отводов КИХ-фильтра соответствуют оценке канала.

  2. Выводит оценку сигнала и использует оценку сигнала для обновления весов отводов для следующего символа. Оценка сигнала и обновление весов зависят от структуры и алгоритма адаптивного эквалайзера.

Варианты адаптивной структуры эквалайзера представляют собой линейную или обратную связь. Варианты адаптивного алгоритма - это наименьший средний квадрат (LMS), рекурсивный средний квадрат (RMS) или алгоритм постоянного модуля (CMA). Материал фона адаптивных эквалайзеров см. в разделе Выбранные привязки для эквалайзеров.

Количество отводов

Для линейного эквалайзера количество отводов должно быть больше или равно количеству входных выборок на символ. Для эквалайзера обратной связи принятия решения количество прямых отводов должно быть больше или равно количеству входных выборок на символ.

Интервал касания символа

Можно настроить эквалайзер для работы в качестве эквалайзера с интервалом символов или в качестве эквалайзера с интервалом дробных символов.

  • Для работы эквалайзера со скоростью, разнесенной по символам, укажите количество выборок на символ как 1. Эквалайзеры скорости передачи символов имеют отводы, разнесенные по длительности символа. Эквалайзеры скорости передачи символов чувствительны к фазе синхронизации.

  • Для работы эквалайзера с дробной скоростью разнесения символов укажите количество входных выборок на символ как целое число, большее, чем 1 и обеспечивают входной сигнал с избыточной выборкой при этой частоте дискретизации. Дробные эквалайзеры с разнесением символов имеют отводы, разнесенные на целую долю длительности входного символа. Дробные эквалайзеры с разнесением символов не чувствительны к фазе синхронизации.

Примечание

Эквалайзер MLSE поддерживает дробный интервал символов, но использовать его не рекомендуется. Вычислительная сложность и нагрузка MLSE растут экспоненциально с длиной временной дисперсии канала. Избыточная дискретизация входного сигнала означает умножение экспоненциального члена на число выборок на символ.

Линейные эквалайзеры

Линейные эквалайзеры могут удалять межсимвольные помехи (ISI), когда частотная характеристика канала не имеет нуля. Если в частотной характеристике канала имеется нулевое значение, линейные эквалайзеры стремятся усилить шум. В этом случае используйте корректоры обратной связи принятия решения, чтобы избежать усиления шума.

Линейный эквалайзер состоит из отводимой линии задержки, которая хранит выборки из входного сигнала. Один раз за период символа эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса для подготовки к следующему периоду символа.

Линейные эквалайзеры могут быть разнесенными по символам или дробными по символам.

  • Для эквалайзера с разнесением символов число выборок на символ K равно 1. Выходная частота дискретизации равна входной частоте дискретизации.

  • Для эквалайзера с дробными символами число выборок на символ, K, равно целому числу, большему 1. Обычно К равно 4 для дробно разнесенных эквалайзеров. Выходная частота дискретизации равна 1/T, а входная частота дискретизации равна K/T, где T - период символа. Обновление веса отводов происходит с частотой вывода.

На этой схеме показан линейный эквалайзер с L весами, периодом символа Т и К выборок на символ. Если K равно 1, то результатом является линейный эквалайзер с интервалом символов вместо линейного эквалайзера с интервалом дробных символов.

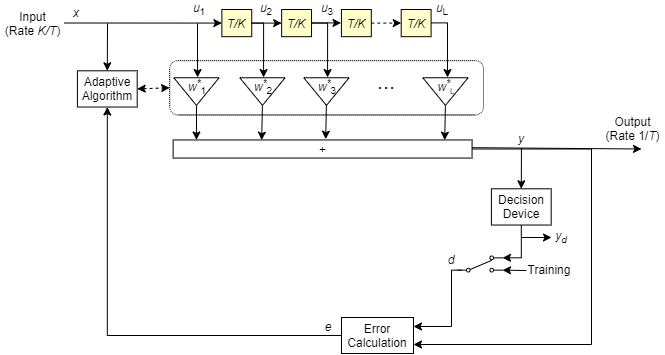
В каждом периоде символа эквалайзер принимает K входных выборок на линии задержки с отводом. Затем эквалайзер выводит взвешенную сумму значений в линии задержки с отводом и обновляет веса для подготовки к следующему периоду символа.

Уравнители обратной связи при принятии решений

Эквалайзер обратной связи принятия решения (DFE) является нелинейным эквалайзером, который уменьшает межсимвольные помехи (ISI) в частотно-селективных каналах. Если в частотной характеристике канала имеется значение null, то DFE не повышают уровень шума. DFE состоит из отводимой линии задержки, которая хранит выборки из входного сигнала и содержит прямой фильтр и фильтр обратной связи. Прямой фильтр подобен линейному эквалайзеру. Фильтр обратной связи содержит отводимую линию задержки, входами которой являются решения, принятые по выровненному сигналу. Один раз за период символа эквалайзер выводит взвешенную сумму значений в линии задержки и обновляет веса для подготовки к следующему периоду символа.

DFE могут быть разнесенными по символам или дробными по символам.

  • Для эквалайзера с разнесением символов число выборок на символ K равно 1. Выходная частота дискретизации равна входной частоте дискретизации.

  • Для эквалайзера с дробными символами число выборок на символ, K, равно целому числу, большему 1. Обычно K равно 4 для дробных эквалайзеров, разнесенных по символам. Выходная частота дискретизации равна 1/T, а входная частота дискретизации равна K/T. Обновление веса отводов происходит с частотой вывода.

На этой схеме показан разделенный на части DFE с общим числом N весов, периодом символа T и K выборок на символ. Фильтр имеет L весов прямой связи и N-L весов обратной связи. Прямой фильтр находится вверху, а фильтр обратной связи - внизу. Если K равно 1, то результатом является DFE с разнесением по символам вместо DFE с разделением по символам.

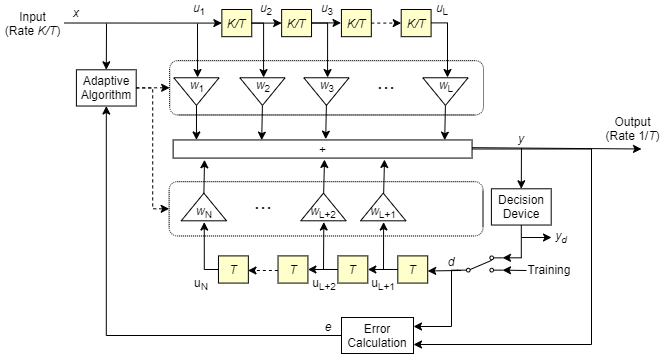
В каждом периоде символа эквалайзер принимает K входных выборок в прямом фильтре и одну решающую или обучающую выборку в фильтре обратной связи. Затем эквалайзер выводит взвешенную сумму значений в прямых линиях задержки и линиях задержки обратной связи и обновляет весовые коэффициенты для подготовки к следующему периоду символа.

Примечание

Алгоритм для блока «Адаптивный алгоритм» в схеме совместно оптимизирует веса прямой и обратной связи. Совместная оптимизация особенно важна для сходимости в алгоритме рекурсивного наименьшего квадрата (RLS).

Опорный сигнал и режимы работы

В приложениях по умолчанию эквалайзер сначала работает в тренировочном режиме для сбора информации о канале. Эквалайзер позже переходит в режим принятия решения.

  • Когда эквалайзер работает в тренировочном режиме, опорный сигнал представляет собой заранее заданную, известную переданную последовательность.

  • Когда эквалайзер работает в режиме принятия решения, опорный сигнал является обнаруженной версией выходного сигнала, обозначенной yd на схеме.

Алгоритм CMA не имеет режима обучения. Режим обучения применяется только в том случае, если эквалайзер настроен на использование алгоритма LMS или RLS.

Расчет ошибок

Операция вычисления ошибок создает сигнал, заданный этим выражением, где R - константа, связанная с сигнальной совокупностью.

e = {d  − y LMS или RLSy (R − | y | 2) CMA

Обновление веса отводов

Для линейных структур и структур эквалайзера с обратной связью, выбор LMS, RLS или CMA определяет алгоритмы, которые используются для установки весов отводов и выполнения вычисления ошибок. Новый набор весов отводов зависит от:

  • Текущий набор весов отводов

  • Входной сигнал

  • Выходной сигнал

  • Опорный сигнал d только для адаптивных алгоритмов LMS и RLS. Характеристики опорного сигнала зависят от режима работы эквалайзера.

Алгоритм наименьшего среднего квадрата

Для алгоритма LMS в предыдущей схеме w является вектором всех весов wi, а u является вектором всех входов ui. На основе текущего набора весов алгоритм LMS создает новый набор весов как

wnew = wcurrent + (StepSize) ue *.

Размер шага, используемый адаптивным алгоритмом, задается как положительный скаляр. Увеличение размера шага уменьшает время сходимости эквалайзера, но приводит к тому, что выровненный выходной сигнал становится менее стабильным. Для определения максимального размера шага, разрешенного при использовании адаптивного алгоритма LMS, используйте maxstep объектная функция. Оператор * обозначает комплексное сопряжение и вычисление ошибки e = d-y.

Рекурсивный алгоритм наименьшего квадрата

Для алгоритма RLS в предыдущей схеме w - вектор всех весов wi, а u - вектор всех входов ui. На основе текущего набора входов u и матрицы обратной корреляции P алгоритм RLS сначала вычисляет вектор коэффициента усиления Калмана K как

K = Pu (ForgingFactor) + uHPu.

Коэффициент забывания, используемый адаптивным алгоритмом, задается как скаляр в диапазоне (0, 1]. Уменьшение коэффициента забывания уменьшает время сходимости эквалайзера, но приводит к тому, что выровненный выходной сигнал становится менее стабильным. H обозначает эрмитово транспонирование. На основе текущей матрицы обратной корреляции новая матрица обратной корреляции

Pnew = (1 − KuH) PcurrentForgedFactor.

На основе текущего набора весов алгоритм RLS создает новый набор весов как

wnew = ток + K * e.

Оператор * обозначает комплексное сопряжение и вычисление ошибки e = d-y.

Алгоритм постоянного модуля

Для адаптивного алгоритма CMA в предыдущей схеме w - вектор всех весов wi, а u - вектор всех входов ui. На основе текущего набора весов адаптивный алгоритм CMA создает новый набор весов как

wnew = wcurrent + (StepSize) u * e.

Размер шага, используемый адаптивным алгоритмом, задается как положительный скаляр. Увеличение размера шага уменьшает время сходимости эквалайзера, но приводит к тому, что выровненный выходной сигнал становится менее стабильным. Для определения максимального размера шага, разрешенного адаптивным алгоритмом CMA, используйте maxstep объектная функция. Оператор * обозначает комплексное сопряжение и вычисление ошибки e = y (R - | y | 2), где R - постоянная, связанная с сигнальной совокупностью.

Настройка адаптивных выравнивателей

Выберите линейную структуру или структуру эквалайзера с обратной связью. Определите, какой адаптивный алгоритм использовать - LMS, RLS или CMA. Укажите настройки для режима работы структуры и алгоритма.

Конфигурирование эквалайзера включает в себя выбор линейной структуры или структуры обратной связи для принятия решения, выбор адаптивного алгоритма и определение конкретных режимов работы структуры и алгоритма.

Решая, какой адаптивный алгоритм наилучшим образом соответствует вашим потребностям, учитывайте:

  • Алгоритм LMS выполняется быстро, но сходится медленно. Его сложность линейно растет с числом весов.

  • Алгоритм RLS быстро сходится. Его сложность растет приблизительно с квадратом числа весов. Этот алгоритм также может быть нестабильным, когда количество весов велико.

  • Алгоритм постоянного модуля (CMA) полезен, когда нет обучающего сигнала. Он лучше всего подходит для постоянных модуляций модуля, таких как PSK.

    • Если CMA не имеет дополнительной побочной информации, это может привести к фазовой неоднозначности. Например, веса, найденные CMA, могут создать совершенную QPSK-совокупность, но ввести поворот фазы на 90, 180 или 270 градусов. В этом случае используют алгоритм коррекции фазовой неоднозначности или выбирают схему дифференциальной модуляции. Схемы дифференциальной модуляции нечувствительны к фазовой неоднозначности.

Для просмотра или изменения любых свойств адаптивного эквалайзера используйте синтаксис, описанный для объектов канала в разделе Отображение и изменение свойств объекта.

Дополнительные сведения о адаптивных алгоритмах см. в разделе Привязки, перечисленные в разделе Выбранные привязки для выравнивателей.

Задание адаптивного эквалайзера

Чтобы создать объект адаптивного эквалайзера для использования в MATLAB ®, выберите comm.LinearEqualizer или comm.DecisionFeedbackEqualizer object™ системы. Для Simulink ® используйте блок «Линейный эквалайзер» или «Корректор с обратной связью принятия решения». На основе характеристик канала распространения в моделировании используйте критерии в Уравнение (Equalization) для выбора структуры эквалайзера.

Объект эквалайзера имеет множество свойств, записывающих информацию о эквалайзере. Свойства могут быть связаны с:

  • Структура эквалайзера, например, количество отводов.

  • Адаптивный алгоритм, используемый эквалайзером, такой как размер шага в алгоритме LMS или CMA.

  • Информация о текущем состоянии эквалайзера. Объект эквалайзера может выводить значения весов.

Для просмотра или изменения любых свойств объекта эквалайзера используйте синтаксис, описанный для объектов канала в разделе Отображение и изменение свойств объекта.

Определение объекта эквалайзера

Открыть сценарий в реальном времени

Код создает объекты эквалайзера для следующих конфигураций:

  • Линейный эквалайзер RLS с 10 весами.

  • Дробно разнесенный линейный корректор RLS с 10 весами, комбинацией BPSK и двумя выборками на символ.

  • Корректор RLS обратной связи принятия решения с тремя весами в фильтре прямой связи и двумя весами в фильтре обратной связи.

Все три объекта эквалайзера задают адаптивный алгоритм RLS с коэффициентом забывания 0,3.

Создайте объекты эквалайзера различных типов. Параметры по умолчанию используются для свойств, не заданных с помощью 'Name,Value' пар.

eqlin = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3)
eqlin = 
  comm.LinearEqualizer with properties:

                          Algorithm: 'RLS'
                            NumTaps: 10
                   ForgettingFactor: 0.3000
    InitialInverseCorrelationMatrix: 0.1000
                      Constellation: [1x4 double]
                       ReferenceTap: 3
                         InputDelay: 0
              InputSamplesPerSymbol: 1
              TrainingFlagInputPort: false
                 AdaptAfterTraining: true
               InitialWeightsSource: 'Auto'
                 WeightUpdatePeriod: 1


eqfrac = comm.LinearEqualizer('Algorithm','RLS','NumTaps',10,'ForgettingFactor',0.3, ...
    'Constellation',[-1 1],'InputSamplesPerSymbol',2)
eqfrac = 
  comm.LinearEqualizer with properties:

                          Algorithm: 'RLS'
                            NumTaps: 10
                   ForgettingFactor: 0.3000
    InitialInverseCorrelationMatrix: 0.1000
                      Constellation: [-1 1]
                       ReferenceTap: 3
                         InputDelay: 0
              InputSamplesPerSymbol: 2
              TrainingFlagInputPort: false
                 AdaptAfterTraining: true
               InitialWeightsSource: 'Auto'
                 WeightUpdatePeriod: 1


eqdfe = comm.DecisionFeedbackEqualizer('Algorithm','RLS','NumForwardTaps',3, ...
    'NumFeedbackTaps',2,'ForgettingFactor',0.3)
eqdfe = 
  comm.DecisionFeedbackEqualizer with properties:

                          Algorithm: 'RLS'
                     NumForwardTaps: 3
                    NumFeedbackTaps: 2
                   ForgettingFactor: 0.3000
    InitialInverseCorrelationMatrix: 0.1000
                      Constellation: [1x4 double]
                       ReferenceTap: 3
                         InputDelay: 0
              InputSamplesPerSymbol: 1
              TrainingFlagInputPort: false
                 AdaptAfterTraining: true
               InitialWeightsSource: 'Auto'
                 WeightUpdatePeriod: 1

Назначение адаптивного алгоритма

Открыть сценарий в реальном времени

Используйте Algorithm для назначения адаптивного алгоритма, используемого эквалайзером.

Назначение алгоритма

При создании объекта эквалайзера назначьте адаптивный алгоритм.

eqlms = comm.LinearEqualizer('Algorithm','LMS');

Создайте объект эквалайзера с настройками свойств по умолчанию. LMS является адаптивным алгоритмом по умолчанию.

eqrls = comm.LinearEqualizer;
eqrls.Algorithm
ans = 
'LMS'

Обновление eqrls для использования адаптивного алгоритма RLS. 

eqrls.Algorithm = 'RLS';
eqrls.Algorithm
ans = 
'RLS'

Клонирование и дублирование объектов

Настройте новый объект эквалайзера путем клонирования существующего объекта эквалайзера и последующего изменения его свойств. Клон eqlms для создания независимого эквалайзера, eqcma, затем обновите алгоритм до 'CMA'.

eqcma = clone(eqlms);
eqcma.Algorithm
ans = 
'LMS'

eqcma.Algorithm = 'CMA';
eqcma.Algorithm
ans = 
'CMA'

Если требуется независимый дубликат, используйте clone команда.

eqlms.NumTaps
ans = 5

eq2 = eqlms;
eq2.NumTaps = 6;
eq2.NumTaps
ans = 6

eqlms.NumTaps
ans = 6

clone создает копию eqlms который не зависит от eqlms. Напротив, команда eqB = eqA создает eqB как ссылка на eqA, так что eqB и eqA всегда имеют одинаковые параметры свойств.

Обучение эквалайзеру

Линейное выравнивание системы с использованием различных схем обучения

Открыть сценарий в реальном времени

Продемонстрировать линейное выравнивание с использованием алгоритма наименьших средних квадратов (LMS) для восстановления символов QPSK, прошедших через канал AWGN. Примените различные схемы обучения эквалайзера и покажите величину ошибки символа.

Настройка системы

Моделирование QPSK-модулированной системы, подверженной AWGN. Передача пакетов, состоящих из 200 обучающих символов и 1800 случайных символов данных. Сконфигурируйте линейный эквалайзер LMS для восстановления пакетных данных.

M = 4;
numTrainSymbols = 200;
numDataSymbols = 1800;
SNR = 20;
trainingSymbols = pskmod(randi([0 M-1],numTrainSymbols,1),M,pi/4);
numPkts = 10;
lineq = comm.LinearEqualizer('Algorithm','LMS', ...
    'NumTaps',5,'ReferenceTap',3,'StepSize',0.01);

Обучение эквалайзера в начале каждого пакета с сбросом

Используйте символы предварительного обучения при обработке каждого пакета. После обработки каждого пакета выполните сброс эквалайзера. Этот сброс заставляет эквалайзер обучать отводы без предварительного знания. Графики сигнала ошибки эквалайзера для первого, второго и последнего пакета показывают более высокие ошибки символов в начале каждого пакета.

jj = 1;
figure
for ii = 1:numPkts
    b = randi([0 M-1],numDataSymbols,1);
    dataSym = pskmod(b,M,pi/4);
    packet = [trainingSymbols;dataSym];
    rx = awgn(packet,SNR);
    [~,err] = lineq(rx,trainingSymbols);
    reset(lineq)
    if (ii ==1 || ii == 2 ||ii == numPkts)
        subplot(3,1,jj)
        plot(abs(err))
        title(['Packet # ',num2str(ii)])
        xlabel('Symbols')
        ylabel('Error Magnitude')
        axis([0,length(packet),0,1])
        grid on;
        jj = jj+1;
    end
end

Figure contains 3 axes. Axes 1 with title Packet # 1 contains an object of type line. Axes 2 with title Packet # 2 contains an object of type line. Axes 3 with title Packet # 10 contains an object of type line.

Обучение эквалайзера в начале каждого пакета без сброса

Обработка каждого пакета с использованием добавочных обучающих символов. Не сбрасывайте эквалайзер после обработки каждого пакета. Не сбрасывая после каждого пакета, эквалайзер сохраняет веса отводов от предыдущих пакетов. Графики сигнала ошибки эквалайзера для первого, второго и последнего пакета показывают, что после начальной тренировки по первому пакету последующие пакеты имеют меньшее количество символьных ошибок в начале каждого пакета.

release(lineq)
jj = 1;
figure
for ii = 1:numPkts
    b = randi([0 M-1],numDataSymbols,1);
    dataSym = pskmod(b,M,pi/4);
    packet = [trainingSymbols;dataSym];
    channel = 1;
    rx = awgn(packet*channel,SNR);
    [~,err] = lineq(rx,trainingSymbols);
    if (ii ==1 || ii == 2 ||ii == numPkts)
        subplot(3,1,jj)
        plot(abs(err))
        title(['Packet # ',num2str(ii)])
        xlabel('Symbols')
        ylabel('Error Magnitude')
        axis([0,length(packet),0,1])
        grid on;
        jj = jj+1;
    end
end

Figure contains 3 axes. Axes 1 with title Packet # 1 contains an object of type line. Axes 2 with title Packet # 2 contains an object of type line. Axes 3 with title Packet # 10 contains an object of type line.

Периодическое обучение эквалайзера

Системы с сигналами, подлежащими изменению во времени каналов, требуют периодической тренировки эквалайзера для поддержания фиксации изменений канала. Укажите систему, которая имеет 200 символов обучения для каждых 1800 символов данных. Между тренировками эквалайзер не обновляет веса отводов. Эквалайзер обрабатывает 200 символов на пакет.

Rs = 1e6;
fd = 20;
spp = 200; % Symbols per packet
b = randi([0 M-1],numDataSymbols,1);
dataSym = pskmod(b,M,pi/4);
packet = [trainingSymbols; dataSym];
stream = repmat(packet,10,1);
tx = (0:length(stream)-1)'/Rs;
channel = exp(1i*2*pi*fd*tx);
rx = awgn(stream.*channel,SNR);

Установите AdaptAfterTraining свойство для false для остановки обновления веса отводов эквалайзера после фазы обучения.

release(lineq)
lineq.AdaptAfterTraining = false
lineq = 
  comm.LinearEqualizer with properties:

                Algorithm: 'LMS'
                  NumTaps: 5
                 StepSize: 0.0100
            Constellation: [1x4 double]
             ReferenceTap: 3
               InputDelay: 0
    InputSamplesPerSymbol: 1
    TrainingFlagInputPort: false
       AdaptAfterTraining: false
     InitialWeightsSource: 'Auto'
       WeightUpdatePeriod: 1

Выровнять поврежденные данные. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и совокупности сигналов. При изменении канала выходной сигнал эквалайзера не удаляет эффекты канала. Выходная совокупность вращается несинхронизированно, что приводит к битовым ошибкам. 

[y,err] = lineq(rx,trainingSymbols);

figure
subplot(2,1,1)
plot(tx, unwrap(angle(channel)))
xlabel('Time (sec)')
ylabel('Channel Angle (rad)')
title('Angular Error Over Time')
subplot(2,1,2)
plot(abs(err))
xlabel('Symbols')
ylabel('Error Magnitude')
grid on
title('Time-Varying Channel Without Retraining')

Figure contains 2 axes. Axes 1 with title Angular Error Over Time contains an object of type line. Axes 2 with title Time-Varying Channel Without Retraining contains an object of type line.

scatterplot(y)

Figure Scatter Plot contains an axes. The axes with title Scatter plot contains an object of type line. This object represents Channel 1.

Установите TrainingInputPort свойство для true конфигурирование эквалайзера для переподготовки отводов при сигнале trainFlag вход. Эквалайзер работает только тогда, когда trainFlag является true. После каждых 2000 символов эквалайзер перестраивает отводы и фиксирует изменения канала. Постройте график угловой ошибки из канала, сигнала ошибки эквалайзера и совокупности сигналов. При изменении канала выходной сигнал эквалайзера удаляет эффекты канала. Выходная совокупность не вращается вне синхронизации и битовые ошибки уменьшаются.

release(lineq)
lineq.TrainingFlagInputPort = true;
symbolCnt = 0;
numPackets = length(rx)/spp;
trainFlag = true;
trainingPeriod = 2000;
eVec = zeros(size(rx));
yVec = zeros(size(rx));
for p=1:numPackets
    [yVec((p-1)*spp+1:p*spp,1),eVec((p-1)*spp+1:p*spp,1)] = ...
        lineq(rx((p-1)*spp+1:p*spp,1),trainingSymbols,trainFlag);
    symbolCnt = symbolCnt + spp;
    if symbolCnt >= trainingPeriod
        trainFlag = true;
        symbolCnt = 0;
    else
        trainFlag = false;
    end
end
figure
subplot(2,1,1)
plot(tx, unwrap(angle(channel)))
xlabel('t (sec)')
ylabel('Channel Angle (rad)')
title('Angular Error Over Time')
subplot(2,1,2)
plot(abs(eVec))
xlabel('Symbols')
ylabel('Error Magnitude')
grid on
title('Time-Varying Channel With Retraining')

Figure contains 2 axes. Axes 1 with title Angular Error Over Time contains an object of type line. Axes 2 with title Time-Varying Channel With Retraining contains an object of type line.

scatterplot(yVec)

Figure Scatter Plot contains an axes. The axes with title Scatter plot contains an object of type line. This object represents Channel 1.

Линейное выравнивание символов с помощью обучения на основе EVM

Открыть сценарий в реальном времени

Восстановление символов QPSK с помощью линейного эквалайзера с использованием алгоритма постоянного модуля (CMA) и обучения отводам на основе EVM. При использовании алгоритмов слепого эквалайзера, таких как CMA, обучайте отводы эквалайзера с помощью AdaptWeights свойство для запуска и остановки обучения. Вспомогательные функции используются для создания графиков и применения фазовой коррекции.

Инициализация системных переменных.

rng(123456);
M = 4; % QPSK
numSymbols = 100;
numPackets = 5000;
raylChan = comm.RayleighChannel('PathDelays',[0 1], ...
    'AveragePathGains',[0 -12],'MaximumDopplerShift',1e-5);
SNR = 50;
adaptWeights = true;

Создайте объекты эквалайзера и системы EVM. Объект equalizer System определяет линейный эквалайзер с помощью адаптивного алгоритма CMA. Вызовите вспомогательную функцию для инициализации рисунков.

lineq = comm.LinearEqualizer('Algorithm','CMA', ...
    'NumTaps',5,'ReferenceTap',3, ...
    'StepSize',0.03,'AdaptWeightsSource','Input port')
lineq = 
  comm.LinearEqualizer with properties:

                Algorithm: 'CMA'
                  NumTaps: 5
                 StepSize: 0.0300
            Constellation: [1x4 double]
             ReferenceTap: 3
    InputSamplesPerSymbol: 1
       AdaptWeightsSource: 'Input port'
     InitialWeightsSource: 'Auto'
       WeightUpdatePeriod: 1


info(lineq)
ans = struct with fields:
    Latency: 2


evm = comm.EVM('ReferenceSignalSource', ...
    'Estimated from reference constellation');
[errPlot,evmPlot,scatSym,adaptState] = initFigures(numPackets,lineq);

Контур выравнивания

Для реализации цикла выравнивания:

  1. Создание пакетов данных PSK.

  2. Примените к данным передачи релеевское замирание и AWGN.

  3. Примените выравнивание к принятым данным и фазовую коррекцию к выходу эквалайзера.

  4. Оцените EVM и переключите переключатель adaptWeights флаг для true или false на основе уровня EVM.

  5. Обновите рисунки.

for p=1:numPackets
    data = randi([0 M-1],numSymbols,1);
    tx = pskmod(data,M,pi/4);
    rx = awgn(raylChan(tx),SNR);
    rxDelay = finddelay(rx,tx);
    [y,err,wts] = lineq(rx,adaptWeights);
    y = phaseCorrection(y);
    evmEst = evm(y);
    adaptWeights = (evmEst > 20);
    
    updateFigures(errPlot,evmPlot,scatSym,adaptState, ...
        wts,y(end),evmEst,adaptWeights,p,numPackets)
end

Figure contains 4 axes. Axes 1 with title Tap Weight Magnitude contains an object of type stem. Axes 2 with title Scatter Plot contains an object of type line. Axes 3 with title Adapt Weights Signal contains an object of type line. Axes 4 with title EVM contains an object of type line.

rxDelay
rxDelay = 0

Графики показывают, что по мере изменения EVM эквалайзер переключается в режим адаптации веса, направленный на принятие решения, и выходит из него.

Вспомогательные функции

Эта вспомогательная функция инициализирует фигуры, показывающие четверной график результатов моделирования.

function [errPlot,evmPlot,scatter,adaptState] = initFigures(numPkts,lineq)
yVec = nan(numPkts,1);
evmVec = nan(numPkts,1);
wVec = zeros(lineq.NumTaps,1);
adaptVec = nan(numPkts,1);

figure
subplot(2,2,1)
evmPlot = stem(wVec);
grid on; axis([1 lineq.NumTaps 0 1.8])
xlabel('Taps'); ylabel('|Weights|'); title('Tap Weight Magnitude')

subplot(2,2,2)
scatter = plot(yVec, '.');
axis square; axis([-1.2 1.2 -1.2 1.2]); grid on
xlabel('In-phase'); ylabel('Quadrature'); title('Scatter Plot');
subplot(2,2,3)
adaptState = plot(adaptVec);
grid on; axis([0 numPkts -0.2 1.2])
ylabel('Training'); xlabel('Symbols'); title('Adapt Weights Signal')
subplot(2,2,4)
errPlot = plot(evmVec);
grid on; axis([1 numPkts 0 100])
xlabel('Symbols'); ylabel('EVM (%)'); title('EVM')
end

Эта вспомогательная функция обновляет цифры.

function updateFigures(errPlot,evmPlot,scatSym, ...
    adaptState,w,y,evmEst,adaptWts,p,numFrames)
persistent yVec evmVec adaptVec

if p == 1
    yVec = nan(numFrames,1);
    evmVec = nan(numFrames,1);
    adaptVec = nan(numFrames,1);
end

yVec(p) = y;
evmVec(p) = evmEst;
adaptVec(p) = adaptWts;

errPlot.YData = abs(evmVec);
evmPlot.YData = abs(w);
scatSym.XData = real(yVec);
scatSym.YData = imag(yVec);
adaptState.YData = adaptVec;
drawnow limitrate
end

Эта вспомогательная функция применяет фазовую коррекцию.

function y = phaseCorrection(y)
a = angle(y((real(y) > 0) & (imag(y) > 0)));
a(a < 0.1) = a(a < 0.1) + pi/2;
theta = mean(a) - pi/4;
y = y * exp(-1i*theta);
end

Управление задержками при использовании выравнивателей

Для правильного выравнивания необходимо определить и учесть системные задержки. Как показано в следующем примере, можно использовать finddelay для определения системной задержки. В этом примере используется линейное выравнивание LMS, но тот же подход применим для адаптивных алгоритмов RLS и CMA и для эквалайзеров обратной связи принятия решений.

Линейно выравнивать задержанный сигнал

Открыть сценарий в реальном времени

Моделирование системы с задержкой между переданными символами и принятыми выборками. Типичные системы имеют фильтры передатчика и приемника, которые приводят к задержке. Эта задержка должна быть учтена для синхронизации системы. В этом примере системная задержка вводится без фильтров передачи и приема. Линейное выравнивание, используя алгоритм наименьших средних квадратов (LMS), восстанавливает символы QPSK.

Инициализация переменных моделирования.

M = 4; % QPSK
numSymbols = 10000;
numTrainingSymbols = 1000;
mpChan = [1 0.5*exp(1i*pi/6) 0.1*exp(-1i*pi/8)];
systemDelay = dsp.Delay(20);
snr = 24;

Формирование QPSK-модулированных символов. Применение фильтрации каналов многолучевого распространения, системной задержки и AWGN к передаваемым символам.

data = randi([0 M-1],numSymbols,1);
tx = pskmod(data,M,pi/4); % OQPSK
delayedSym = systemDelay(filter(mpChan,1,tx));
rx = awgn(delayedSym,snr,'measured');

Создайте объекты эквалайзера и системы EVM. Объект equalizer System определяет линейный эквалайзер, использующий алгоритм LMS.

lineq = comm.LinearEqualizer('Algorithm','LMS', ...
    'NumTaps',9,'ReferenceTap',5);
evm = comm.EVM('ReferenceSignalSource', ...
    'Estimated from reference constellation');

Уравнять без регулировки задержки на входе

Выравнивание полученных символов.

[y1,err1,wts1] = lineq(rx,tx(1:numTrainingSymbols,1));

Найдите задержку между принятыми символами и переданными символами с помощью finddelay функция.

rxDelay = finddelay(tx,rx)
rxDelay = 20

Просмотрите информацию эквалайзера. Значение задержки указывает задержку, введенную корректором. Вычислить общую задержку как сумму rxDelay и задержка эквалайзера.

eqInfo = info(lineq)
eqInfo = struct with fields:
    Latency: 4


totalDelay = rxDelay + eqInfo.Latency;

Пока выходной сигнал эквалайзера не сойдется, частота ошибок символов высока. Постройте график вывода ошибки, err1, чтобы определить, когда выравниваемый выходной сигнал сходится. 

plot(abs(err1))
xlabel('Symbols')
ylabel('Error Magnitude')
title('Equalizer Error Signal')

Figure contains an axes. The axes with title Equalizer Error Signal contains an object of type line.

График показывает чрезмерные ошибки за пределами периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, чтобы учесть несвергнутый выходной сигнал и системную задержку между выходным сигналом эквалайзера и переданными символами, пропускают первые 2000 символов. 

dataRec1 = pskdemod(y1(2000+totalDelay:end),M,pi/4);
symErrWithDelay = symerr(data(2000:end-totalDelay),dataRec1)
symErrWithDelay = 5999

evmWithDelay = evm(y1)
evmWithDelay = 29.5795

Частота ошибок и EVM высоки, поскольку задержка приема не была учтена в системном объекте эквалайзера.

Настройка задержки на входе в эквалайзере

Выравнивание полученных данных с помощью значения задержки для установки InputDelay собственность. Поскольку InputDelay является неперестраиваемым свойством, необходимо освободить lineq Системный объект для изменения конфигурации InputDelay собственность. Выравнивание полученных символов.

release(lineq)
lineq.InputDelay = rxDelay
lineq = 
  comm.LinearEqualizer with properties:

                Algorithm: 'LMS'
                  NumTaps: 9
                 StepSize: 0.0100
            Constellation: [1x4 double]
             ReferenceTap: 5
               InputDelay: 20
    InputSamplesPerSymbol: 1
    TrainingFlagInputPort: false
       AdaptAfterTraining: true
     InitialWeightsSource: 'Auto'
       WeightUpdatePeriod: 1


[y2,err2,wts2] = lineq(rx,tx(1:numTrainingSymbols,1));

Постройте график весов отводов и выровненной величины ошибки. Блок-график показывает веса отводов эквалайзера до и после удаления системной задержки. График линии 2-D показывает более медленную конвергенцию эквалайзера для задержанного сигнала по сравнению с сигналом с удаленной задержкой.

subplot(2,1,1)
stem([real(wts1),real(wts2)])
xlabel('Taps')
ylabel('Tap Weight Real')
legend('rxDelayed','rxDelayRemoved')
grid on
subplot(2,1,2)
stem([imag(wts1),imag(wts2)])
xlabel('Taps')
ylabel('Tap Weight Imaginary')
legend('rxDelayed','rxDelayRemoved')
grid on

Figure contains 2 axes. Axes 1 contains 2 objects of type stem. These objects represent rxDelayed, rxDelayRemoved. Axes 2 contains 2 objects of type stem. These objects represent rxDelayed, rxDelayRemoved.

figure
plot([abs(err1),abs(err2)])
xlabel('Symbols')
ylabel('Error Magnitude')
legend('rxDelayed','rxDelayRemoved')
grid on

Figure contains an axes. The axes contains 2 objects of type line. These objects represent rxDelayed, rxDelayRemoved.

Вывод ошибки графика уравниваемых сигналов, rxDelayed и rxDelayRemoved. Для сигнала, для которого удалена задержка, эквалайзер сходится в течение периода обучения 1000 символов. При демодуляции символов и вычислении ошибок символов, чтобы учесть несвергнутый выходной сигнал и системную задержку между выходным сигналом эквалайзера и переданными символами, пропускают первые 500 символов. Реконфигурирование эквалайзера для учета системной задержки обеспечивает лучшее выравнивание сигнала и уменьшает ошибки символов и EVM.

eqInfo = info(lineq)
eqInfo = struct with fields:
    Latency: 4


totalDelay = rxDelay + eqInfo.Latency;
dataRec2 = pskdemod(y2(500+totalDelay:end),M,pi/4);
symErrDelayRemoved = symerr(data(500:end-totalDelay),dataRec2)
symErrDelayRemoved = 0

evmDelayRemoved = evm(y2(500+totalDelay:end))
evmDelayRemoved = 9.4435

Использование адаптивных выравнивателей в Simulink

Адаптивное выравнивание с фильтрацией и каналом замирания

В этом примере используются:

Открыть модель

Эта модель показывает поведение выбранного адаптивного эквалайзера в линии связи, имеющей канал замирания. Передатчик и приемник имеют корневую фильтрацию в форме приподнятого косинусного импульса. Блок подсистемы позволяет выбирать между линейными или решающими эквалайзерами обратной связи, использующими адаптивный алгоритм наименьшего квадрата (LMS) или рекурсивного наименьшего квадрата (RLS).

Структура модели

  • Передатчик генерирует данные 16QAM случайных сигналах, которые включают в себя обучающую последовательность и применяет фильтрацию в форме корневого приподнятого косинусного импульса.

  • Ухудшение канала включает в себя замирание многолучевого распространения, доплеровский сдвиг, смещение несущей частоты, переменную целочисленную задержку, потерю пути свободного пространства и AWGN.

  • Приемник применяет фильтрацию в форме корневого приподнятого косинусного импульса, регулирует коэффициент усиления, включает управление режимом эквалайзера для разрешения тренировки и позволяет выбрать алгоритм эквалайзера из этих вариантов.

$$ \begin{array}{|l|l|c|} \hline\vphantom{\displaystyle\int}&#xA;\mathbf{Selection}&#38;\begin{array}{l}\mathbf{Equalizer\&#xA;Algorithm}\end{array}\\ \hline\mathrm{LMS\&#xA;Linear}&#38;\begin{array}{l}\mathrm{Linear\ least\ mean\ square\&#xA;equalizer}\end{array}\\ \hline\mathrm{LMS\&#xA;DFE}&#38;\begin{array}{l}\mathrm{Decision\ feedback\ least\ mean\ square\&#xA;equalizer}\end{array}\\ \hline\mathrm{RLS\&#xA;Linear}&#38;\begin{array}{l}\mathrm{Linear\ recursive\ least\ square\&#xA;equalizer}\end{array}\\ \hline\mathrm{RLS\&#xA;DFE}&#38;\begin{array}{l}\mathrm{Decision\ feedback\ recursive\ least\&#xA;square\ equalizer}\end{array}\\ \hline\end{array} $$

  • Области действия помогают понять, как ведут себя различные эквалайзеры и адаптивные алгоритмы.

Изучение примера модели

Экспериментирование с моделью

Эта модель предоставляет несколько способов изменения настроек и наблюдения за результатами. InitFcn найдено в File>Model Properties>Callbacks требования cm_ex_adaptive_eq_with_fading_init для инициализации модели. Этот файл позволяет изменять настройки модели, в том числе:

  • Системные параметры, такие как SNR.

  • Параметры фильтра формирования импульсов, такие как откат и длина фильтра

  • Значение потери пути.

  • Условия канала: релеевское или рисийское замирание, усиление канала, задержки канала и доплеровский сдвиг.

  • Выбор и конфигурация эквалайзера.

Рекомендации по модели

Этот нестандартный канал связи является репрезентативным для современной системы связи.

  • Оптимальная конфигурация эквалайзера зависит от условий канала. Файл инициализации устанавливает параметры канала доплеровского сдвига и многолучевого замирания, которые выделяют возможности различных эквалайзеров.

  • Структура эквалайзера с обратной связью принятия решения работает лучше, чем структура линейного эквалайзера для более высоких межсимвольных помех.

  • Алгоритм RLS работает лучше, чем алгоритм LMS для более высоких доплеровских частот.

  • Алгоритм LMS выполняется быстро, сходится медленно, и его сложность линейно растет с числом весов.

  • Алгоритм RLS быстро сходится, его сложность растет примерно как квадрат числа весов. Она может быть нестабильной, когда количество весов велико.

  • Каналы, используемые для различных эквалайзеров, имеют следующие характеристики.

$$ \begin{array}{|l|l|c|} \hline\vphantom{\displaystyle\int}&#xA;\mathbf{Selection}&#38;\begin{array}{l}\mathbf{Channel\&#xA;Characteristics}\end{array}\\ \hline\mathrm{LMS\&#xA;Linear}&#38;\begin{array}{l}\mathrm{3\ tap\ multipath\ fading\ channel\ with\&#xA;10\ Hz\ Doppler\ shift}\end{array}\\ \hline\mathrm{LMS\&#xA;DFE}&#38;\begin{array}{l}\mathrm{5\ tap\ multipath\ fading\ channel\ with\&#xA;25\ Hz\ Doppler\ shift}\end{array}\\ \hline\mathrm{RLS\&#xA;Linear}&#38;\begin{array}{l}\mathrm{2\ tap\ multipath\ fading\ channel\ with\&#xA;70\ Hz\ Doppler\ shift}\end{array}\\ \hline\mathrm{RLS\&#xA;DFE}&#38;\begin{array}{l}\mathrm{5\ tap\ multipath\ fading\ channel\ with\&#xA;100\ Hz\ Doppler\ shift}\end{array}\\ \hline\end{array} $$

  • Начальные настройки для других нарушений канала одинаковы для всех эквалайзеров. Значение смещения несущей частоты устанавливают равным 50 Гц. Потеря пути свободного пространства установлена в 60 дБ. Переменная целочисленная задержка устанавливается равной 2 выборкам, что требует от эквалайзеров выполнения некоторого восстановления синхронизации.

Глубокие затухания каналов и потери в тракте могут привести к тому, что уровень входного сигнала эквалайзера будет намного меньше желаемого уровня выходного сигнала, что приведет к неприемлемо длинному времени сходимости эквалайзера. AGC блок регулирует величину принятого сигнала для уменьшения времени сходимости эквалайзера. Необходимо настроить оптимальный уровень выходной мощности усиления на основе выбранной схемы модуляции. Для 16QAM используется требуемая выходная мощность 10 Вт.

Обучение эквалайзера производится в начале моделирования.

Выполнение моделирования

При выполнении моделирования вычисляется статистика ошибок символов и получаются следующие цифры:

  • Диаграмма созвездия сигнала после фильтра приема.

  • Диаграмма созвездия сигнала после регулировки коэффициента усиления.

  • Диаграмма созвездия сигнала после выравнивания с показанными измерениями качества сигнала.

  • График ошибок эквалайзера.

Для графиков, показанных здесь, выбран алгоритм эквалайзера RLS Linear. Отслеживая эти цифры, можно увидеть, что качество принимаемого сигнала колеблется по мере выполнения моделирования.

Графики After Rx Filter и After AGC constellation показывают сигнал перед выравниванием. После АРУ показывает влияние условий канала на передаваемый сигнал. График After Eq показывает сигнал после выравнивания. Сигнал, нанесенный на график созвездия после выравнивания, показывает изменение качества сигнала на основе эффективности процесса выравнивания. На протяжении всего моделирования сигнальные совокупности, построенные перед выравниванием, заметно отклоняются от 16QAM сигнальной совокупности. Созвездие After Eq улучшается или ухудшается по мере изменения сигнала ошибки эквалайзера. Eq error отображается на графике Eq Error, указывает на плохое выравнивание в начале моделирования. Ошибка сначала ухудшается, а затем улучшается, когда выравниватель сходится.

Дальнейшие исследования

Дважды щелкните значок Equalizer Selector и выберите другой эквалайзер. Выполните моделирование для просмотра производительности различных опций эквалайзера. Для сравнения результатов этого эксперимента можно использовать регистратор сигналов. На блок-схеме щелкните правой кнопкой мыши сигнальные провода и выберите Log Selected Signals. Если регистрация сигналов включена, после завершения моделирования откройте инспектор данных моделирования для просмотра зарегистрированных сигналов.

В командной строке MATLAB™ введите edit cm_ex_adaptive_eq_with_fading_init.m чтобы открыть файл инициализации, измените параметр и снова запустите моделирование. Например, настройте характеристики канала (params.maxДоплер | ,params.pathDelays, и params.pathGains). Адаптивный алгоритм RLS работает лучше, чем адаптивный алгоритм LMS, по мере увеличения максимального доплеровского значения.

См. также

Объекты

Блоки

Связанные темы

Документация по инструментам связи

Поддержка