Используя Communications Toolbox™ можно реализовать затухающие каналы с помощью объектов или блоков. Релеевские и рисийские каналы замирания являются полезными моделями реальных явлений в беспроводной связи. Эти явления включают в себя эффекты многолучевого рассеяния, временную дисперсию и доплеровские сдвиги, которые возникают в результате относительного движения между передатчиком и приемником. В этом разделе приводится краткий обзор замирающих каналов и описывается, как их реализовать с помощью инструментария.
На этой фигуре изображены прямые и основные отраженные пути между стационарным радиопередатчиком и подвижным приемником. Затененные формы представляют отражатели, такие как здания.
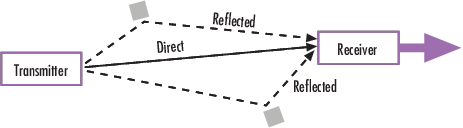
Основные тракты приводят к приходу отложенных версий сигнала в приемник. Кроме того, радиосигнал подвергается рассеянию в локальном масштабе для каждого основного тракта. Такое локальное рассеяние обычно является результатом отражений от объектов вблизи мобильного устройства. Эти неразрешимые компоненты объединяются в приемнике и вызывают явление, известное как многолучевое замирание. Из-за этого явления каждый главный тракт ведет себя как дискретный тракт замирания. Как правило, процесс замирания характеризуется распределением Рэлея для пути без линии визирования и распределением Рисика для пути линии визирования.
Относительное движение между передатчиком и приемником вызывает доплеровские сдвиги. Локальное рассеяние обычно происходит под многими углами вокруг мобильного устройства. Этот сценарий вызывает диапазон доплеровских сдвигов, известный как доплеровский спектр. Максимальный доплеровский сдвиг соответствует локальным компонентам рассеяния, направление которых точно противоположно траектории движения подвижного устройства.
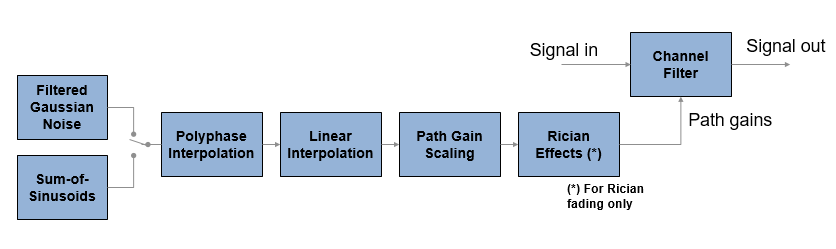
Канальный фильтр применяет коэффициенты усиления тракта к входному сигналу, Signal in. Усиление пути конфигурируется на основе настроек, выбранных в объекте или блоке канала замирания.
Эти блоки и объекты позволяют моделировать каналы замирания SISO или MIMO.
| Инструмент | SISO | MIMO |
|---|---|---|
| MATLAB ® | ||
| Симулинк ® |
Модель канала основной полосы частот для сценариев многолучевого распространения, реализуемая с использованием объектов, включает в себя:
N дискретных путей замирания. Каждый тракт имеет собственную задержку и среднее усиление мощности. Канал, для которого N = 1, называется частотно-плоским каналом замирания. Канал, для которого N > 1 воспринимается как частотно-избирательный канал замирания сигналом достаточно широкой полосы частот.
Модель Рэлея или Rician для каждого пути.
Моделирование пути канала по умолчанию с использованием доплеровского спектра Джейкса с максимальным доплеровским сдвигом, который может быть задан. К другим видам доплеровских спектров, разрешенным (идентичным или различным для всех путей), относятся: плоский, ограниченный Джейкс, асимметричный Джейкс, гауссов, би-гауссов, округлый и колокол.
Если максимальный доплеровский сдвиг установлен в 0 или опущен во время построения объекта канала, то объект моделирует канал как статический. Для этой конфигурации замирание не развивается со временем, и указанный доплеровский спектр не влияет на процесс замирания.
Дополнительная информация о типичных значениях задержек и выигрышей приведена в разделе Выбор реалистичных значений свойств канала.
Библиотека блоков каналов включает в себя блоки замирания MIMO и SISO, которые могут имитировать реальные явления в мобильной связи. Эти явления включают в себя эффекты многолучевого рассеяния в дополнение к доплеровским сдвигам, возникающим из-за относительного движения между передатчиком и приемником.
Совет
Для моделирования канала, который включает как замирание, так и аддитивный белый гауссов шум, используйте блок канала замирания, за которым следует блок канала AWGN.
Блоки MIMO Fading Channel и SISO Fading Channel могут быть установлены для модели распределений Rayleigh или Rician fading канала. В зависимости от типа тракта сигнала выберите распределение замирания для использования.
| Сигнальный тракт | Распределение замирания |
|---|---|
| Прямая линия визирования от передатчика к приемнику | Rician |
| Один или несколько основных отраженных трактов от передатчика к приемнику | Rayleigh |
Можно использовать один экземпляр блока канала замирания, сконфигурированного для распределения релеевского замирания, для моделирования нескольких основных отраженных путей одновременно.
Важно выбрать соответствующие параметры блока для вашей ситуации. Дополнительные сведения см. в разделах «Выбор реалистичных значений свойств канала» и «Ссылки на блоки канала замирания MIMO и канала замирания SISO».
Характеристики канала замирания можно просмотреть с помощью инструментов визуализации канала. Дополнительные сведения см. в разделе Визуализация каналов.
Система связи, включающая канал замирания, обычно требует компонентов, которые компенсируют реакцию замирания. Типичные подходы к компенсации замирания включают в себя:
Дифференциальная модуляция или одноконтурный эквалайзер помогает компенсировать частотно-плоский канал замирания. Для получения информации о реализации дифференциальной модуляции см. справочную страницу блока основной полосы частот модулятора M-DPSK.
Эквалайзер с множеством отводов помогает компенсировать частотно-избирательный канал замирания. Дополнительные сведения см. в разделе Уравнение.
Пример линии связи с адаптивным выравниванием иллюстрирует, почему необходимо компенсировать замирание канала.
Имитаторы каналов многолучевого распространения Rayleigh и Rician в Communications Toolbox используют ограниченную полосой дискретную модель канала многолучевого распространения раздела 9.1.3.5.2 в [1]. Эта реализация предполагает, что профиль мощности задержки и доплеровский спектр канала являются разделяемыми [1]. Поэтому многолучевой канал замирания моделируется как линейный фильтр с конечной импульсной характеристикой (КИХ). Пусть обозначает набор выборок на входе в канал. Затем отсчеты на выходе канала связаны с через:
где - набор весов отводов, задаваемый следующим образом:
В уравнениях:
- период входной выборки для канала.
, где - набор задержек пути. K - общее количество трактов в канале многолучевого замирания.
, где набор комплексных коэффициентов усиления тракта канала многолучевого замирания. Эти усиления пути не коррелируются друг с другом.
и выбраны так, чтобы | был мал, когда n меньше N1 или N2.
Два метода, отфильтрованный гауссов шум и сумма синусоид, используются для генерации набора комплексных коэффициентов усиления тракта, .
Каждый процесс усиления тракта генерируется следующими шагами:
Метод отфильтрованного гауссова шума
Сложный некоррелированный (белый) гауссов процесс с нулевой средней и единичной дисперсией генерируется за дискретное время.
Комплексный гауссов процесс фильтруется доплеровским фильтром с частотным откликом (f), S (f) обозначает желаемый спектр доплеровской мощности.
Отфильтрованный комплексный процесс Гаусса интерполируется таким образом, что его период выборки согласуется с периодом выборки входного сигнала. Используется комбинация линейной и полифазной интерполяции.
Методика суммирования синусоид
Взаимно некоррелированные сигналы рэлеевского замирания генерируются способом, описанным в [2], где i = 1 соответствует синфазной составляющей, а i = 2 соответствует квадратурной составляющей.
(i) t + startk, n (i)), i = 1,2
Где
Nk указывает количество синусоид, используемых для моделирования одного пути.
i) - дискретная доплеровская частота и вычисляется для каждой синусоидальной составляющей в пределах одного пути.
i) является фазой n-го компонента (i) и является i.i.d. случайная величина, имеющая равномерное распределение по 0,2δ].
t - время процесса замирания.
При моделировании доплеровского спектра Джейкса дискретные доплеровские частоты i) с максимальным сдвигом fmax задаются как
12) + αk, 0 (i)]
где
1,2,..., K
Для ускорения процесса замирания во времени вводится начальный параметр времени tinit. Формы сигнала замирания становятся
n (i)), i = 1,2
Когда tinit = 0, процесс замирания начинается в нулевое время. Положительное значение tinit продвигает процесс замирания относительно нуля времени при сохранении его непрерывности.
Отсчеты замирания канала формируются по алгоритму GMEDS1 [2].
Расчет комплексных коэффициентов
Сложный процесс, получаемый в результате любого способа, , масштабируется для получения правильного среднего коэффициента усиления тракта. В случае канала Рэлея процесс замирания получается следующим образом:
Startkzk
где
ak | 2]
В случае рикского канала процесс замирания получается следующим образом:
LOS, kt + startLOS, k)]
где k - коэффициент Rician K k-го пути, , k - доплеровский сдвиг составляющей линии визирования k-го пути (в Гц), STARTLOS, k - начальная фаза составляющей линии визирования k-го пути (в рад).
На входе в модель канала многолучевого распространения с ограниченной полосой пропускания передаваемые символы должны быть избыточно дискретизированы с коэффициентом, по меньшей мере, равным коэффициенту расширения полосы пропускания, введенному формированием импульсов. Например, если используется формирование импульсов sinc, для которого ширина полосы частот импульсно-формованного сигнала равна скорости передачи символов, то коэффициент расширения полосы частот равен 1, и на входе в канал требуется, по меньшей мере, одна выборка на символ. Если используется фильтр с увеличенным косинусом (RC) с коэффициентом больше 1, для которого ширина полосы импульсно-образного сигнала равна удвоенной скорости передачи символов, то коэффициент расширения полосы пропускания равен 2, и на входе в канал требуются, по меньшей мере, две выборки на символ.
Канальный фильтр реализует полосовой фильтр с дробной задержкой (FD) с конечной импульсной характеристикой (FIR) с длиной 16 коэффициентов для каждой возможной дробной задержки при 0, 0,02, 0,04,..., 0,98.
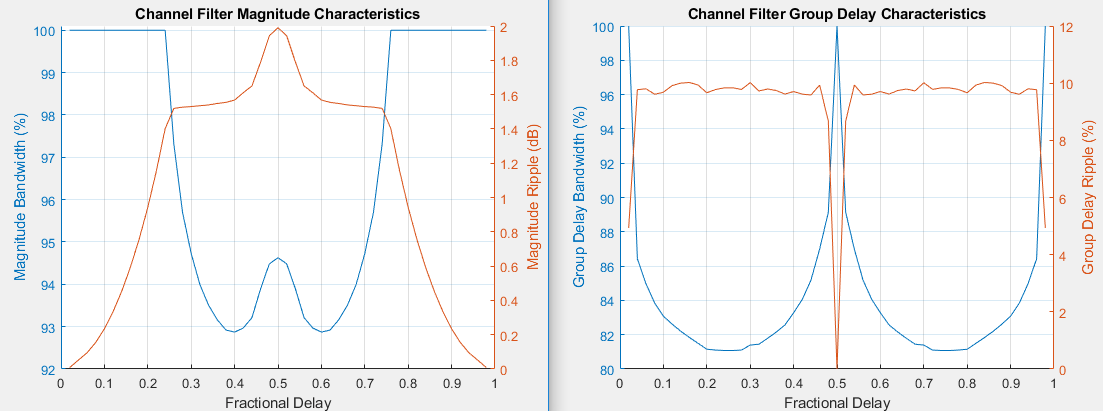
Каждый дискретный тракт округляется до его ближайшей возможной дробной задержки, так что предел ошибки задержки составляет 1% времени выборки. Для достижения полосы пропускания групповой задержки, превышающей 80%, и полосы пропускания величины, превышающей 90%, алгоритм выбирает оптимальные значения коэффициента КИХ для каждой дробной задержки, удовлетворяя при этом следующим критериям:
Пульсация задержки группы ≤ 10%
Величина пульсации ≤ 2 дБ
Затухание полосы частот = 3 дБ
На графиках показаны полосы пропускания, удовлетворяющие критериям проектирования для пульсации групповой задержки, пульсации величины и ослабления полосы частот.
[1] Джерухим, М. К., Балабан, П. и Шанмуган, К. С., Симуляция коммуникационных систем, второе издание, Нью-Йорк, Kluwer Academic/Plenum, 2000.
[2] Пятцольд, Матиас, Чэн-Сян Ван и Бьорн Олав Хогстанд. «Два новых метода, основанных на сумме синусоид, для эффективного генерирования множественных некоррелированных волн релейного замирания». Транзакции IEEE по беспроводной связи. Том 8, номер 6, 2009, стр. 3122-3131.
Communications Toolbox моделирует канал замирания как линейный фильтр FIR. Фильтрация сигнала с использованием канала замирания включает в себя следующие этапы:
Создайте объект канала, описывающий канал, который требуется использовать. Объект канала - это тип переменной MATLAB, которая содержит информацию о канале, такую как максимальный доплеровский сдвиг.
При необходимости настройте свойства объекта канала в соответствии с вашими потребностями. Например, можно изменить задержки пути или среднее увеличение пути.
Примените объект канала к сигналу с помощью вызова объекта.
В этом разделе описывается, как определять, проверять и управлять объектами канала. Темы:
Чтобы создать объект канала замирания, подходящий для ситуации моделирования, выберите один из этих системных объектов.
| Функция | Объект | Смоделированная ситуация |
|---|---|---|
| Объект канала релейного замирания | Один или несколько основных отраженных путей | |
| Объект канала замирания Rician | Одна прямая линия визирования, возможно, совмещенная с одной или несколькими основными отраженными траекториями |
Например, эта команда создает объект канала, представляющий канал релеевского замирания, который действует на сигнал, дискретизированный на частоте 100000 Гц. Максимальный доплеровский сдвиг канала составляет 130 Гц.
rayChan1 = comm.RayleighChannel('SampleRate',1e5,...
'MaximumDopplerShift',130); % Rayleigh fading channel object
Чтобы узнать, как позвонить rayChan1 объект канала замирания для фильтрации передаваемого сигнала по каналу, см. Использование каналов замирания.
Можно также создать другой объект, продублировав существующий объект, а затем при необходимости скорректировать свойства нового объекта. Для дублирования объекта всегда используйте clone функции, такие как:
rayChan2 = clone(rayChan1); % Copy rayChan1 to create an independent rayChan2.
вместо rayChan2 = rayChan1. clone создает копию rayChan1 который не зависит от rayChan1. Напротив, команда rayChan2 = rayChan1 создает rayChan2 как просто ссылка на rayChan1, так что rayChan1 и rayChan2 всегда имеют неразличимое содержание.
Объект канала имеет многочисленные свойства, которые записывают информацию о модели канала, о состоянии канала, который уже отфильтровал сигнал, и о работе канала над будущим сигналом.
Просмотреть свойства можно следующими способами:
Для просмотра всех свойств объекта канала введите имя объекта в окне команд.
Можно просмотреть свойство объекта канала или присвоить значение переменной, введя имя объекта, за которым следует точка (точка), за которой следует имя свойства.
Свойства объекта канала, доступные для записи, можно изменить следующими способами:
Чтобы изменить значение по умолчанию свойства объекта канала, введите требуемое значение в синтаксис создания объекта.
Чтобы изменить значение записываемого свойства объекта канала, выполните инструкцию назначения, использующую точечную нотацию в объекте канала. Более конкретно, точечная нотация означает выражение, которое состоит из имени объекта, за которым следует точка, за которой следует имя свойства.
Отобразить свойства объекта Rayleigh Channel
Создайте объект канала Рэлея. Отображение объекта для отображения свойств, инициализированных по умолчанию, и свойств, заданных при создании объекта. Вход rayChan отображает все свойства объекта канала. Некоторые значения свойств были назначены при создании объекта, в то время как другие свойства имеют значения по умолчанию. Для получения дополнительной информации об определенных свойствах канала см. справочную страницу для comm.RayleighChannel объект.
rayChan = comm.RayleighChannel('SampleRate',1e5,'MaximumDopplerShift',130); rayChan % View all the properties
rayChan =
comm.RayleighChannel with properties:
SampleRate: 100000
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 130
DopplerSpectrum: [1x1 struct]
Show all properties
g = rayChan.AveragePathGains % Retrieve the AveragePathGains property of rayChang = 0
Настройка свойств объекта Rician Channel
Объект Rician с замиранием канала имеет дополнительное свойство, которое не появляется для объекта Rayleigh с замиранием канала, а именно скаляр KFactor собственность. Для получения дополнительной информации о свойствах канала Rician см. справочную страницу для comm.RicianChannel объект.
Изменение свойств объекта Rician Channel
Создайте объект канала Rician. Настройка по умолчанию для Visualization свойство - 'Off'. Изменение значения по умолчанию на 'Impulse response' формирует график импульсной характеристики выходного сигнала при вызове объекта. На выходе отображается подмножество всех свойств объекта канала. Выбрать all properties для просмотра полного набора свойств для ricChan.
ricChan= comm.RicianChannel; % Create object ricChan.Visualization = 'Impulse response' % Enables the impulse response channel visualization
ricChan =
comm.RicianChannel with properties:
SampleRate: 1
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 3
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1x1 struct]
Show all properties
Некоторые свойства объекта канала связаны друг с другом так, что при изменении значения одного свойства значение другого свойства должно изменяться каким-либо соответствующим образом, чтобы поддерживать согласованность объекта канала. Например, при изменении длины вектора PathDelays, то значение AveragePathGains должен изменяться таким образом, чтобы его длина вектора равнялась длине нового значения PathDelays. Это происходит потому, что длина каждого из двух векторов равна количеству дискретных трактов канала. Дополнительные сведения о связанных свойствах и пример см. в разделе comm.RayleighChannel или comm.RicianChannel.
Определяют доплеровский спектр объекта канала через его DopplerSpectrum собственность. Значение этого свойства должно быть следующим:
Структура доплеровского спектра. В этом случае один и тот же доплеровский спектр применяется к каждому пути объекта канала.
Клеточный массив структур доплеровского спектра той же длины, что и PathDelays векторное свойство. В этом случае доплеровский спектр каждого пути задается соответствующей доплеровской структурой спектра в векторе.
Когда длина вектора PathDelays свойство увеличивается, длина DopplerSpectrum автоматически увеличивается в соответствии с длиной PathDelays, добавляя структуры спектра Джейкса Доплера.
Если длина PathDelays векторное свойство уменьшается, длина DopplerSpectrum автоматически уменьшается в соответствии с длиной PathDelaysпутем удаления последних структур доплеровского спектра.
Структура доплеровского спектра содержит свойства, используемые для характеристики доплеровского спектра, но максимальный доплеровский сдвиг является свойством объекта канала. В этом разделе описывается, как создавать структуры доплеровского спектра и управлять ими, а также как назначать их DopplerSpectrum свойство объектов канала.
Для создания структур доплеровского спектра используйте doppler функция. Единственная цель doppler функция для создания структур доплеровского спектра, используемых для задания значения DopplerSpectrum свойство объектов канала. Выберите один из следующих вариантов:
doppler('Jakes')
doppler('Flat')
doppler('Rounded', ...)
doppler('Bell', ...)
doppler('Asymmetric Jakes', ...)
doppler('Restricted Jakes', ...)
doppler('Gaussian', ...)
doppler('BiGaussian', ...)
Например, гауссов спектр с нормированным (на максимальный доплеровский сдвиг канала) стандартным отклонением 0,1, может быть создан как:
dopp1 = doppler('Gaussian',0.1);Примечание
При создании доплеровской структуры спектра учитывайте следующие зависимости:
Если назначить одну структуру доплеровского спектра DopplerSpectrumвсе пути имеют одинаковый заданный доплеровский спектр.
Если FadingTechnique свойство - 'Sum of sinusoids', DopplerSpectrum должно быть doppler('Jakes');
Если назначить массиву ячеек строки различные структуры доплеровского спектра DopplerSpectrumкаждый тракт имеет доплеровский спектр, заданный соответствующей структурой в матрице ячеек. В этом случае длина DopplerSpectrum должно быть равно длине PathDelays.
Чтобы создать код C, укажите DopplerSpectrum к одной структуре доплеровского спектра.
Создайте структуру доплеровского спектра, указав тип доплеровского спектра как 'Rounded', затем изменить настройки полиномного типа
Создается и отображается округленная структура доплеровского спектра со свойствами по умолчанию, и третий элемент Polynomial поле изменено.
doppRound = doppler('Rounded')doppRound = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.7850]
Отрегулируйте третий коэффициент полинома.
doppRound.Polynomial(3) = 0.825
doppRound = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.8250]
Следует иметь в виду, что можно модифицировать структуру доплеровского спектра до недопустимой конфигурации. Проверка настроек структуры доплеровского спектра выполняется, когда структура используется объектом канала замирания. doppRound структура спектра, определенная выше, является действительной.
ricianCh = comm.RicianChannel('DopplerSpectrum',doppRound)ricianCh =
comm.RicianChannel with properties:
SampleRate: 1
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 3
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 1.0000e-03
DopplerSpectrum: [1x1 struct]
Show all properties
DopplerSpectrum свойство объекта канала может быть изменено путем присвоения ему структуры доплеровского спектра или вектора структур доплеровского спектра.
Этот пример иллюстрирует, как изменить спектр Джейкса Доплера по умолчанию для построенного объекта канала Рэлея на плоский спектр Доплера.
Создание объекта канала Рэлея
Установите частоту дискретизации 9600 Гц и максимальный доплеровский сдвиг 100 Гц.
rayChan = comm.RayleighChannel('SampleRate',9600, 'MaximumDopplerShift',100)
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Изменение доплеровского спектра
Создайте плоскую структуру доплеровского спектра и назначьте ее в rayChan объект.
doppFlat = doppler('Flat')doppFlat = struct with fields:
SpectrumType: 'Flat'
rayChan.DopplerSpectrum = doppFlat
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Flat'
В этом примере показано, как изменить спектр Джейкса Доплера по умолчанию для построенного объекта Rician канала на спектр Гаусса Доплера с нормированным стандартным отклонением 0,3, а затем отобразить DopplerSpectrum и измените значение нормированного стандартного отклонения на 1.1.
Создание объекта канала Rician
Установите частоту дискретизации 9600 Гц, максимальный доплеровский сдвиг 100 Гц и коэффициент К 2.
ricChan = comm.RicianChannel('SampleRate',9600, 'MaximumDopplerShift',100, 'KFactor',2)
ricChan =
comm.RicianChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 2
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Изменение доплеровского спектра
Создайте структуру доплеровского спектра Гаусса с нормированным стандартным отклонением 0,3 и назначьте ее в ricChan объект.
doppGaus = doppler('Gaussian',0.3)doppGaus = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 0.3000
ricChan.DopplerSpectrum = doppGaus
ricChan =
comm.RicianChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
KFactor: 2
DirectPathDopplerShift: 0
DirectPathInitialPhase: 0
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 0.3000
ricChan.DopplerSpectrum.NormalizedStandardDeviation = 1.1; ricChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Gaussian'
NormalizedStandardDeviation: 1.1000
Этот пример иллюстрирует, как изменить спектр Джейкса Доплера по умолчанию построенного объекта трехпутного релеевского канала на массив ячеек различных спектров Доплера, а затем изменить свойства спектра Доплера третьего пути.
Создание объекта канала Рэлея
Установите частоту дискретизации 9600 Гц, максимальный доплеровский сдвиг - 100 Гц, и задайте задержки в тракте 0, 1e-4, и 2.1e-4 seconds.
rayChan = comm.RayleighChannel('SampleRate',9600, 'MaximumDopplerShift',100, 'PathDelays',[0 1e-4 2.1e-4])
rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
rayChan.DopplerSpectrum
ans = struct with fields:
SpectrumType: 'Jakes'
Изменение доплеровского спектра
Укажите DopplerSpectrum свойство как массив ячеек с независимым доплеровским спектром для каждого тракта.
rayChan.DopplerSpectrum = {doppler('Flat') doppler('Flat') doppler('Rounded')}rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: {[1x1 struct] [1x1 struct] [1x1 struct]}
Show all properties
rayChan.DopplerSpectrum{:}ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.7200 0.7850]
Изменить Polynomial для третьего пути.
rayChan.DopplerSpectrum{3}.Polynomial = [1 -1.21 0.7]rayChan =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 1.0000e-04 2.1000e-04]
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: {[1x1 struct] [1x1 struct] [1x1 struct]}
Show all properties
rayChan.DopplerSpectrum{:}ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Flat'
ans = struct with fields:
SpectrumType: 'Rounded'
Polynomial: [1 -1.2100 0.7000]
Прежде чем фильтровать сигнал с помощью объекта канала, убедитесь, что свойства канала имеют подходящие значения для моделируемой ситуации. В этом разделе приведены рекомендации по выбору реалистичных значений, соответствующих потребностям моделирования. Темы:
Синтаксы для просмотра и изменения значений свойств объектов канала описаны в разделе Определение канала замирания.
Вот несколько советов по выбору значений свойств, описывающих реалистичные каналы:
Задержки пути
По соглашению первая задержка обычно устанавливается равной нулю. Первая задержка соответствует первому поступающему пути.
Для среды внутри помещения задержки тракта после первого обычно составляют от 1e-9 секунд до 1e-7 секунд.
Для наружной среды задержки пути после первого обычно составляют от 1e-7 секунд до 1e-5 секунд. Большие задержки в этом диапазоне могут соответствовать, например, району, окруженному горами.
Способность сигнала разрешать дискретные пути связана с его полосой пропускания. Если разность между наибольшей и наименьшей задержками в тракте меньше, чем приблизительно 1% периода символа, то сигнал испытывает канал, как если бы он имел только один дискретный тракт.
Среднее увеличение пути
Средние коэффициенты усиления тракта в объекте канала указывают средний коэффициент усиления мощности каждого тракта замирания. На практике среднее значение усиления тракта является большим отрицательным значением дБ. Однако компьютерные модели обычно используют средние коэффициенты усиления пути в диапазоне [-20, 0] дБ.
Значения дБ в векторе средних коэффициентов усиления пути часто примерно линейно затухают как функция задержки, но конкретный профиль задержки зависит от среды распространения.
Чтобы гарантировать, что ожидаемая общая мощность комбинированного усиления тракта равна 1, можно нормализовать усиление тракта через NormalizePathGains свойство объекта канала.
Максимальные доплеровские сдвиги
Доплеровские сдвиги задаются в терминах относительной скорости между передатчиком и приемником. Максимальный доплеровский сдвиг в Герце, fd = vf ∕ c. В формуле v - относительная скорость в м/с, f - частота несущей передачи в Герце, а c - скорость света (3 × 108 м/с). Относительная скорость является величиной без информации о направлении.
Примените формулу максимального доплеровского сдвига, предполагая частоту несущей передачи 900 МГц, автомобиль, движущийся со скоростью автострады, и пешехода. Сигнал, передаваемый от автомобиля, движущегося со скоростью автострады к стационарному приемнику, будет испытывать максимальный доплеровский сдвиг приблизительно 80 Гц. Сигнал, передаваемый с мобильного телефона, удерживаемого пешеходом, на стационарный приемник, будет испытывать максимальный доплеровский сдвиг приблизительно 4 Гц.
Максимальный доплеровский сдвиг, равный 0, соответствует статическому каналу, который исходит из распределения Рэлея или Рикия.
Доплеровский спектр
K-коэффициент для каналов замирания Rician
Коэффициент Rician K определяет отношение зеркальной мощности к диффузной для прямой линии визирования. Отношение выражается линейно, а не в дБ.
Для замирания Rician коэффициент K обычно находится в диапазоне [1, 10].
Коэффициент К, равный 0, соответствует замиранию Рэлея.
Доплеровское смещение траектории линии визирования (LOS) для каналов замирания Rician
Доплеровский сдвиг траектории Rician LOS, также известный как доплеровский сдвиг прямой траектории, определяет относительное движение траектории LOS между передатчиком и приемником.
Доплеровский сдвиг пути Ricic LOS в Герце, fd_los = (u⋅w) × f ∕ c. В формуле (u⋅w) - скалярное произведение векторов u и w, u - нормализованный путь LOS от передатчика к приёмнику, w - скорость приемника относительно передатчика, f - частота несущей передачи в Герце, c - скорость света (3 × 108 м/с).
Используйте эту формулу для несущей частоты передачи 900 МГц с заданной относительной скоростью. Для сигнала от передатчика с началом координат, который достигает приемника с координатой [100 100 0], где относительная скорость между передатчиком и приемником w = [3 -6 0,1]. Доплеровский сдвиг LOS тракта составляет 4,25 Гц.
Параметры доплеровского спектра
См. раздел doppler справочная страница для соответствующих структур доплеровского спектра для описания параметров и их значимости.
Советы по настройке объекта канала для настройки процесса фильтрации:
Если данные разбиты на последовательность векторов (например, обрабатываемых в цикле), объект канала можно вызвать несколько раз (в каждой итерации в цикле). Информация о состоянии канала обновляется и сохраняется после каждого вызова. Выход канала не имеет отношения к разделению данных (длина вектора).
Если требуется, чтобы выходной сигнал канала был воспроизводимым, выберите опцию начального значения для RandomStream свойство объекта канала. Чтобы повторить вывод, вызовите reset объектная функция для сброса как внутренних фильтров, так и внутреннего генератора случайных чисел.
Если требуется моделировать прерывисто передаваемые данные, установите FadingTechnique свойство для 'Sum of sinusoids' и InitialTimeSource свойство для 'Input port' для объекта канала. При вызове объекта укажите время начала каждого вектора/кадра данных, обрабатываемого каналом через вход.
Если требуется нормализовать процесс замирания таким образом, чтобы ожидаемое значение суммарной мощности усиления тракта составляло 1 (канал не вносит дополнительный прирост или потерю мощности), установите значение NormalizePathGains свойство объекта канала для true.
После создания объекта канала, как описано в разделе Определение канала замирания, можно вызвать объект для передачи сигнала через канал. Предоставьте сигнал в качестве входного аргумента для объекта канала. В конце операции фильтрации объект канала сохраняет свое состояние, чтобы можно было узнать окончательное усиление пути или общее количество выборок, обработанных каналом, путем вызова функции информационного объекта с объектом в качестве входного аргумента.
Пример, иллюстрирующий основной синтаксис и сохранение состояния, см. в разделе Мощность замирающего сигнала.
Для визуализации характеристик канала установите Visualization свойство для 'Impulse response', 'Frequency response', или 'Doppler spectrum'. Дополнительные сведения см. в разделе Визуализация каналов.
В этом примере показано, как визуализировать импульсную характеристику канала.
Создание объекта канала
При создании объекта канала используйте пары имя-значение для установки Visualization собственность
кому 'Impulse response'.
rayChan = comm.RayleighChannel('SampleRate',100000,'MaximumDopplerShift',130,... 'PathDelays',[0 1.5e-5 3.2e-5],'AveragePathGains',[0, -3, -3],... 'Visualization','Impulse response');
Создайте битовый поток и объект модулятора. Модулировать битовый поток и пропускать
модулированный сигнал DBPSK через канал путем вызова объекта канала.
tx = randi([0 1],500,1); dbspkMod = comm.DBPSKModulator; dpskSig = dbspkMod(tx); y = rayChan(dpskSig);

Импульсная характеристика отображается при вызове объекта.
В этих примерах используются каналы замирания:
В этом примере показана мощность замирающего сигнала в зависимости от числа выборок. Он иллюстрирует синтаксис создания и вызова comm.RayleighChannel замирание объекта канала и сохранение состояния объекта канала.
rayChan = comm.RayleighChannel('SampleRate',10000,'MaximumDopplerShift',100); sig = j*ones(2000,1); % Signal out = rayChan(sig); % Pass signal through channel. rayChan % Display all properties of the channel object.
rayChan =
comm.RayleighChannel with properties:
SampleRate: 10000
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 100
DopplerSpectrum: [1x1 struct]
Show all properties
Мощность графика замирания сигнала в зависимости от числа выборок.
plot(20*log10(abs(out)))

В этом примере создается объект канала релеевского замирания с плоской частотой и вызывается для обработки сигнала DBPSK, состоящего из одного вектора. Вычисляют частоту битовых ошибок для различных значений отношения сигнал/шум. Фильтр канала замирания применяется перед AWGN. Эта последовательность рекомендуется использовать при объединении замирания с AWGN.
Создание объектов Rayleigh fading channel, модулятора и демодулятора
chan = comm.RayleighChannel('SampleRate',1e4,'MaximumDopplerShift',100);
Создание модулятора DBPSK и объектов демодулятора с порядком модуляции, равным 2. Создайте модулируемые данные DBPSK и передайте их через канал.
M = 2; % DBPSK modulation order tx = randi([0 M-1],50000,1); % Generate a random bit stream mod = comm.DBPSKModulator; demod = comm.DBPSKDemodulator; dpskSig = mod(tx); fadedSig = chan(dpskSig); % Apply the channel effects
Создайте объект канала AWGN и объект калькулятора частоты ошибок.
awgnChan = comm.AWGNChannel('NoiseMethod', 'Signal to noise ratio (SNR)'); errorCalc = comm.ErrorRate;
Вычислить частоту ошибок для различных значений SNR.
SNR = 0:2:20; % Range of SNR values, in dB. numSNR = length(SNR); berVec = zeros(3, numSNR); % Preallocate a vector for BER results for n = 1:numSNR awgnChan.SNR = SNR(n); rxSig = awgnChan(fadedSig); % Add Gaussian noise rx = demod(rxSig); % Demodulate reset(errorCalc) berVec(:,n) = errorCalc(tx,rx); % Compute error rate. end BER = berVec(1,:);
Вычислите теоретические результаты для сравнения.
BERtheory = berfading(SNR,'dpsk',M,1);Постройте график результатов BER.
semilogy(SNR,BERtheory,'b-',SNR,BER,'r*'); legend('Theoretical BER','Empirical BER'); xlabel('SNR (dB)'); ylabel('BER'); title('Binary DPSK over Rayleigh Fading Channel');

Значение свойства StartFilterDelay объекта канала - это количество выборок, на которое выходной сигнал канала задерживает входной сигнал. При непосредственном сравнении наборов входных и выходных данных необходимо учитывать задержку, используя соответствующие операции усечения или заполнения.
Пример иллюстрирует способ учета задержки перед вычислением частоты битовых ошибок.
Создание модулятора DBPSK и объектов демодулятора с порядком модуляции, равным 2. Создайте модулируемые данные DBPSK и передайте их через канал.
bitRate = 50000;
M = 2; % DQPSK modulation order
mod = comm.DBPSKModulator;
demod = comm.DBPSKDemodulator;
Создание объекта Rayleigh fading channel.
rayChan = comm.RayleighChannel('SampleRate',bitRate,'MaximumDopplerShift',4,... 'PathDelays',[0 0.5/bitRate],'AveragePathGains',[0 -10]); chInfo = info(rayChan); delay = chInfo.ChannelFilterDelay;
Генерировать случайные данные битового потока. Модулируйте данные, пропускайте их через канал замирания и демодулируйте их.
tx = randi([0 M-1],50000,1); dpskSig = mod(tx); fadedSig = rayChan(dpskSig); rx = demod(fadedSig);
Вычисление частоты битовых ошибок с учетом задержки.
errorCalc = comm.ErrorRate('ReceiveDelay', delay);
berVec = step(errorCalc,tx,rx);
ber = berVec(1)ber = 0.0147
num = berVec(2)
num = 737
В этом примере выполняется фильтрация входных данных через канал Rayleigh с замиранием в пределах for цикл. Для создания анимированного эффекта используются небольшие наборы данных из последовательных итераций. Релеевский замирающий канал имеет два дискретных основных пути. Сведения о многократной фильтрации данных по каналу с сохранением непрерывности от одного вызова к другому см. в разделе Настройка объектов канала на основе потребностей моделирования.
Настройка параметров. Укажите скорость передачи в битах 50e3 Гц и число итераций цикла 125. Создайте модулятор QPSK и объекты канала Релея с замиранием.
bitRate = 50000; % Data rate is 50 kb/s numTrials = 125; % Number of iterations of loop M = 4; % QPSK modulation order qpskMod = comm.QPSKModulator; rayChan = comm.RayleighChannel('SampleRate',bitRate,'MaximumDopplerShift',4,'PathDelays',[0 2e-5],'AveragePathGains',[0 -9]);
Инициализируйте график рассеяния.
scatterPlot = comm.ConstellationDiagram;
Применение канала в цикле с сохранением непрерывности. Печать только текущих данных в каждой итерации.
for n = 1:numTrials tx = randi([0 M-1],500,1); % Generate random bit stream pskSig = qpskMod(tx); % PSK modulate signal fadedSig = rayChan(pskSig); % Apply channel effects % Plot the new data from this iteration. update(scatterPlot,fadedSig); end

Обычно усиление тракта в канале с замиранием изменяется незначительно в течение периода 1/(100fd) секунды, где fd - максимальный доплеровский сдвиг. Поскольку этот период соответствует очень большому количеству битов во многих современных беспроводных приложениях данных, оценка производительности в статистически значимом диапазоне замирания канала требует моделирования непомерно большого объема данных. Этот пример иллюстрирует квазистатический подход моделирования канала к сбору статистически значимого количества ошибок. Квазистатическое моделирование каналов обеспечивает более отслеживаемый подход, который можно реализовать с помощью следующих шагов:
Генерация реализации случайного канала с использованием максимального доплеровского сдвига, равного 0.
Обработка большого количества битов.
Вычислить статистику ошибок.
Повторите эти шаги много раз, чтобы получить распределение метрики производительности.
Создание объектов системы модулятора и демодулятора с порядком модуляции 4.
M = 4; dpskMod = comm.DPSKModulator('ModulationOrder',M); dpskDemod = comm.DPSKDemodulator('ModulationOrder',M); numBits = 10000; % Each trial uses 10000 bits numTrials = 20; % Number of BER computations
Как правило, numTrials будет большим числом, чтобы получить точную оценку вероятностей простоев или частоты ошибок пакетов. Использовать 20 здесь, чтобы сделать пример более быстрым.
Создайте объект канала Rician и установите максимальный доплеровский сдвиг равным нулю.
ricianChan = comm.RicianChannel('KFactor',3,'MaximumDopplerShift',0);
В пределах for петлю, генерируют случайный битовый поток, ДФМ модулируют сигнал, фильтруют модулированный сигнал через каналы Rician fading и AWGN и демодулируют замирающий сигнал. Для вычисления частоты ошибок символов для каждого пакета игнорируйте первую выборку из-за начального условия DPSK.
nErrors = zeros(1,numTrials); for n = 1:numTrials tx = randi([0 M-1],numBits,1); % Generate random bit stream dpskSig = dpskMod(tx); % DPSK modulate signal fadedSig = ricianChan(dpskSig); % Apply channel effects rxSig = awgn(fadedSig,15,'measured'); % Add Gaussian noise rx = dpskDemod(rxSig); % Demodulate nErrors(n) = symerr(tx(2:end),rx(2:end)); % Symbol error computation, beginning with sample index 2 end
После for завершение цикла, отображение списка счетчиков ошибок символов в векторе nErrors и вычисление частоты ошибок пакета. Выполнение для выполнения результатов зависит от случайности в примере.
nErrors
nErrors = 1×20
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
per = mean(nErrors > 0) % Proportion of packets that had errorsper = 0.0500
В качестве примера, чтобы показать, как квазистатический подход к моделированию канала может сэкономить вычисления, рассмотрим беспроводную локальную сеть (LAN), в которой несущая частота равна 2,4 ГГц, скорость мобильной связи равна 1 м/с, а скорость передачи битов равна 10 Мбит/с. Следующее выражение показывает, что канал изменяется незначительно по сравнению с 12500 битами:
Mb/s) = 12 500 b
Традиционный подход Монте-Карло для вычисления частоты ошибок этой системы повлечет за собой имитацию тысячи раз, в общей сложности десятки миллионов битов. Напротив, квазистатический подход к моделированию канала будет моделировать несколько пакетов в каждом из примерно 100 местоположений для получения пространственного распределения коэффициентов ошибок. Из этого распределения можно определить, например, насколько надежна линия связи для случайного расположения внутри внутреннего пространства. Если каждое моделирование содержит 5000 битов, 100 моделирований будут обрабатывать полмиллиона битов в целом. Это значительно меньше битов по сравнению с традиционным подходом Монте-Карло.
Эти модели включают использование каналов замирания:
Rayleigh Fading Channel, который иллюстрирует влияние канала на QPSK-модулированный сигнал