Канал AWGN добавляет белый гауссов шум к сигналу, который проходит через него. Создать канал AWGN в модели можно с помощью comm.AWGNChannel object™ системы, блок канала AWGN или awgn функция.
В следующих примерах используется канал AWGN: передатчик и приемник QPSK и общая модуляция QAM в канале AWGN.
Типичные величины, используемые для описания относительной мощности шума в канале AWGN, включают
Отношение сигнал/шум (SNR) на выборку. SNR является фактическим входным параметром для awgn функция.
Отношение энергии битов к спектральной плотности мощности шума (EbN0). Это количество используется BER Analyzer Функции оценки инструментов и производительности на этой панели инструментов.
Отношение энергии символа к спектральной плотности мощности шума (EsN0)
Соотношение между EsN0 и EbN0, выраженное в дБ, является следующим:
10log10 (k)
где k - количество информационных битов на символ.
В системе связи на k может влиять размер алфавита модуляции или кодовая частота кода управления ошибками. Например, в системе, использующей кодовую и 8-PSK модуляцию со скоростью 1/2, количество информационных битов на символ (k) является произведением кодовой скорости и количества кодированных битов на модулированный символ. В частности, (1/2) log2 (8) = 3/2. В такой системе три информационных бита соответствуют шести кодированным битам, которые, в свою очередь, соответствуют двум символам 8-PSK.
Соотношение между EsN0 и SNR, выраженное в дБ, является следующим:
сигналов
где Цым - символьный период сигнала, а Цамп - период дискретизации сигнала.
Для комплексного сигнала основной полосы, избыточно дискретизированного с коэффициентом 4, EsN0 превышает соответствующий SNR на 10 log10 (4).
Деривация для комплексных входных сигналов. Соотношение между EsN0 и SNR для комплексных входных сигналов можно получить следующим образом:
Цым/Цамп) + SNR (дБ)
где
S = мощность входного сигнала, в ваттах
N = Мощность шума, в ваттах
Bn = Полоса пропускания шума, в Герц = Fs = 1/Tsamp.
Fs = частота выборки, в герцах
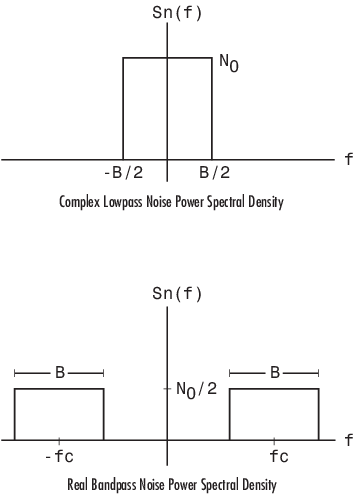
Поведение для реальных и сложных входных сигналов. Эти фигуры иллюстрируют разницу между реальным и комплексным случаями, показывая спектральные плотности мощности шума в реальном полосовом процессе белого шума и его сложный низкочастотный эквивалент.