Этот пример демонстрирует инструменты для классической конструкции управления, пройдя через конструкцию демпфера рыскания для реактивного транспортного самолета 747 ®.
Реактивная модель при крейсерском полете на MACH = 0,8 и H = 40000 футов составляет
A=[-.0558 -.9968 .0802 .0415;
.598 -.115 -.0318 0;
-3.05 .388 -.4650 0;
0 0.0805 1 0];
B=[ .00729 0;
-0.475 0.00775;
0.153 0.143;
0 0];
C=[0 1 0 0;
0 0 0 1];
D=[0 0;
0 0];
sys = ss(A,B,C,D);Следующие команды задают эту модель состояния-пространства как объект LTI и присоединяют имена к состояниям, входам и выходам.
states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw' 'bank angle'};
sys = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);
Можно отобразить модель LTI sys путем ввода sys. Эта команда дает следующий результат.
a =
beta yaw roll phi
beta -0.0558 -0.9968 0.0802 0.0415
yaw 0.598 -0.115 -0.0318 0
roll -3.05 0.388 -0.465 0
phi 0 0.0805 1 0
b =
rudder aileron
beta 0.00729 0
yaw -0.475 0.00775
roll 0.153 0.143
phi 0 0
c =
beta yaw roll phi
yaw 0 1 0 0
bank angle 0 0 0 1
d =
rudder aileron
yaw 0 0
bank angle 0 0
Continuous-time model.Модель имеет два входа и два выхода. Единицы измерения - радианы для beta (угол бокового выступа) и phi (угол банка) и радиан/сек для yaw (скорость рыскания) и roll (скорость крена). Отклонения руля направления и элерона также в радианах.
Вычислите полюса с разомкнутым контуром и постройте их график в s-плоскости.
>> damp(sys)
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-7.28e-03 1.00e+00 7.28e-03 1.37e+02
-5.63e-01 1.00e+00 5.63e-01 1.78e+00
-3.29e-02 + 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
-3.29e-02 - 9.47e-01i 3.48e-02 9.47e-01 3.04e+01
pzmap(sys)
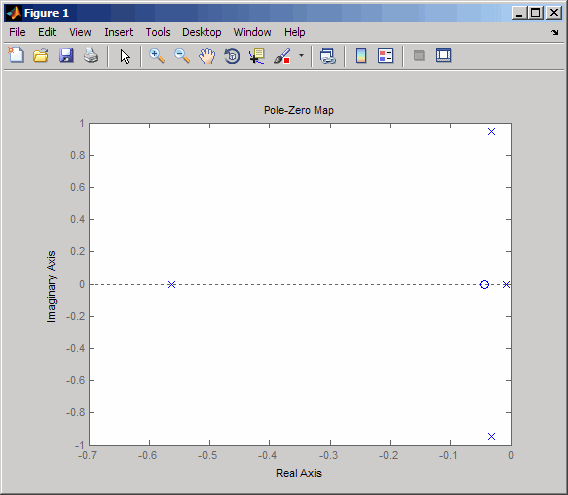
Эта модель имеет одну пару слегка затухающих полюсов. Они соответствуют так называемому «голландскому режиму крена».
Предположим, что Вы хотите проектировать компенсатор, который увеличивает демпфирование этих полюсов, так, чтобы у получающихся сложных полюсов было отношение демпфирования ζ> 0.35 с собственной частотой ωn <1 радиус/секунда. Это можно сделать с помощью инструментов анализа Toolbox™ системы управления.
Во-первых, выполните анализ с разомкнутым контуром, чтобы определить возможные стратегии контроля. Начните с ответа по времени (можно использовать step или impulse здесь).
impulse(sys)
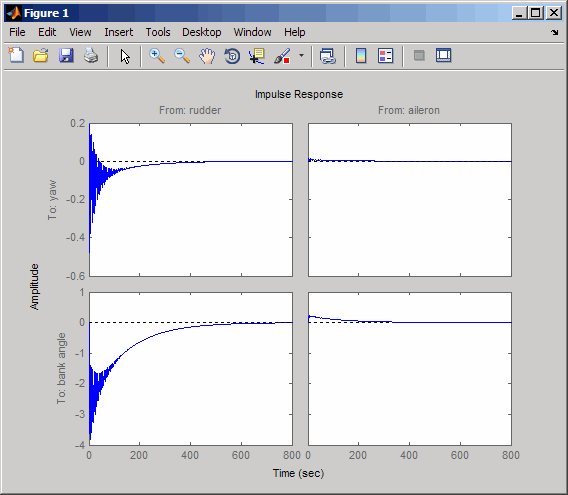
Импульсная характеристика подтверждает, что система слегка затухает. Но временные рамки слишком длинные, потому что пассажиров и пилота больше волнует поведение в течение первых нескольких секунд, а не первых нескольких минут. Следующий взгляд на ответ в течение меньшего промежутка времени 20 секунд.
impulse(sys,20)
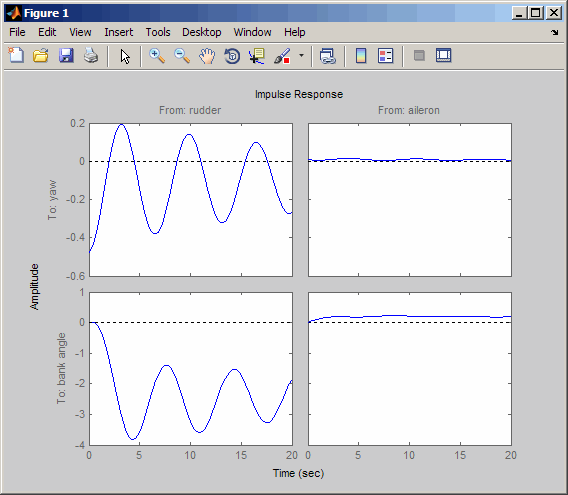
Посмотрите на график от элерона (вход 2) до угла банка (выход 2). Чтобы отобразить только этот график, щелкните правой кнопкой мыши и выберите селектор ввода-вывода, а затем щелкните по записи (2,2). Селектор ввода/вывода должен выглядеть следующим образом.
Новый показатель показан ниже.
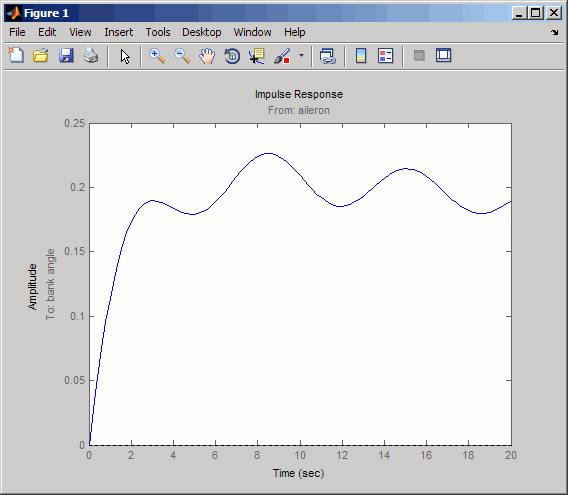
Летательный аппарат колеблется вокруг ненулевого угла крена. Таким образом, самолет поворачивается в ответ на импульс элерона. Это поведение окажется важным позже в данном примере.
Обычно заслонки рыскания проектируются с использованием скорости рыскания в качестве измеряемого выходного сигнала и руля направления в качестве управляющего входного сигнала. Посмотрите на соответствующий частотный отклик.
sys11=sys('yaw','rudder') % Select I/O pair.
bode(sys11)
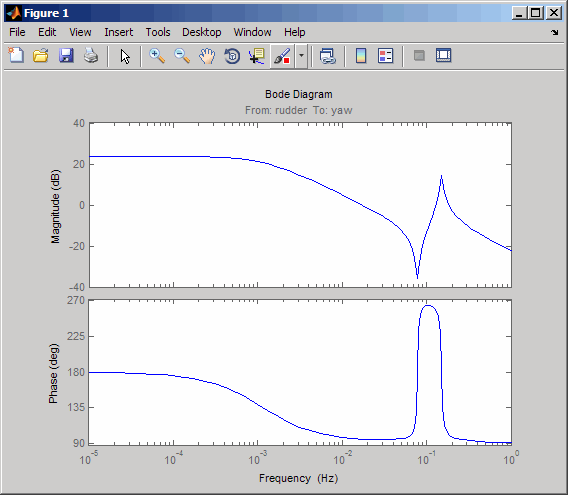
Из этой диаграммы Боде видно, что руль направления оказывает значительное влияние вокруг слегка затухающего голландского режима крена (то есть вблизи λ = 1 рад/сек).
Разумной конструктивной задачей является обеспечение демпфирующего рациона/ 0,35 с собственной частотой/n < 1,0 rad/sec. Поскольку простейшим компенсатором является статический коэффициент усиления, сначала попытайтесь определить соответствующие значения коэффициента усиления с использованием метода корневого локуса.
% Plot the root locus for the rudder to yaw channel rlocus(sys11)

Это корневой локус для отрицательной обратной связи и показывает, что система становится нестабильной почти сразу. Если вместо этого используется положительная обратная связь, система может оставаться стабильной.
rlocus(-sys11) sgrid
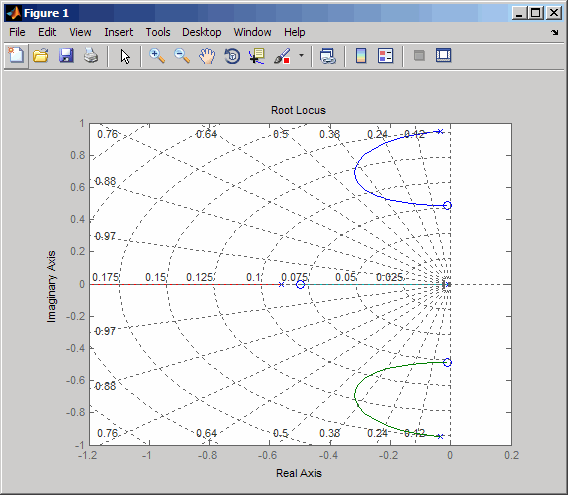
Выглядит лучше. При помощи простой обратной связи Вы можете достигнуть отношения демпфирования ζ> 0.45. Щелкните синюю кривую и переместите маркер данных для отслеживания значений усиления и демпфирования. Для достижения коэффициента демпфирования 0,45 коэффициент усиления должен составлять около 2,85. На этом рисунке показан маркер данных с аналогичными значениями.

Затем закройте контур обратной связи SISO.
K = 2.85;
cl11 = feedback(sys11,-K); % Note: feedback assumes negative
% feedback by default
Постройте график импульсной характеристики с замкнутым контуром в течение 20 секунд и сравните его с импульсной характеристикой с разомкнутым контуром.
impulse(sys11,'b--',cl11,'r',20)
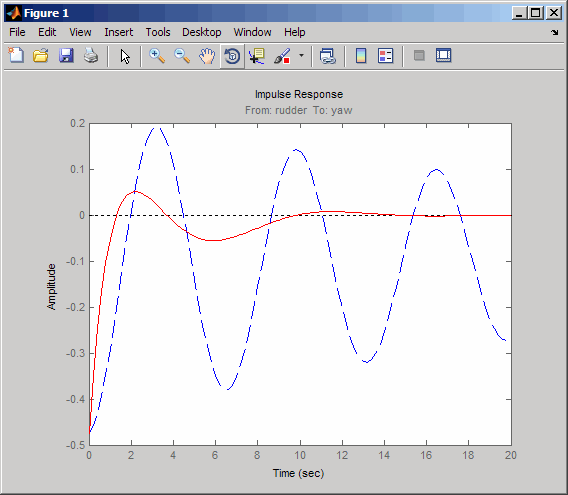
Реакция с замкнутым контуром быстро оседает и не сильно колеблется, особенно по сравнению с реакцией с разомкнутым контуром.
Теперь закройте цикл на полной модели MIMO и посмотрите, как выглядит отклик от элерона. Контур обратной связи включает в себя вход 1 и выход 1 установки (использование feedback с индексными векторами, выбирающими эту пару вход/выход). В подсказке MATLAB ® введите
cloop = feedback(sys,-K,1,1);
damp(cloop) % closed-loop poles
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
-3.42e-01 1.00e+00 3.42e-01 2.92e+00
-2.97e-01 + 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-2.97e-01 - 6.06e-01i 4.40e-01 6.75e-01 3.36e+00
-1.05e+00 1.00e+00 1.05e+00 9.50e-01 Постройте график импульсной характеристики MIMO.
impulse(sys,'b--',cloop,'r',20)
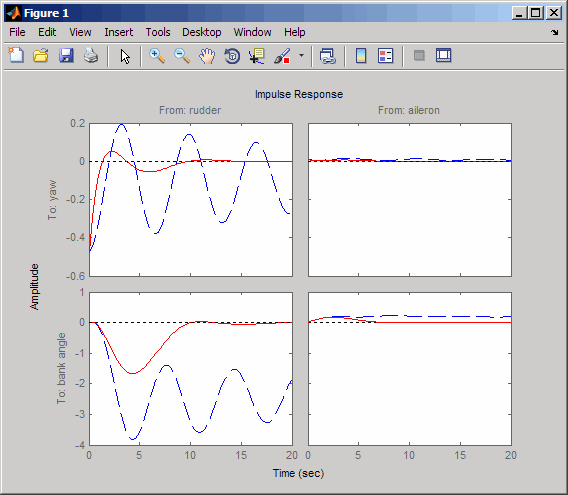
Отклик скорости рыскания теперь хорошо затухает, но посмотрите на график от элерона (вход 2) до угла банка (выход 2). При перемещении элерона система больше не продолжает накапливаться, как обычный самолет. Превышена стабилизация спирального режима. Спиральный режим, как правило, является очень медленным и позволяет самолету подниматься и поворачиваться без постоянного ввода элерона. Пилоты привыкли к такому поведению и не понравятся вашей конструкции, если она не позволит им нормально летать. Эта конструкция перемещает спиральный режим так, что он имеет более высокую частоту.
Необходимо убедиться, что спиральный режим не перемещается дальше в левую половину плоскости при закрытии контура. Одним из способов решения этой проблемы конструкторами управления полетом является использование фильтра для промывки kH, где
ss + α
Фильтр вымывания помещает ноль в начало координат, что ограничивает положение полюса спиральной моды рядом с началом координат. Мы выбираем α = 0.2 для постоянной времени пять секунд и используем метод корневого локуса для выбора усиления фильтра H. Сначала укажите фиксированную часть s/( s + α) вымывания с помощью
H = zpk(0,-0.2,1);
Соедините промывку последовательно с расчетной моделью sys11 (отношение между входом 1 и выходом 1) для получения модели с разомкнутым контуром
oloop = H * sys11;
и нарисуйте другой корневой локус для этой модели с разомкнутым контуром.
rlocus(-oloop) sgrid
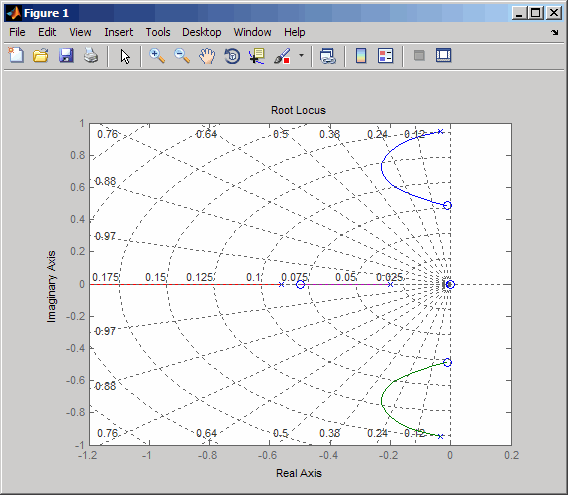
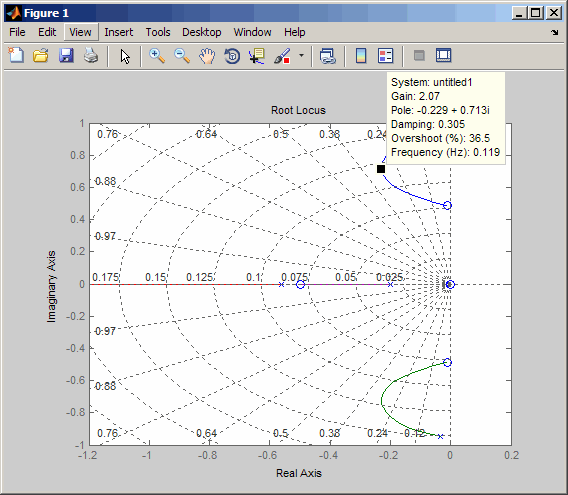
Создайте и тяните маркер данных вокруг верхней кривой, чтобы определить местонахождение максимального демпфирования, которое является о ζ = 0.3.
На этом рисунке показан маркер данных с максимальным коэффициентом демпфирования; коэффициент усиления составляет приблизительно 2,07.
Посмотрите на замкнутую реакцию от руля на скорость рыскания.
K = 2.07; cl11 = feedback(oloop,-K); impulse(cl11,20)
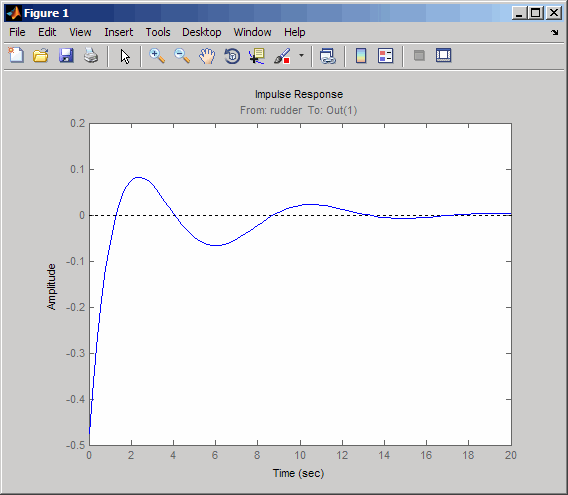
Отклик хорошо оседает, но имеет меньшее демпфирование, чем ваш предыдущий дизайн. Наконец, можно проверить, что фильтр вымывания исправил проблему спирального режима. Сначала формируют полный промывочный фильтр kH (s) (промывка + усиление).
WOF = -K * H;
Затем замкните петлю вокруг первой пары ввода-вывода модели MIMO sys и имитируют импульсную характеристику.
cloop = feedback(sys,WOF,1,1); % Final closed-loop impulse response impulse(sys,'b--',cloop,'r',20)
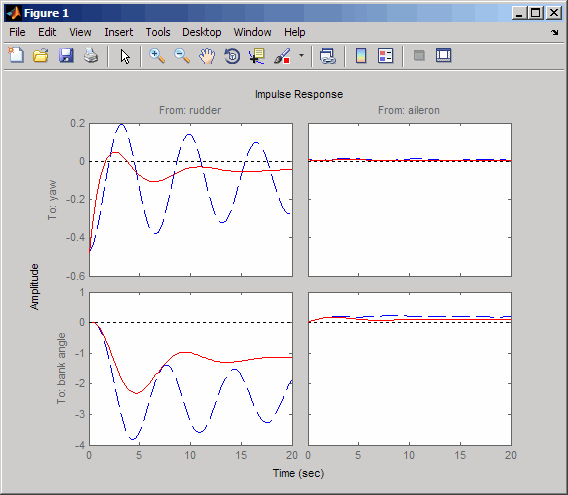
Отклик угла банка (выход 2), обусловленный импульсом элерона (вход 2), теперь имеет желаемое почти постоянное поведение в течение этого короткого временного интервала. Для более тщательного просмотра ответа используйте селектор ввода/вывода в контекстном меню для выбора пары ввода/вывода (2,2).
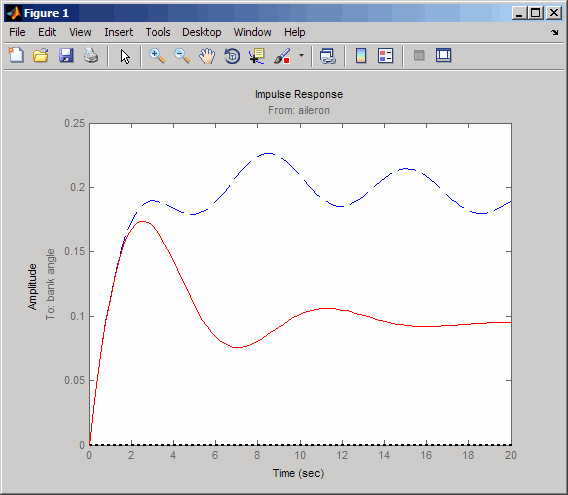
Хотя вы не вполне соответствовали спецификации демпфирования, ваша конструкция существенно увеличила демпфирование системы и теперь позволяет пилоту нормально летать на самолете.