Документация

Параметризация базовой функции

В контроллере, запланированном для усиления, запланированные усиления являются функциями переменных планирования, λ. Например, контроллер PI с планированием усиления имеет вид:

Настройка данного контроллера требует определения функциональных форм _Kp (λ) и _Ki (λ), дающих наилучшую производительность системы в рабочем диапазоне, равном λ. Однако настройка произвольных функций затруднена. Поэтому необходимо либо рассматривать значения функции только в конечном множестве точек, либо ограничивать обобщённость самих функций.

В первом подходе вы выбираете набор расчетных точек, λ, и настраиваете коэффициенты усиления _Kp и _Ki независимо в каждой расчетной точке. Результирующий набор значений коэффициента усиления хранится в таблице поиска, управляемой переменными планирования, λ. Недостатком этого подхода является то, что настройка может давать существенно разные значения для соседних точек проектирования, вызывая нежелательные скачки при переходе от одной рабочей точки к другой.

В качестве альтернативы можно смоделировать выигрыши как гладкие функции, но ограничить обобщённость таких функций, используя определенные расширения базисных функций. Например, предположим, λ является скалярной переменной. Можно смоделировать _Kp (λ) как квадратичную функцию, относящуюся

После настройки это параметрическое усиление может иметь профиль, такой как следующий (специфическая форма кривой зависит от настроенных значений коэффициентов и диапазона, составляющего, в частности, λ):

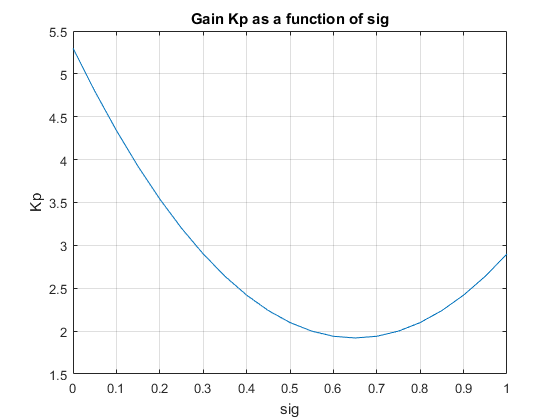
Или предположим, что λ состоит из двух переменных планирования, α и V. Тогда можно моделировать _Kp (λ) как билинейную функцию α и V:

После настройки это параметрическое усиление может иметь следующий профиль. Здесь также специфическая форма кривой зависит от настроенных значений коэффициентов и диапазонов δ значений:

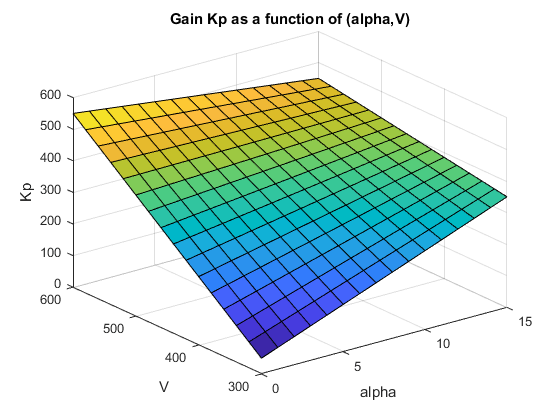
Для настройки графиков усиления с помощью systune, Вы используете параметрическую поверхность выгоды, которая является конкретным расширением выгоды в основных функциях σ:

Базовые функции F1,...,FM выбираемые пользователем и фиксированные. Эти функции работают на n (λ), где n - функция, которая масштабирует и нормализует переменные планирования к интервалу [-1,1] (или заданному интервалу). Коэффициенты расширения, _K0,...,KM, являются настраиваемыми параметрами поверхности усиления. _K0,...,KM может быть скалярным или матрично-значимым, в зависимости от размера ввода-вывода коэффициента усиления K (λ). Выбор базисной функции зависит от проблемы, но в целом сначала попробуйте многочленовые расширения низкого порядка .

Настраиваемые поверхности усиления

Используйте tunableSurface команда для построения настраиваемой модели усиливающей поверхности, дискретизированной по сетке расчетных точек (δ значений). Например, рассмотрим усиление с билинейной зависимостью от двух переменных планирования, α и V:

Предположим, что α - угол падения, который колеблется от 0 ° до 15 °, а V - скорость, которая колеблется от 300 м/с до 700 м/с. Создайте сетку точек проектирования, которые охватывают эти диапазоны. Эти точки проектирования должны соответствовать значениям параметров, при которых производится выборка изменяющегося или нелинейного растения. (См. раздел Модели установки для настройки контроллера по расписанию усиления .)

[alpha,V] = ndgrid(0:5:15,300:100:700);
domain = struct('alpha',alpha,'V',V);

Задайте базовые функции для параметризации этой поверхности, α, V и αV. tunableSurface команда ожидает, что базисные функции будут расположены как вектор функций двух входных переменных. Для выражения базовых функций можно использовать анонимную функцию.

shapefcn = @(alpha,V)[alpha,V,alpha*V];

В качестве альтернативы можно использовать polyBasis, fourierBasis, или ndBasis для создания базисных функций из необходимого количества переменных планирования.

Создайте настраиваемую поверхность с помощью конструктивных точек и базовых функций.

Kp = tunableSurface('Kp',1,domain,shapefcn);

Kp - настраиваемая модель усиливающей поверхности. tunableSurface параметризует поверхность как:

где

Поверхность выражается в терминах нормированных переменных, $$\stackrel{}{}\stackrel{}{}{\mathrm{}\mathrm{}}^{\mathrm{\alpha ¯,V¯\in [-1,1]2}}$$, а не в терминах α и V. Эта нормализация, которая tunableSurface по умолчанию, улучшает кондиционирование оптимизации, выполняемой systune. При необходимости можно изменить масштаб и нормализацию по умолчанию. (см. tunableSurface).

Второй входной аргумент для tunableSurface задает начальное значение постоянного коэффициента, K0. По умолчанию K0 является коэффициентом усиления, когда все переменные планирования находятся в центре своих диапазонов. tunableSurface принимает размеры ввода-вывода усиливающей поверхности от K0. Таким образом, можно создать настраиваемые коэффициенты усиления со значением массива, предоставив массив для этих входных данных.

Karr = tunableSurface('Karr',ones(2),domain,shapefcn);

Karr - матрица 2 на 2, в которой каждая запись является билинейной функцией переменных планирования с независимыми коэффициентами.

Настраиваемое усиление с двумя независимыми переменными планирования

В этом примере показано, как моделировать скалярное усиление K с билинейной зависимостью от двух переменных планирования. Для этого создается сетка точек конструкции, представляющая независимую зависимость двух переменных.

Предположим, что первая переменная α - это угол падения, который находится в диапазоне от 0 до 15 градусов, а вторая переменная V - это скорость, которая находится в диапазоне от 300 до 600 м/с. По умолчанию нормализованные переменные:

Поверхность усиления моделируется как:

где $${}_{\mathrm{}}{}_{\mathrm{K0,...,K3}}$$ - настраиваемые параметры.

Создайте сетку расчетных точек (α, V), которые линейно разнесены в α и V. Эти расчетные точки представляют собой значения переменных планирования, используемые для настройки коэффициентов поверхности усиления. Они должны соответствовать значениям параметров, при которых производится выборка завода.

[alpha,V] = ndgrid(0:3:15,300:50:600);

Эти массивы, alpha и V, представляют независимое изменение двух переменных планирования, каждая из которых проходит через весь диапазон. Поместите их в структуру, чтобы определить точки проектирования для настраиваемой поверхности.

domain = struct('alpha',alpha,'V',V);

Создайте базовые функции, описывающие билинейное расширение.

shapefcn = @(x,y) [x,y,x*y];  % or use polyBasis('canonical',1,2)

В массиве, возвращенном shapefcn, базовыми функциями являются:

Создайте настраиваемую поверхность усиления.

K = tunableSurface('K',1,domain,shapefcn);

Настраиваемую поверхность можно использовать в качестве параметризации для блока таблицы подстановки или блока функции MATLAB в модели Simulink. Или используйте команды взаимодействия модели, чтобы включить ее в качестве настраиваемого элемента в систему управления, смоделированную в MATLAB. После настройки коэффициентов можно исследовать результирующую поверхность усиления, используя viewSurf команда. В этом примере вместо настройки вручную установите коэффициенты на ненулевые значения и просмотрите результирующий коэффициент усиления.

Ktuned = setData(K,[100,28,40,10]);
viewSurf(Ktuned)

viewSurf отображает поверхность усиления как функцию переменных планирования для диапазонов значений, указанных domain и хранится в SamplingGrid свойство поверхности усиления.

Настраиваемые поверхности в Simulink

В модели Simulink графики усиления моделируются с использованием блоков таблицы поиска, блоков MATLAB Function или блоков интерполяции матриц, как описано в разделе Системы управления усилением модели в Simulink. Чтобы настроить эти поверхности усиления, используйте tunableSurface для создания поверхности усиления для каждого блока. В slTuner интерфейс с моделью, обозначить каждую спецификацию усиления как блок для настройки и задать ее параметризацию для соответствующей поверхности усиления. Например, rct_CSTR модель включает контроллер PI с планированием усиления, Concentration controller подсистема, в которой коэффициенты усиления Kp и Ki варьируются в зависимости от переменной планирования Cr.

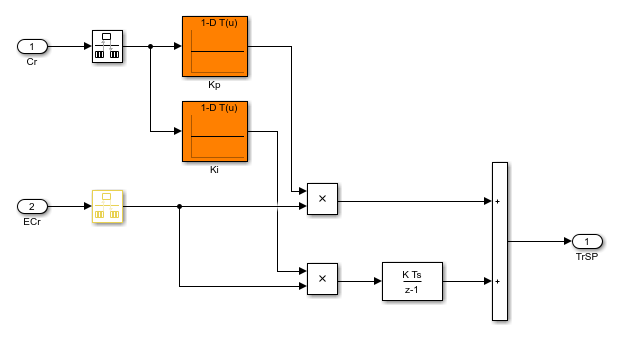
Настройка таблиц подстановки Kp и Kiсоздайте настраиваемую поверхность для каждой из них. Предположим, что CrEQ является вектором точек проектирования, и ожидается, что коэффициенты усиления будут изменяться квадратично с Cr.

TuningGrid = struct('Cr',CrEQ);
ShapeFcn = @(Cr) [Cr , Cr^2];

Kp = tunableSurface('Kp',0,TuningGrid,ShapeFcn);
Ki = tunableSurface('Ki',-2,TuningGrid,ShapeFcn);

Предположим, что у вас есть массив Gd линеаризаций подсистемы установки, CSTR, в каждой из точек проектирования в CrEQ. (См. раздел «Заводские модели для настройки контроллера усиления по расписанию»). Создание slTuner интерфейс, заменяющий этот массив для подсистемы установки и обозначающий два блока таблицы поиска для настройки.

BlockSubs = struct('Name','rct_CSTR/CSTR','Value',Gd);
ST0 = slTuner('rct_CSTR',{'Kp','Ki'},BlockSubs);

Наконец, используйте настраиваемые поверхности для параметризации таблиц подстановки.

ST0.setBlockParam('Kp',Kp);
ST0.setBlockParam('Ki',Ki);

Когда настраиваешься STO, systune настраивает коэффициенты настраиваемых поверхностей Kp и Ki, так что каждая настраиваемая поверхность представляет настроенное соотношение между Cr и выигрыш. Когда настроенные значения записываются обратно в блок для проверки, setBlockParam автоматически создает настроенные данные таблицы подстановки путем оценки настраиваемых поверхностей в точках останова, указанных в соответствующих блоках.

Дополнительные сведения об этом примере см. в разделе Управление химическим реактором по расписанию усиления.

Настраиваемые поверхности в MATLAB

Для системы управления, смоделированной в MATLAB ®, используйте настраиваемые поверхности для создания более сложных элементов управления с планированием усиления, таких как контроллеры PID с планированием усиления, фильтры или контроллеры пространства состояний. Например, предположим, что создаются две поверхности усиленияKp и Ki использование tunableSurface. Следующая команда создает настраиваемый PI-контроллер с планированием усиления.

C0 = pid(Kp,Ki);

Аналогично, предположим, что создаются четыре матричные поверхности усиления A, B, C, D. Следующая команда создает настраиваемый контроллер состояния-пространства с планированием усиления.

C1 = ss(A,B,C,D);

Затем контроллер с запланированным коэффициентом усиления включается в обобщенную модель всей системы управления. Например, предположим G - массив моделей вашего завода, отобранных в точках проектирования, указанных в Kp и Ki. Затем следующая команда создает настраиваемую модель системы управления PID с одним контуром с планированием усиления.

T0 = feedback(G*C0,1);

При соединении настраиваемой поверхности с другими моделями LTI результирующая модель представляет собой массив настраиваемых обобщенных genss модели. Расчетные точки настраиваемой поверхности определяют размеры массива. Таким образом, каждая запись в массиве представляет систему с соответствующим значением переменной планирования. SamplingGrid свойство массива хранит эти точки конструкции.

T0 = feedback(G*Kp,1)

T0 =

  4x5 array of generalized continuous-time state-space models.
  Each model has 1 outputs, 1 inputs, 3 states, and the following blocks:
    Kp: Parametric 1x4 matrix, 1 occurrences.

Type "ss(T0)" to see the current value, "get(T0)" to see all properties, and
"T0.Blocks" to interact with the blocks.

Полученная обобщенная модель имеет настраиваемые блоки, соответствующие поверхностям усиления, используемым для создания модели. В этом примере система имеет одну усилительную поверхность, Kp, который имеет четыре перестраиваемых коэффициента, соответствующих K0, K1, K2 и K3. Поэтому настраиваемый блок является векторным realp с четырьмя записями.

При настройке системы управления на systuneпрограмма настраивает коэффициенты для каждой из точек проектирования, указанных в настраиваемой поверхности.

Пример, иллюстрирующий весь рабочий процесс в MATLAB, см. в разделе «Настройка контроллера в MATLAB» в разделе Контроль усиления химического реактора.