Аппроксимация по шлицам тензорного изделия

Поскольку панель инструментов может обрабатывать сплайны с векторными коэффициентами, легко реализовать интерполяцию или аппроксимацию к данным с сеткой с помощью тензорных сплайнов произведения, как показано на следующей иллюстрации. Можно также выполнить пример «Двухмерные тензорные шлицы продукта».

Конечно, большая часть аппроксимации сплайна тензорного произведения к данным с сеткой может быть получена непосредственно с помощью одной из команд построения сплайна, например spapi или csape, в этой панели инструментов без учета деталей, рассмотренных в этом примере. Скорее, этот пример предназначен для иллюстрации теории, лежащей в основе конструкции тензорного изделия, и это будет полезно в ситуациях, не охваченных командами конструирования в этой панели инструментов.

В этом разделе рассматриваются следующие аспекты задачи, связанной со сплайном тензорного изделия:

Выбор площадок и узлов

Рассмотрим, например, приближение наименьших квадратов к заданным данным z (i, j) = f (x (i), y (j)), i = 1: Nx, j = 1: Ny. Вы берете данные из функции, широко используемой Франке для тестирования схем для подгонки поверхности (см. Р. Франке, «Критическое сравнение некоторых методов интерполяции разрозненных данных», Военно-морская аспирантура Техник. Rep. NPS-53-79-003, март 1979). Его доменом является единичный квадрат. Вы выбираете еще несколько сайтов данных в направлении x, чем в направлении y; кроме того, для лучшего определения используется более высокая плотность данных вблизи границы.

x = sort([(0:10)/10,.03 .07, .93 .97]);
y = sort([(0:6)/6,.03 .07, .93 .97]);
[xx,yy] = ndgrid(x,y); z = franke(xx,yy);

Аппроксимация наименьших квадратов как функция y

Рассматривайте эти данные как поступающие из векторнозначной функции, а именно функции y, значение y (j) которой является вектором z (:, j), все j. Без особых причин выберите аппроксимацию этой функции векторно-значимым параболическим сплайном с тремя равномерно расположенными внутренними узлами. Это означает, что порядок сплайна и последовательность узлов для этого сплайна с векторными значениями выбираются как

ky = 3; knotsy = augknt([0,.25,.5,.75,1],ky);

а затем использовать spap2 для получения наименьших квадратов, аппроксимирующих данные:

sp = spap2(knotsy,ky,y,z);

Фактически, вы находите одновременно дискретное приближение наименьших квадратов от S_ky,knotsy каждому из Nx наборы данных

$\begin{matrix} {(y (j), z (i,}_{j)}^{)} j & = 1Ny \end{matrix}$ , i = 1: Nx

В частности, заявления

yy = -.1:.05:1.1;
vals = fnval(sp,yy);

предоставить массив vals, чья запись vals(i,j) может быть принято за приближение к значению f (x (i), yy (j)) базовой функции f в точке сетки x (i), yy (j), посколькуvals(:,j) - значение в yy (j) аппроксимирующей сплайновой кривой вsp.

Это видно на следующем рисунке, полученном командой:

mesh(x,yy,vals.'), view(150,50)

Обратите внимание на использование vals.', в mesh , требуется из-за матрично-ориентированного вида MATLAB ® при печати массива. Это может быть серьезной проблемой в двухмерном приближении, потому что там принято считать z (i, j) значением функции в точке (x (i), y (j)), в то время как MATLAB думает о z (i, j) как значении функции в точке (x (j), y (i)).

Семейство гладких кривых, притворяющихся поверхностью

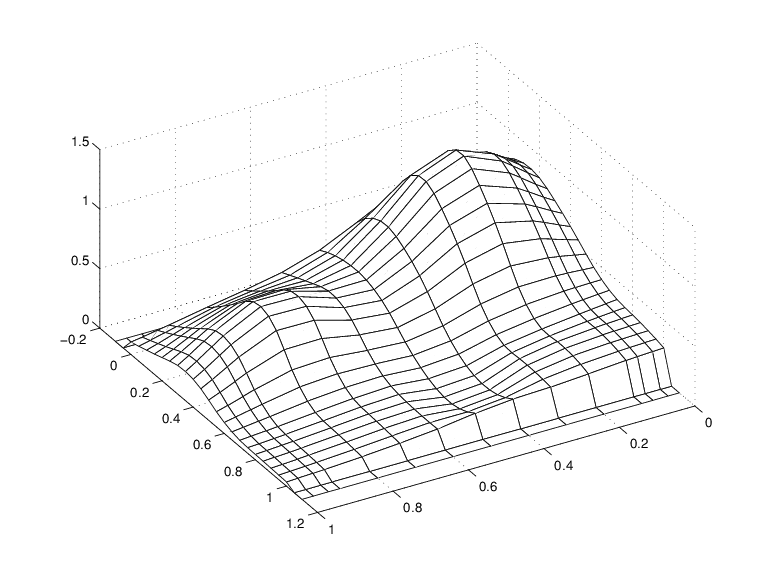
Обратите внимание, что и первые два, и последние два значения на каждой гладкой кривой фактически равны нулю, потому что и первые два, и последние два участка в yy находятся вне базового интервала для сплайна в sp.

Обратите внимание также на гребни. Они подтверждают, что гладкие кривые выводятся только в одном направлении.

Аппроксимация коэффициентов как функций x

Чтобы получить фактическую поверхность, теперь нужно пойти на шаг дальше. Посмотрите на коэффициенты coefsy сплайна в sp:

coefsy = fnbrk(sp,'coefs');

Абстрактно, вы можете думать о сплайне в sp в качестве функции

$\underset{}{} y|→∑rcoefsy (:, r_{) Br},$ ky (y)

с i-ой записью coefsy(i,r) векторного коэффициента coefsy(:,r) соответствует x (i), для всех i. Это предполагает аппроксимацию каждого вектора коэффициентаcoefsy(q,:) сплайном того же порядка kx и с той же соответствующей последовательностью узлов knotsx. Без особых причин на этот раз используют кубические шлицы с четырьмя равномерно расположенными внутренними узлами:

kx = 4; knotsx = augknt([0:.2:1],kx); 
sp2 = spap2(knotsx,kx,x,coefsy.');

Обратите внимание, что spap2(knots,k,x,fx) ожидает fx(:,j), чтобы быть опорным в x(j), т.е. ожидает каждый столбец из fx является значением функции. Подгонка опорного элемента coefsy(q, :) при x (q), для всех q, присутствующихspap2 с транспонированием coefsy.

Двумерное приближение

Теперь рассмотрим транспонирование коэффициентов cxy результирующей сплайновой кривой:

coefs = fnbrk(sp2,'coefs').';

Обеспечивает двухмерную аппроксимацию сплайна

$(x, y) \underset{}{} \underset{}{} |→∑q∑rcoefs (q,_{r)} Bq,_{kx (} x)$ Br, ky (y)

к исходным данным

$(x (i), y (j)) |→z (x (i), y (j)), i =$ 1: Nx, j = 1: Ny

Печать этой сплайновой поверхности над сеткой, например сеткой

xv = 0:.025:1; yv = 0:.025:1;

можно выполнить следующие действия:

values = spcol(knotsx,kx,xv)*coefs*spcol(knotsy,ky,yv).'; 
mesh(xv,yv,values.'), view(150,50);

Это приводит к следующему рисунку.

Аппроксимация сплайна к функции Франке

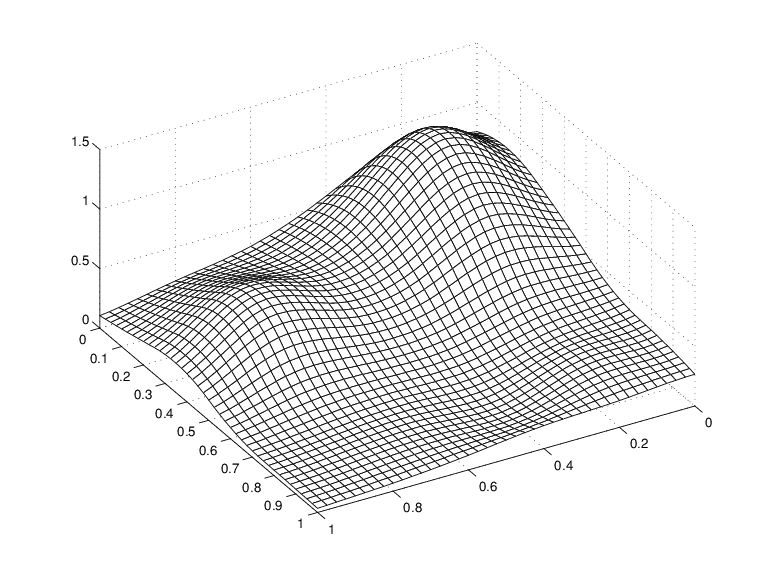
Это имеет хороший смысл, потому что spcol(knotsx,kx,xv) является матрицей, чья (i, q) -я запись равна значению _Bq, kx (xv (i)) на xv (i) qth B-сплайна порядкаkx для последовательности узлов knotsx.

Потому что матрицы spcol(knotsx,kx,xv) и spcol(knotsy,ky,yv) banded, он может быть более эффективным, хотя, возможно, более занимающим память, для больших xv и yv для использования fnval, следующим образом:

value2 = ... 
  fnval(spmak(knotsx,fnval(spmak(knotsy,coefs),yv).'),xv).';

Это, на самом деле, то, что происходит внутри, когда fnval вызывается непосредственно со сплайном тензорного произведения, как в

value2 = fnval(spmak({knotsx,knotsy},coefs),{xv,yv});

Ниже приводится расчет относительной ошибки, т.е. разности между заданными данными и значением аппроксимации в этих узлах данных по сравнению с величиной заданных данных:

errors = z - spcol(knotsx,kx,x)*coefs*spcol(knotsy,ky,y).'; 
disp( max(max(abs(errors)))/max(max(abs(z))) )

Выходные данные: 0.0539, возможно, не слишком впечатляет. Однако массив коэффициентов имел только размер 8 6

disp(size(coefs))

для соответствия массиву данных размера 15 11.

disp(size(z))

Переключение по порядку

Подход, использованный здесь, выглядит предвзятым, следующим образом. Сначала подумайте о данных z как описывающая векторнозначную функцию y, а затем обрабатывающая матрицу, образованную векторными коэффициентами аппроксимирующей кривой, как описывающая векторнозначную функцию x.

Что происходит, когда вы принимаете вещи в противоположном порядке, то есть думаете о z как описывающая векторнозначную функцию x, а затем рассматривающая матрицу, составленную из векторных коэффициентов аппроксимирующей кривой, как описывающая векторнозначную функцию y

Возможно, удивительно, что окончательное приближение то же самое, вплоть до раунда. Вот численный эксперимент.

Аппроксимация наименьших квадратов как функция x

Сначала поместите сплайновую кривую в данные, но на этот раз с x в качестве независимой переменной, следовательно, это строки z теперь они становятся значениями данных. Соответственно, необходимо поставить z.', а не zКому spap2,

spb = spap2(knotsx,kx,x,z.');

таким образом получают сплайновую аппроксимацию для всех кривых (x; z (:, j)). В частности, заявление

valsb = fnval(spb,xv).';

предоставляет матрицу valsb, чья запись valsb(i, j) может быть принято за приближение к значению f (xv (i), y (j)) нижележащей функции f в точке сетки (xv (i), y (j)). Это видно, когда вы строите графикvalsb использование mesh:

mesh(xv,y,valsb.'), view(150,50)

Другое семейство гладких кривых, притворяющихся поверхностью

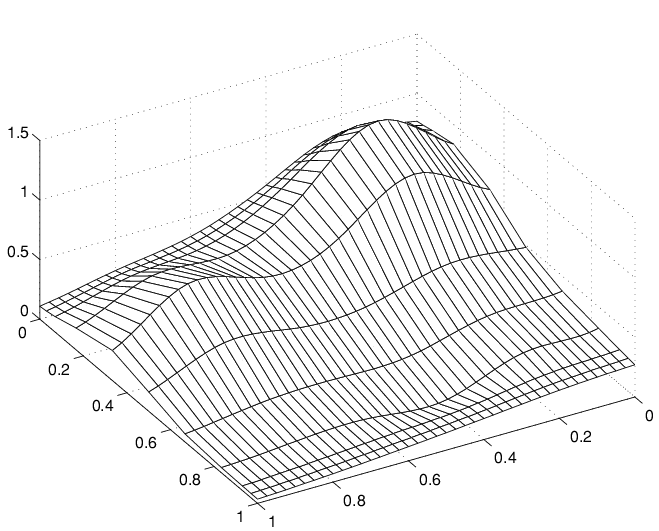
Обратите внимание на гребни. Они подтверждают, что вы снова строите гладкие кривые только в одном направлении. Но на этот раз кривые проходят в другом направлении.

Приближение к коэффициентам как функции y

Теперь идет второй шаг, чтобы получить фактическую поверхность. Сначала извлеките коэффициенты:

coefsx = fnbrk(spb,'coefs');

Затем подгоните каждый вектор коэффициентов coefsx(r,:) сплайном того же порядка ky и с той же соответствующей последовательностью узлов knotsy:

spb2 = spap2(knotsy,ky,y,coefsx.');

Обратите внимание, что снова необходимо транспонировать массив коэффициентов из spb, потому что spap2 принимает столбцы последнего входного аргумента в качестве значений данных.

Соответственно, теперь нет необходимости транспонировать матрицу коэффициентов. coefsb результирующей кривой:

coefsb = fnbrk(spb2,'coefs');

Двумерное приближение

Претензия заключается в том, что coefsb равняется более раннему массиву коэффициентов coefs, вплоть до раунда, и вот тест:

disp( max(max(abs(coefs - coefsb))) )

Выходные данные: 1.4433e-15.

Объяснение достаточно простое: Коэффициенты c сплайна s, содержащегося в sp = spap2(knots,k,x,y) линейно зависят от входных значений y. Это подразумевает, учитывая, что оба c и y 1-строчные матрицы, что существует некоторая матрица A = _Aknots,k, x, так что

$c =_{yAknots,}$ k, x

для любых данных y. Это утверждение даже имеет место, когда y является матрицей, размером d-на-N, скажем, в этом случае каждый опорный элемент y (:, j) принимается как точка в Rd, и полученный сплайн соответственно имеет d-векторное значение, следовательно, его массив коэффициентовc имеет размер d-by-n, с n = length(knots)-k.

В частности, заявления

sp = spap2(knotsy,ky,y,z); 
coefsy =fnbrk(sp,'coefs');

предоставить нам матрицу coefsy что удовлетворяет

$coefsy =_{z.Aknotsy,}$ ky, y

Последующие вычисления

 sp2 = spap2(knotsx,kx,x,coefsy.'); 
 coefs = fnbrk(sp2,'coefs').';

генерировать массив коэффициентов coefs, что, с учетом двух транспозиций, удовлетворяет

$\begin{matrix} coefs = ((_{zAknotsy,} ky, y_{) '.Aknotsx}, \\ kx,_{x)' = (} Aknotsx,_{kx, x) '.} \end{matrix}$ z.Aknotsy, ky, y

Во втором, альтернативном, расчете сначала выполняется вычисление

 spb = spap2(knotsx,kx,x,z.'); 
 coefsx = fnbrk(spb,'coefs');

следовательно coefsx= z '_{.Aknotsx, kx}, x. Последующий расчет

 spb2 = spap2(knotsy,ky,y,coefsx.');
 coefsb = fnbrk(spb,'coefs');

затем предоставлены

$coefsb = coefsx ._{'.Aknotsy,} ky,_{y = (} Aknotsx, kx,_{x).' .}$ z.Aknotsy, ky, y

Следовательно, coefsb = coefs.

Сравнение и расширение

Второй подход более симметричен, чем первый в том, что транспозиция происходит в каждом вызове spap2 и нигде больше. Этот подход может использоваться для аппроксимации данных с привязкой к сетке в любом числе переменных.

Если, например, данные по трехмерной сетке содержатся в некотором трехмерном массиве v размера [Nx,Ny,Nz], с v(i,j,k) содержащий значение f (x (i), y (j), z (k)), то вы начинаете с

coefs = reshape(v,Nx,Ny*Nz);

Предполагая, что nj = knotsj - kj, для j = x,y,z, то Вы будете действовать следующим образом:

sp = spap2(knotsx,kx,x,coefs.');
coefs = reshape(fnbrk(sp,'coefs'),Ny,Nz*nx);
sp = spap2(knotsy,ky,y,coefs.'); 
coefs = reshape(fnbrk(sp,'coefs'),Nz,nx*ny);
sp = spap2(knotsz,kz,z,coefs.'); 
coefs = reshape(fnbrk(sp,'coefs'),nx,ny*nz);

См. главу 17 PGS или [C. de Boor, «Эффективное компьютерное манипулирование тензорными продуктами», ACM Trans. Math. Software 5 (1979), 173-182; Исправления, 525] для получения более подробной информации. Те же ссылки также ясно показывают, что нет ничего особенного в использовании аппроксимации наименьших квадратов. Любой процесс аппроксимации, включая сплайн-интерполяцию, результирующая аппроксимация которой имеет коэффициенты, линейно зависящие от данных, может быть расширена таким же образом до многомерного процесса аппроксимации к данным с сеткой.

Это именно то, что используется в командах построения сплайна csapi, csape, spapi, spaps, и spap2, когда данные с привязкой к сетке должны быть установлены. Он также используется в fnval, когда сплайн тензорного произведения должен быть вычислен на сетке.

Документация