Документация

Конструкция B-формы

Обычно сплайн строится из некоторой информации, такой как значения функций и/или производных значений, или как приблизительное решение некоторого обычного дифференциального уравнения. Но также можно составить сплайн с нуля, предоставив его последовательность узлов и последовательность коэффициентов команде spmak.

Например, при вводе

sp = spmak(1:10,3:8);

вы поставляете однородную последовательность узлов 1:10 и последовательность коэффициентов 3:8. Поскольку существует 10 узлов и 6 коэффициентов, порядок должен быть 4 (= 10 - 6), т.е. получается кубический сплайн. Команда

fnbrk(sp) 

распечатывает составные части B-формы этого кубического сплайна следующим образом:

knots(1:n+k) 
   1 2 3 4 5 6 7 8 9 10 
coefficients(d,n) 
   3 4 5 6 7 8 
number n of coefficients 
   6 
order k 
   4 
dimension d of target 
   1

Далее, fnbrk может использоваться для отдельной поставки каждой из этих деталей.

Однако функциональная возможность «Фитинг кривой» (Curve Fitting) Toolbox™ «Сплайн» (Spline) заключается в том, что нет необходимости искать эти детали. Вы просто используете sp в качестве аргумента для команд, которые вычисляют, дифференцируют, интегрируют, преобразуют или отображают сплайн, описание которого содержится в sp.

Работа со сплайнами B-формы

Для работы со сплайном доступны следующие команды. Есть spmak и fnbrk чтобы составить сплайн и снова его разобрать. Использовать fn2fm для преобразования из B-формы в ppform. Можно вычислять, дифференцировать, интегрировать, минимизировать, находить нули, выводить на график, уточнять или выборочно экстраполировать сплайн с помощью fnval, fnder, fndir, fnint, fnmin, fnzeros, fnplt, fnrfn, и fnxtr.

Существует пять команд для генерации узловых последовательностей:

Кроме того, существует:

Для отображения сплайновой кривой с заданной двумерной последовательностью коэффициентов и однородной последовательностью узлов используйте spcrv.

Можно также создать собственные команды построения сплайнов, в этом случае необходимо знать следующее. Для построения сплайна, удовлетворяющего некоторым условиям интерполяции или аппроксимации, обычно требуется матрица коллокации, то есть матрица, которая в каждой строке содержит последовательность чисел DrBj_, k (start), то есть производную rth из jth B-сплайна, для всех j, для некоторых r и для некоторого сайта Такая матрица предоставляется spcol. Необязательный аргумент позволяет предоставить эту матрицу spcol в компактной сплайн-почти блок-диагональной форме или в виде разреженной матрицы MATLAB ®. Его можно подавать вslvblk, команда для решения линейных систем с матрицей почти блок-диагональных коэффициентов. Если вам интересно посмотреть, как spcol и slvblk используются в этой панели инструментов, посмотрите на команды spapi, spap2, и spaps.

Кроме того, существуют подпрограммы для построения кубических сплайнов. csapi и csape обеспечивают интерполяцию кубического сплайна в узлах к заданным данным, используя, соответственно, не-а-узел и различные другие концевые условия. Параметрическая кубическая сплайновая кривая через заданные точки предоставляется cscvn. Кубический сглаживающий сплайн построен в csaps.

Пример: сплайновое приближение B-формы к окружности

Еще один простой пример:

points = .95*[0 -1 0 1;1 0 -1 0]; 
sp = spmak(-4:8,[points points]);

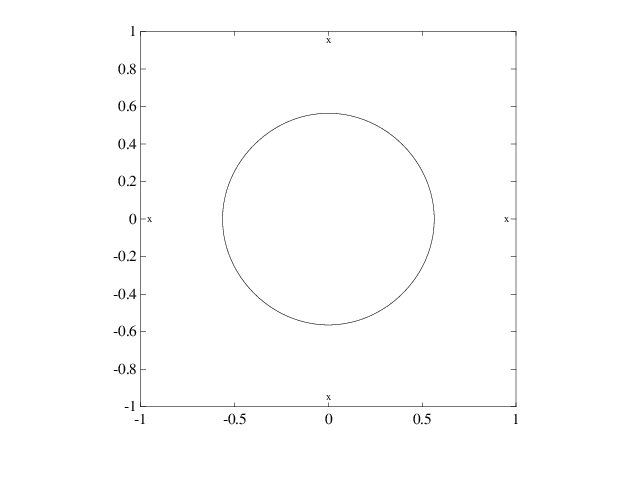
предоставляет плоскую, квартальную, сплайновую кривую, средняя часть которой является довольно хорошим приближением к окружности, как показано на графике на следующей странице. Он генерируется последующим

plot(points(1,:),points(2,:),'x'), hold on 
fnplt(sp,[0,4]), axis equal square, hold off

Вставка дополнительных контрольных точек $$(\pm \mathrm{}0,95,\mathrm{\pm }\sqrt{\mathrm{0,95\; )}}$$/1.9 сделает визуально совершенный круг.

Подробнее. Сформированная сплайновая кривая имеет вид ^Σ8j _{= 1Bj}, 5а (:, j), с -4:8 однородная узловая последовательность и с ее контрольными точками a (:, j) последовательность (0, α), (-α, 0), (0, -α), (α, 0), (0, α), (-α, 0), (0, -α), (α, 0) при α = 0,95. На график выводится только часть кривой между значениями параметров 0 и 4.

Чтобы понять, насколько близка эта часть кривой к круговой, вычислите ее кривизну без знака. Кривизна (t) в точке γ (t) = (x (t), y (t)) пространственной кривой γ может быть вычислена по формуле

где x ', x ″, y' и y "являются первой и второй производными кривой относительно используемого параметра (t). Рассмотрим плоскую кривую как пространственную кривую в плоскости (x, y), таким образом, получите максимум и минимум ее кривизны в 21 точке следующим образом:

t = linspace(0,4,21);zt = zeros(size(t));
dsp = fnder(sp); dspt = fnval(dsp,t); ddspt = fnval(fnder(dsp),t);
kappa = abs(dspt(1,:).*ddspt(2,:)-dspt(2,:).*ddspt(1,:))./...
   (sum(dspt.^2)).^(3/2);
[min(kappa),max(kappa)] 

ans = 
     1.6747    1.8611

Так, хотя кривизна не является достаточно постоянной, она близка к 1/радиусу окружности, как видно из следующего расчета:

1/norm(fnval(sp,0)) 

ans = 
     1.7864