Направленная производная функции
df = fndir(f,y)
df = fndir(f,y) - ppform направленной производной функции f в f, в направлении вектора (column-) y. Это означает, что df описывает функцию f (x) )/t.
Если y является матрицей, с n столбцы, и f d- значение, затем функция в df является prod(d)*n-значение. Его значение при x, видоизмененное, чтобы иметь размер [d,n], имеет в своем j-м «столбце» направленную производную f при x в направлении j-го столбца y. Если вы предпочитаете df чтобы явно отразить фактический размер f, используйте вместо
df = fnchg( fndir(f,y), 'dim',[fnbrk(f,'dim'),size(y,2)] );
С тех пор fndir опирается на ppform функции в f, он не работает ни для рациональных функций, ни для функций в stform.
Например, если f описывает m- варьируемая величина d- векторнозначная функция и x является некоторым моментом в своей области, затем, например, с этой конкретной ppform f который описывает скалярный билинейный многочлен,
f = ppmak({0:1,0:1},[1 0;0 1]); x = [0;0];
[d,m] = fnbrk(f,'dim','var');
jacobian = reshape(fnval(fndir(f,eye(m)),x),d,m)
является якобианом этой функции в этой точке (которая для этой конкретной скалярно-значимой функции является её градиентом, и она равна нулю в начале координат).
В качестве связанного примера, следующие операторы строят градиенты (хорошее приближение к) функции Франке в обычной сетке:
xx = linspace(-.1,1.1,13); yy = linspace(0,1,11);
[x,y] = ndgrid(xx,yy); z = franke(x,y);
pp2dir = fndir(csapi({xx,yy},z),eye(2));
grads = reshape(fnval(pp2dir,[x(:) y(:)].'),...
[2,length(xx),length(yy)]);
quiver(x,y,squeeze(grads(1,:,:)),squeeze(grads(2,:,:)))
Вот получившийся график.
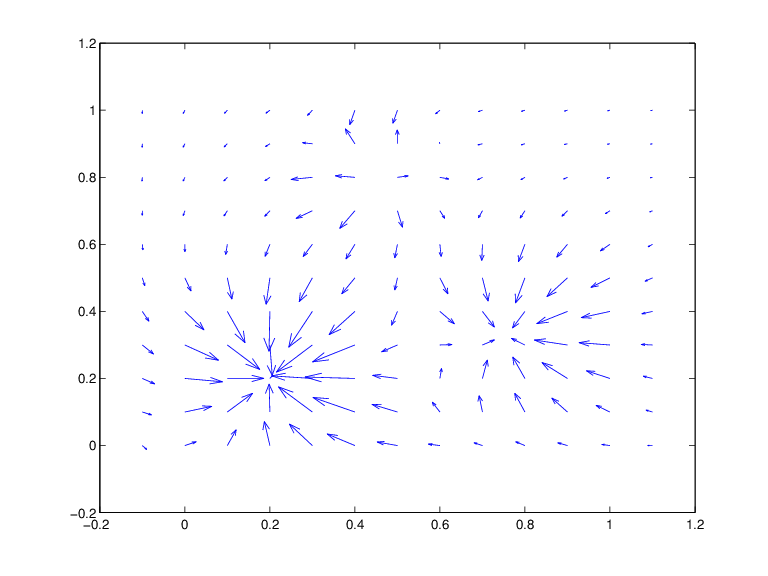
Функция в f преобразуется в ppform, а направленная производная его отрезков многочлена вычисляется формально и в одной векторной операции и снова собирается вместе для формирования ppform направленной производной функции в f.