Интерполяция - это процесс оценки значений, которые лежат между известными точками данных.
Интерполяция включает в себя построение функции f , которая соответствует заданным значениям данных yi в заданных узлах данных xi, в том смысле, что f (xi) = yi, all i.
Интерполянт f обычно строится как уникальная функция формы
) aj
, которая соответствует заданным данным, с функциями fj, выбранными «соответствующим образом».
В сплайновой интерполяции fj выбирается как n последовательных B-сплайнов Bj (x) = B (x 'tj,..., tj + k) , j = 1: n, порядка k для некоторой узловой последовательности t1 ≤ t2 ≤ ... ≤ tn + k.
Метод | Описание |
|---|---|
Линейный | Линейная интерполяция. Этот метод подходит к различным линейным многочленам между каждой парой точек данных для кривых или между наборами из трех точек для поверхностей. |
Ближайший сосед | Интерполяция ближайшего соседа. Этот метод устанавливает значение интерполированной точки на значение ближайшей точки данных. Поэтому этот метод не создает никаких новых точек данных. |
Кубический сплайн | Интерполяция кубического сплайна. Этот метод подходит к различным кубическим многочленам между каждой парой точек данных для кривых или между наборами из трех точек для поверхностей. |
Сохранение формы | Кусочно-кубическая эрмитовая интерполяция (PCHIP). Этот метод сохраняет монотонность и форму данных. Только для кривых. |
Бигармонический (v4) | MATLAB ® 4 Только для поверхностей. |
Тонколистовой шлиц | Тонколистовая сплайновая интерполяция. Этот метод подходит для гладких поверхностей, которые также хорошо экстраполировать. Только для поверхностей. |
Для поверхностей тип посадки Interpolant использует MATLAB scatteredInterpolant для линейных и ближайших методов и MATLAB griddata функция для кубических и бигармонических методов. Метод тонколистового сплайна использует tpaps функция.
Тип используемого интерполятора зависит от характеристик подгоняемых данных, требуемой гладкости кривой, соображений скорости, требований анализа после подгонки и т.д. Линейный и ближайший соседний методы быстры, но результирующие кривые не очень гладкие. Кубический сплайн и методы сохранения формы и v4 медленнее, но результирующие кривые очень гладкие.
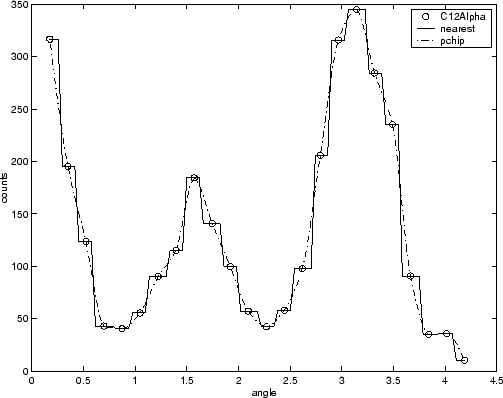
Например, данные ядерной реакции из carbon12alpha.mat здесь показан файл с ближайшей соседней посадкой интерполятора и вставкой интерполятора с сохранением формы (PCHIP). Очевидно, что ближайший соседний интерполятор не следует за данными, а также за сохраняющим форму интерполятором. Разница между этими двумя посадками может быть важна при интерполяции. Тем не менее, если вы хотите интегрировать данные, чтобы получить ощущение общей силы реакции, то обе подгонки дают почти идентичные ответы для разумной ширины ячейки интеграции.
Примечание
Статистика соответствия, пределы прогнозирования и веса не определены для интерполяторов. Кроме того, остатки аппроксимации всегда равны 0 (в пределах компьютерной точности), поскольку интерполяторы проходят через точки данных.
Интерполяторы определяются как кусочные полиномы, поскольку аппроксимируемая кривая строится из множества «кусочков» (за исключением Biharmonic для поверхностей, которые являются интерполяцией радиальной базовой функции). Для кубического сплайна и PCHIP-интерполяции каждый участок описывается четырьмя коэффициентами, которые инструментарий вычисляет с помощью кубического многочлена (третьей степени).
См. раздел spline для получения дополнительной информации о интерполяции кубических сплайнов.
См. раздел pchip для получения дополнительной информации о интерполяции с сохранением формы и для сравнения двух методов.
См. раздел scatteredInterpolant, griddata, и tpaps для получения дополнительной информации о интерполяции поверхности.
К данным можно подогнать один «глобальный» полином-интерполятор, степень которого на единицу меньше числа точек данных. Однако такая посадка может иметь крайне неустойчивое поведение между точками данных. В противоположность этому, кусочные многочлены, описанные здесь, всегда создают хорошо работающую подгонку, поэтому они более гибки, чем параметрические многочлены, и могут эффективно использоваться для более широкого диапазона наборов данных.