Построение аппроксиманта наименьших квадратов обычно требует наличия основы для пространства, из которого должны быть аппроксимированы данные. Как показывает пример пространства «естественных» кубических сплайнов, явное построение основы не всегда является простым.
В этом разделе четко указывается, что явная основа фактически не требуется; достаточно иметь некоторые средства интерполяции в некотором смысле из пространства аппроксимантов. Для этого важно, чтобы функции «Фитинг кривой» (Curve Fitting) Toolbox™ «Сплайн» (Spline) поддерживали работу с векторными функциями.
В этом разделе рассматриваются эти аспекты аппроксимации наименьших квадратов «естественными» кубическими сплайнами.
Требуется построить аппроксимацию наименьших квадратов к заданным данным (x,y) из пространства S «натуральных» кубических сплайнов с заданными разрывами b(1) < ...< b(l+1).
Если вы знаете базис, (f1, f2,..., fm), для линейного пространства S всех «натуральных» кубических сплайнов с последовательностью разрывовb, то вы научились находить приближение наименьших квадратов в форме c(1)f1 + c(2)f2 +... + c(m)fm, с вектором c решение методом наименьших квадратов для линейной системы A*c = y, матрица коэффициентов которой задана
A(i,j) = fj(x(i)), i=1:length(x), j=1:m .
Другими словами, c = A\y.
Общее решение, кажется, требует, чтобы вы знали основу. Однако для построения последовательности коэффициентов c, вам нужно знать только матрицу A. Для этого достаточно иметь под рукой базовую карту, а именно функцию F скажем, так, чтобы F(c) возвращает сплайн, заданный определенной взвешенной суммой c(1)f1+c(2)f2+... +c(m)fm. Для, с помощью этого, вы можете получить, для j=1:m, j-й столбец A как fnval(F(ej),x), с ej j-й столбец eye(m), единичная матрица порядка m.
Еще лучше, сплайн-функции панели инструментов «Фитинг кривой» могут обрабатывать векторные функции, поэтому необходимо иметь возможность построения базовой карты. F для обработки векторных коэффициентов c(i) также. Однако, по согласованию, в этой панели инструментов векторнозначный коэффициент является вектором-столбцом, следовательно, последовательность c обязательно является вектором-строкой векторов-столбцов, т.е. матрицей. С этим, F(eye(m)) является векторнозначным сплайном, i-й компонент является базовым элементом fi, i=1:m. Следовательно, предполагая вектор x сайтов данных, которые должны быть вектором строк, fnval(F(eye(m)),x) является матрицей, (i,j)-entry - значение fi в x(j), т.е. транспонирование матрицы A вы ищете. С другой стороны, как только что было указано, ваша базовая карта F ожидает последовательность коэффициентов c быть вектором строки, т.е. транспонировать вектор A\y. Следовательно, предполагая, соответственно, вектор y из значений данных, являющихся вектором строк, можно получить аппроксимацию наименьших квадратов от S к данным (x,y) как
F(y/fnval(F(eye(m)),x))
Конечно, если вы хотите быть готовы к x и y чтобы быть произвольными векторами (одинаковой длины), следует использовать
F(y(:).'/fnval(F(eye(m)),x(:).'))
Что именно требуется для базовой карты F для линейного пространства S «натуральных» кубических сплайнов с последовательностью разрывов b(1) < ... < b(l+1)? Предполагается, что размер этого линейного пространства равен m, карта F должен установить линейное соответствие один к одному между m-векторы и элементы S. Но это именно то, что csape(b, . ,'var') делает.
Чтобы быть явным, рассмотрим следующую функцию F:
function s = F(c) s = csape(b,c,'var');
Для данного вектора c (той же длины, что и b), он обеспечивает уникальный «естественный» кубический сплайн с последовательностью разрыва b, которая принимает значение c(i) в b(i), i=1:l+1. Уникальность ключевая. Это обеспечивает соответствие между векторами. c и результирующий сплайн F(c) является «один к одному». В частности, m равняется length(b). Более того, поскольку значение f (t) функции f в точке t линейно зависит от f, эта уникальность гарантирует, что F(c) линейно зависит от c (потому что c равняется fnval(F(c),b) и обратная инвертируемая линейная карта снова является линейной картой).
Складывая все вместе, вы получаете следующий код
csape(b,y(:).'/fnval(csape(b,eye(length(b)),'var'),x(:).'),... 'var')
для аппроксимации наименьших квадратов «естественными» кубическими сплайнами с последовательностью разрывов b.
Давайте попробуем некоторые данные, данные переписи, скажем, которые предоставляются в MATLAB ® командой
load census
и который снабжает годами, 1790:10:1990, как cdate и значения как pop. Использовать последовательность разрывов 1810:40:1970.
b = 1810:40:1970; s = csape(b, ... pop(:)'/fnval(csape(b,eye(length(b)),'var'),cdate(:)'),'var'); fnplt(s, [1750,2050],2.2); hold on plot(cdate,pop,'or'); hold off
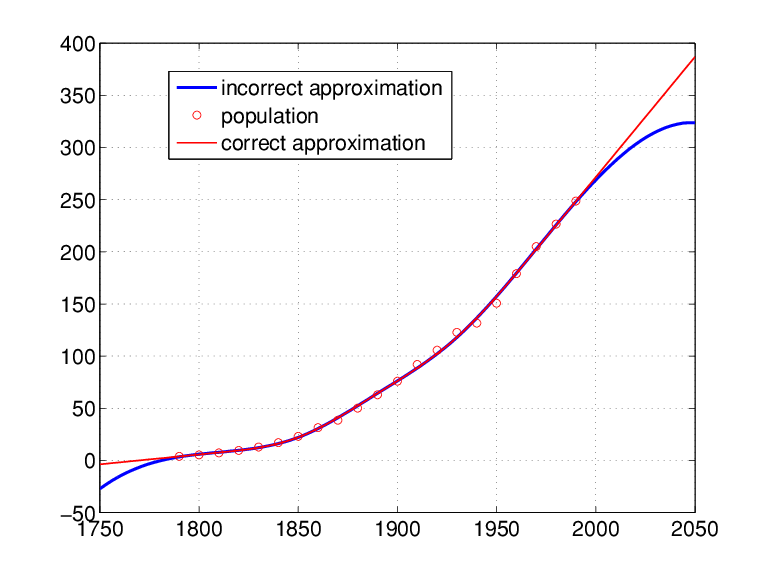
Посмотрите на Хотя-квадраты аппроксимации «естественными» кубическими сплайнами с тремя внутренних разрывов, которые показывают, толстым синим, результирующее приближение, вместе с данными.
Это выглядит как хорошее приближение, за исключением того, что это не похоже на «естественный» кубический сплайн. «Естественный» кубический сплайн, чтобы вспомнить, должен быть линейным слева от своего первого разрыва и справа от своего последнего разрыва, и это приближение не удовлетворяет ни одному условию. Это связано со следующими фактами.
Интерполяция «натурального» кубического сплайна к заданным данным обеспечивается csape в ppform, с интервалом, охватываемым сайтами данных, его базовый интервал. С другой стороны, оценка ppform за пределами его базового интервала выполняется в MATLAB ppval или функция сплайна панели инструментов фитинга кривой fnval, используя соответствующий полиномиальный концевой участок ppform, то есть посредством экстраполяции полного порядка. В случае «естественного» кубического сплайна требуется экстраполяция второго порядка. Это означает, что слева от первого разрыва требуется прямая линия, совпадающая с кубическим сплайном по значению и наклону в первом разрыве. Такая экстраполяция обеспечивается fnxtr. Поскольку «естественный» кубический сплайн имеет нулевую вторую производную при первом разрыве, такая экстраполяция является даже третьей по порядку, т.е. удовлетворяет трем условиям согласования. Таким же образом, за пределами последнего разрыва кубического сплайна, требуется прямая линия, которая согласуется со сплайном по значению и наклону в последнем разрыве, и это тоже предоставляется fnxtr.
Аппроксимация методом наименьших квадратов «естественными» кубическими сплайнами с тремя внутренними разрывами
Следующий однострочный код обеспечивает правильное приближение наименьших квадратов к данным (x,y) «естественными» кубическими сплайнами с последовательностью разрывов b:
fnxtr(csape(b,y(:).'/ ...
fnval(fnxtr(csape(b,eye(length(b)),'var')),x(:).'),'var'))
Но это, надо признать, довольно длинная очередь.
Следующий код использует эту правильную формулу и строит на более тонкой красной линии результирующую аппроксимацию поверх более ранних графиков, как показано в разделе Аппроксимация методом наименьших квадратов с помощью «естественных» кубических сплайнов с тремя внутренними разрывами.
ss = fnxtr(csape(b,pop(:)'/ ...
fnval(fnxtr(csape(b,eye(length(b)),'var')),cdate(:)'),'var'));
hold on, fnplt(ss,[1750,2050],1.2,'r'),grid, hold off
legend('incorrect approximation','population', ...
'correct approximation')
Однолинейное решение отлично работает, если требуется аппроксимировать по пространству S все кубические сплайны с заданной последовательностью разрывов b. Для этого даже не нужно использовать сплайновые функции панели инструментов фитинга кривой, поскольку можно полагаться на MATLAB spline. Вы это знаете, с c последовательность, содержащая на две записи больше, чем b, spline(b,c) предоставляет уникальный кубический сплайн с последовательностью разрывов b которое принимает значение c(i+1) в b(i), все i, и принимает уклон c(1) в b(1)и уклон c(end) в b(end). Следовательно, spline(b,.) является базовой картой для S.
Более того, вы знаете, что spline(b,c,xi) предоставляет значение (значения) вxi этого интерполирующего сплайна. Наконец, вы знаете, что spline может обрабатывать векторные данные. Поэтому следующий однострочный код создает аппроксимацию наименьших квадратов кубическими сплайнами с последовательностью разрывов b к данным (x,y) :
spline(b,y(:)'/spline(b,eye(length(b)),x(:)'))