Объединение функции в Stform
stmak(centers,coefs)
st = stmak(centers,x,type)
st = stmak(centers,coefs,type,interv)
stmak(centers,coefs) возвращает звездочку функции f, заданную
центры (:, j))
с
2log 'x | 2
базисная функция сплайна тонкой пластины и с | x |, обозначающей евклидову норму вектора x.
centers и coefs должны быть матрицами с одинаковым количеством столбцов.
st = stmak(centers,x,type) магазины в st stform функции f, задаваемой
⋅ψj (x)
с, как указано символьным вектором type, которая может быть одной из следующих:
'tp00', для шлица тонкой пластины;
'tp10'для первой производной шлица тонкой пластины относительно его первого аргумента;
'tp01'для первой производной шлица тонкой пластины относительно его второго аргумента;
'tp', значение по умолчанию.
Вот подробности.
| startj (x) = (| x - cj | 2
), cj при (t) = tlog (t) λ n-2 (x) = x (1) λ n-1 (x) = x (2) λ n (x) = 1 |
| startj (x) = (| x - cj | 2
), cj с (t) = (D1t) (logt + 1) и D1t частную производную t = t (x) = | x - cj | 2 относительно x (1) λ n (x) = 1 |
| startj (x) = (| x - cj | 2
), cj с (t) = (D2t) (logt + 1) и D2t частную производную t = t (x) = | x - cj | 2 относительно x (2) λ n (x) = 1 |
| startj (x) = (| x - cj | 2
), cj при (t) = tlog (t) |
st = stmak(centers,coefs,type,interv) также указывает базовый интервал для stform, с interv{j} указание, в форме [a,b], диапазон j-я переменная. Значение по умолчанию для interv - наименьшая такая коробка, содержащая все заданные центры.
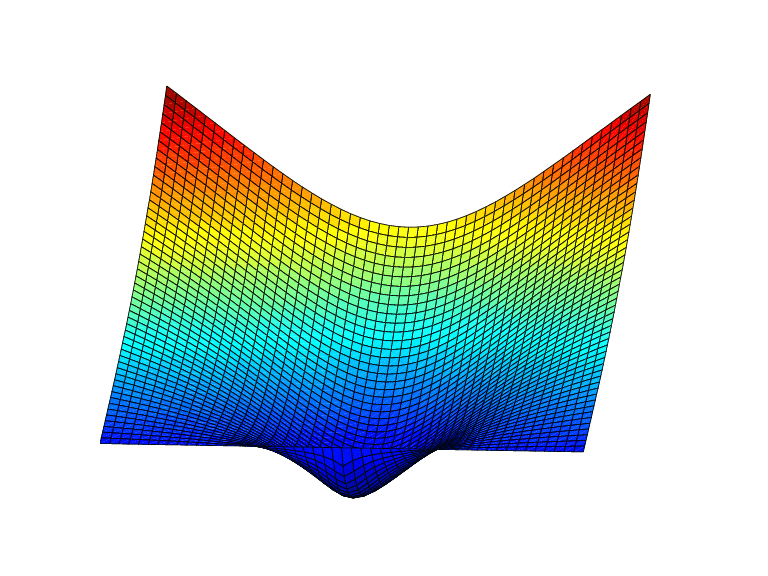
Пример 1. Ниже приведен рисунок базовой функции «тонколистовой сплайн», (2log 'x | 2, но с соответствующим ограничением, чтобы показать, что эта функция отрицательна вблизи начала координат. Для этого существуют дополнительные строки, указывающие нулевой уровень.
inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],1),{inx,iny})
hold on, plot(inx,repmat(linspace(iny(1),iny(2),11),2,1),'r')
view([25,20]),axis off, hold off
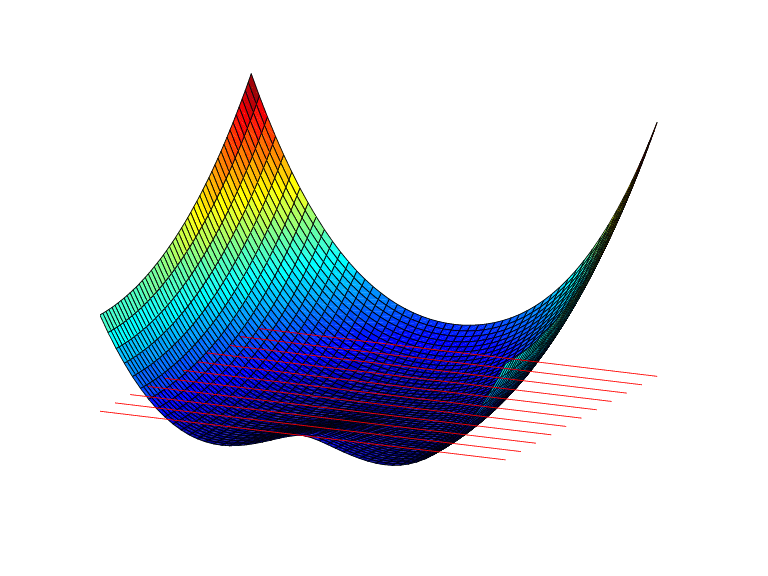
Пример 2. Теперь мы также генерируем и строим график в той же области, что и первая частная производная D2ψ базовой функции сплайна тонкой пластины, относительно ее второго аргумента.
inx = [-1.5 1.5]; iny = [0 1.2];
fnplt(stmak([0;0],[1 0],'tp01',{inx,iny}))
view([13,10]),shading flat,axis off
Обратите внимание, что на этот раз мы явно установили базовый интервал для stform.
Полученный рисунок ниже показывает очень сильное изменение около начала координат. Это отражает тот факт, что там у вторых производных «,» есть логарифмическая сингулярность.