Линейные нейронные сети

Линейные сети, обсуждаемые в этом разделе, аналогичны перцептрону, но их передаточная функция является линейной, а не жестко ограничивающей. Это позволяет их выходам принимать любое значение, тогда как выход перцептрона ограничен либо 0, либо 1. Линейные сети, как и перцептрон, могут решать только линейно разделяемые задачи.

Здесь конструируется линейная сеть, которая при представлении с набором заданных входных векторов производит выходы соответствующих целевых векторов. Для каждого входного вектора можно вычислить выходной вектор сети. Разница между выходным вектором и его целевым вектором является ошибкой. Необходимо найти значения для весов и смещений сети таким образом, чтобы сумма квадратов ошибок была минимизирована или ниже определенного значения. Эта проблема является управляемой, поскольку линейные системы имеют один минимум ошибок. В большинстве случаев линейную сеть можно вычислить непосредственно, так что ее погрешность минимальна для заданных входных и целевых векторов. В других случаях численные проблемы запрещают прямой расчет. К счастью, вы всегда можете обучить сеть иметь минимальную ошибку, используя алгоритм наименьших средних квадратов (Widrow-Hoff).

Этот раздел представляет linearlayer, функция, которая создает линейный слой, и newlindфункция, которая конструирует линейный слой для определенной цели.

Нейронная модель

Линейный нейрон с R входами показан ниже.

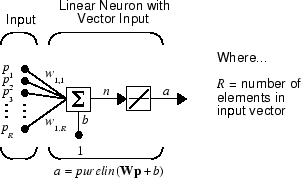
Эта сеть имеет ту же базовую структуру, что и перцептрон. Единственное отличие заключается в том, что линейный нейрон использует линейную передаточную функцию purelin.

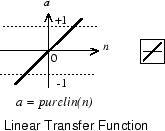
Линейная передаточная функция вычисляет выход нейрона, просто возвращая переданное ему значение.

$α = пурелин (n) = пурелин (Wp +$ b) = Wp + b

Этот нейрон можно обучить изучать аффинную функцию его входов или находить линейное приближение к нелинейной функции. Линейная сеть, конечно, не может быть выполнена для выполнения нелинейных вычислений.

Сетевая архитектура

Линейная сеть, показанная ниже, имеет один уровень S нейронов, соединенных с R входами через матрицу весов W.

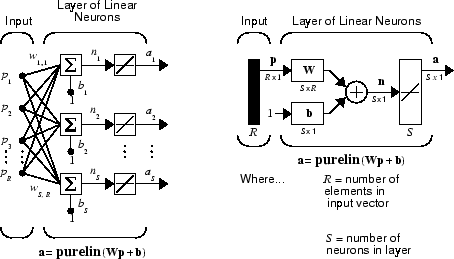
Обратите внимание, что рисунок справа определяет выходной вектор S-длины a.

Показана однослойная линейная сеть. Однако эта сеть так же способна, как и многослойные линейные сети. Для каждой многослойной линейной сети существует эквивалентная однослойная линейная сеть.

Создание линейного нейрона (линейный слой)

Рассмотрим один линейный нейрон с двумя входами. На следующем рисунке показана схема для этой сети.

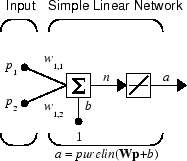
Весовая матрица W в этом случае имеет только одну строку. Выход сети:

$α = пурелин (n) = пурелин (Wp +$ b) = Wp + b

или

$α =_{}_{} {w1,1p1}_{+}_{}$ w1,2p2 + b

Подобно перцептрону, линейная сеть имеет границу принятия решения, которая определяется входными векторами, для которых чистый вход n равен нулю. Для n = 0 уравнение Wp + b = 0 определяет такую границу принятия решения, как показано ниже (адаптировано с благодарностью от [HDB96]).

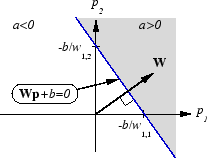
Входные векторы в верхней правой серой области приводят к выходу больше 0. Входные векторы в левой нижней белой области приводят к выходу менее 0. Таким образом, линейная сеть может использоваться для классификации объектов на две категории. Однако классифицировать таким образом можно только в том случае, если объекты являются линейно разделяемыми. Таким образом, линейная сеть имеет те же ограничения, что и перцептрон.

Эту сеть можно создать с помощью linearlayer, и сконфигурировать его размеры с двумя значениями, так что вход имеет два элемента, а выход - один.

net = linearlayer;
net = configure(net,[0;0],0);

Веса сети и смещения по умолчанию равны нулю. Текущие значения можно просмотреть с помощью команд

W = net.IW{1,1}
W =
     0     0

b= net.b{1}
b =
     0

Однако можно присвоить весовые коэффициенты любым требуемым значениям, таким как 2 и 3, соответственно, с помощью

net.IW{1,1} = [2 3];
W = net.IW{1,1}
W =
     2     3

Таким же образом можно установить и проверить смещение.

net.b{1} = [-4];
b = net.b{1}
b =
     -4

Можно смоделировать линейную сеть для определенного входного вектора. Попробуй

p = [5;6];

Вывод сетевого графика можно найти с помощью функции sim.

a = net(p)
a =
    24

Подводя итог, можно создать линейную сеть с помощью linearlayer, отрегулируйте его элементы по своему усмотрению и смоделируйте его с помощью sim.

Наименьшая среднеквадратическая ошибка

Подобно правилу обучения перцептрону, алгоритм наименьшей среднеквадратической ошибки (LMS) является примером контролируемого обучения, в котором правило обучения снабжено набором примеров желаемого поведения в сети:

${_{p1},_{} t1},_{{} {p2}_{,} t2},_{.} . ._{} {$ pQ, tQ}

Здесь pq является входом в сеть, а tq является соответствующим целевым выходом. Когда каждый вход подается в сеть, сетевой выход сравнивается с целевым. Ошибка вычисляется как разница между целевым выходом и сетевым выходом. Цель - минимизировать среднее значение суммы этих ошибок.

$\frac{}{}_{}^{} mse=1Q∑k=1Qe {(k}^{)} \frac{}{}_{}^{} {2=1Q∑k=1Q (t (k) -}^{}$ α (k)) 2

Алгоритм LMS регулирует веса и смещения линейной сети так, чтобы минимизировать эту среднеквадратическую ошибку.

К счастью, индекс среднеквадратической ошибки для линейной сети является квадратичной функцией. Таким образом, индекс производительности будет иметь либо один глобальный минимум, либо слабый минимум, либо никакого минимума, в зависимости от характеристик входных векторов. В частности, характеристики входных векторов определяют, существует ли уникальное решение.

Для получения дополнительной информации по этому вопросу см. главу 10 документа [HDB96].

Проектирование линейной системы (новая линия)

В отличие от большинства других сетевых архитектур, линейные сети могут быть спроектированы непосредственно, если известны пары вектор ввода/целевой вектор. Можно получить определенные значения сетевого графика для весов и смещений, чтобы минимизировать среднеквадратическую ошибку с помощью функции. newlind.

Предположим, что входы и цели

P = [1 2 3];
T= [2.0 4.1 5.9];

Теперь можно проектировать сеть.

net = newlind(P,T);

Можно смоделировать поведение сети, чтобы убедиться, что конструкция выполнена правильно.

Y = net(P)
Y =
    2.0500    4.0000    5.9500

Следует отметить, что сетевые выходы достаточно близки к желаемым целям.

Можно попробовать использовать ассоциацию массива, показывающую поверхность ошибки. Он показывает поверхности ошибок для конкретной задачи, иллюстрирует конструкцию и строит график проектируемого решения.

Также можно использовать функцию newlind для проектирования линейных сетей, имеющих задержки на входе. Такие сети обсуждаются в линейных сетях с задержками. Во-первых, однако, необходимо обсудить задержки.

Линейные сети с задержками

Линия задержки с отводом

Для полного использования линейной сети необходим новый компонент - линия задержки с отводом. Такая линия задержки показана ниже. Там входной сигнал поступает слева и проходит через N-1 задержки. Выходной сигнал линии задержки с отводом (TDL) представляет собой N-мерный вектор, состоящий из входного сигнала в текущий момент времени, предыдущего входного сигнала и т.д.

Линейный фильтр

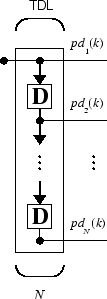
Для создания показанного линейного фильтра можно объединить линию задержки с линейной сетью.

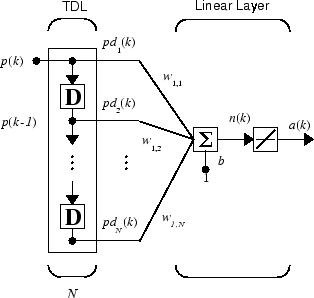
Выход фильтра задается

$α (k) = пурелин (Wp_{+ b}^{)}_{} =\sumi=1Rw1,ip ($ k − i + 1) + b

Показанная сеть упоминается в поле обработки цифрового сигнала как фильтр с конечной импульсной характеристикой (FIR) [WiSt85]. Посмотрите на код, используемый для создания и моделирования такой сети.

Предположим, что требуется линейный слой, выводящий последовательность T, учитывая последовательность P и два начальных состояния задержки на входе Pi.

P = {1 2 1 3 3 2};
Pi = {1 3};
T = {5 6 4 20 7 8};

Вы можете использовать newlind создание сети с задержками для получения соответствующих выходных данных для входных данных. Начальные выходные сигналы задержки подаются в качестве третьего аргумента, как показано ниже.

net = newlind(P,T,Pi);

Выходные данные проектируемой сети можно получить с помощью

Y = net(P,Pi)

дать

Y = [2.7297] [10.5405] [5.0090] [14.9550] [10.7838] [5.9820]

Как видно, сетевые выходы не совсем равны целевым, но они близки и среднеквадратическая ошибка минимизируется.

Алгоритм LMS (learnwh)

Алгоритм LMS, или алгоритм обучения Widrow-Hoff, основан на приблизительной процедуре наиболее крутого спуска. Здесь снова линейные сети обучаются на примерах правильного поведения.

Widrow и Hoff имели представление, что они могут оценить среднеквадратическую ошибку, используя квадрат ошибки в каждой итерации. Если взять частную производную квадратичной ошибки относительно весов и смещений в k-ой итерации, то

$\frac{^{∂e2} (k}{)_{}} ∂w1,j=2e \frac{(k)}{\partiale_{(k)}}$ ∂w1,j

для j = 1,2,...,R и

$\frac{^{∂e2} (k}{)} ∂b=2e \frac{(k)}{\partiale}$ (k) ∂b

Далее рассмотрим частную производную относительно ошибки.

$\frac{∂e (k}{)_{}} \frac{∂w1,j=∂[t (k) -}{α_{(k)}}] \frac{}{_{}} ∂w1,j=∂∂w1,j[t (k) -$ (Wp (k) + b)]

или

$\frac{∂e (k}{)_{}} \frac{}{_{}} ∂w1,j=∂∂w1,j[t (k)_{-}^{(}_{}_{} ∑i=1Rw1,ipi ($ k) + b)]

Здесь _pi (k) - i-й элемент входного вектора на k-ой итерации.

Это можно упростить до

$\frac{∂e (k}{)_{}}_{} ∂w1,j=−pj$ (k)

$\frac{∂e (k}{)}$ ∂b=−1

Наконец, измените матрицу веса, и смещение будет

2αe (k) p (k)

2αe (k)

Эти два уравнения составляют основу алгоритма обучения Widrow-Hoff (LMS).

Эти результаты могут быть распространены на случай множественных нейронов и записаны в матричной форме как

$\begin{array}{l} W (k + 1) = W (k) +^{} 2αe \\ (k) pT (k) b (k + \end{array}$ 1) = b (k) + 2αe (k)

Здесь ошибка e и смещение b являются векторами, а α является скоростью обучения. Если α велик, обучение происходит быстро, но если он слишком велик, это может привести к нестабильности, и ошибки могут даже увеличиться. Для обеспечения стабильного обучения скорость обучения должна быть меньше, чем обратная величина наибольшего собственного значения корреляционной матрицы pTp входных векторов.

Для получения дополнительной информации об алгоритме LMS и его сходимости можно ознакомиться с главой 10 [HDB96].

К счастью, есть функция инструментария, learnwh, это делает все расчеты для вас. Он вычисляет изменение веса как

dw = lr*e*p'

и изменение смещения как

db = lr*e

Константа 2, показанная несколькими строками выше, была поглощена скоростью обучения коду. lr. Функция maxlinlr вычисляет эту максимальную стабильную скорость обучения lr как 0,999 * P'*P.

Напечатать help learnwh и help maxlinlr для получения более подробной информации об этих двух функциях.

Линейная классификация (поезд)

Линейные сети могут быть обучены выполнению линейной классификации с помощью функции train. Эта функция применяет каждый вектор набора входных векторов и вычисляет приращения веса сети и смещения из-за каждого из входов в соответствии с learnp. Затем сеть корректируется с учетом суммы всех этих поправок. Каждый проход через входные векторы называется эпохой. Это контрастирует с adapt который регулирует веса для каждого входного вектора в том виде, в каком он представлен.

Наконец, train применяет входные данные к новой сети, вычисляет выходные данные, сравнивает их с соответствующими целевыми значениями и вычисляет среднеквадратическую ошибку. Если цель ошибки достигнута или достигнуто максимальное количество периодов, обучение прекращается, и train возвращает новую сеть и запись обучения. Иначе train переживает другую эпоху. К счастью, алгоритм LMS сходится при выполнении этой процедуры.

Простая проблема иллюстрирует эту процедуру. Рассмотрим линейную сеть, представленную ранее.

Предположим, что существует следующая проблема классификации.

${_{p1} = \begin{array}{l} \end{array} [22],_{} t1=0} {_{p2} = \begin{matrix} \end{matrix} [1-2],_{} t2=1} {_{p3} = \begin{matrix} [−22 \end{matrix}],_{} t3=0} {_{p4} = \begin{matrix} [−11 \end{matrix}],_{} t4=1}$

Здесь есть четыре входных вектора, и вы хотите сеть, которая производит выход, соответствующий каждому входному вектору, когда этот вектор представлен.

Использовать train получение весов и смещений для сети, которая производит правильные цели для каждого входного вектора. По умолчанию начальные веса и смещение для новой сети равны 0. Установите для цели ошибки значение 0,1, а не принимайте значение по умолчанию 0.

P = [2 1 -2 -1;2 -2 2 1];
T = [0 1 0 1];
net = linearlayer;
net.trainParam.goal= 0.1;
net = train(net,P,T);

Задача выполняется для 64 эпох, достигая среднеквадратической ошибки 0,0999. Новые веса и смещение

weights = net.iw{1,1}
weights =
   -0.0615   -0.2194
bias = net.b(1)
bias =
    [0.5899]

Можно смоделировать новый сетевой график, как показано ниже.

A = net(P)
A =
    0.0282    0.9672    0.2741    0.4320

Можно также вычислить ошибку.

err = T - sim(net,P)
err =
   -0.0282    0.0328   -0.2741    0.5680

Обратите внимание, что цели не реализованы точно. Проблема работала бы дольше в попытке получить идеальные результаты, если бы была выбрана меньшая цель ошибки, но в этой проблеме невозможно получить цель 0. Сеть ограничена по своим возможностям. Примеры различных ограничений см. в разделе Ограничения и предостережения.

Эта примерная программа, Training a Linear Neuron, показывает тренировку линейного нейрона и строит график траектории веса и ошибки во время тренировки.

Также можно попробовать запустить программу-пример nnd10lc. В нем рассматривается классическая и исторически интересная проблема, показано, как сеть можно обучить классификации различных шаблонов, и показано, как обучаемая сеть реагирует на появление шумных шаблонов.

Ограничения и предостережения

Линейные сети могут изучать только линейные отношения между входным и выходным векторами. Таким образом, они не могут найти решения некоторых проблем. Однако, даже если идеального решения не существует, линейная сеть минимизирует сумму квадратичных ошибок, если скорость обучения lr достаточно мал. Сеть найдет как можно более близкое решение, учитывая линейный характер архитектуры сети. Это свойство сохраняется, поскольку поверхность ошибки линейной сети является многомерной параболой. Поскольку параболы имеют только один минимум, алгоритм градиентного спуска (такой как правило LMS) должен дать решение на этом минимуме.

Линейные сети имеют различные другие ограничения. Некоторые из них обсуждаются ниже.

Сверхопределённые системы

Рассмотрим сверхопределённую систему. Предположим, что у вас есть сеть для обучения с четырьмя одноэлементными входными векторами и четырьмя целевыми объектами. Идеального решения wp + b = t для каждого из входов может не быть, поскольку существует четыре ограничивающих уравнения, и только один вес и одно смещение для регулировки. Однако правило LMS по-прежнему минимизирует ошибку. Чтобы увидеть, как это делается, можно попробовать команду «Линейная посадка нелинейной проблемы».

Недостаточно определенные системы

Рассмотрим один линейный нейрон с одним входом. На этот раз в Underdefined Problem обучите его только одному одноэлементному входному вектору и его одноэлементному целевому вектору:

P = [1.0];
T = [0.5];

Заметим, что хотя существует только одно ограничение, возникающее из одной пары вход/цель, есть две переменные, вес и смещение. Наличие большего количества переменных, чем ограничений, приводит к неопределенной проблеме с бесконечным числом решений. Чтобы ознакомиться с этой темой, можно попробовать определить неполадку.

Линейно-зависимые векторы

Обычно это простая задача определить, может ли линейная сеть решить проблему. Обычно, если линейная сеть имеет по меньшей мере столько же степеней свободы (S * R + S = число весов и смещений), сколько ограничения (Q = пары входных/целевых векторов), то сеть может решить проблему. Это верно, за исключением случаев, когда входные векторы линейно зависимы и применяются к сети без смещений. В этом случае, как показано в примере Linearly Dependent Problem, сеть не может решить проблему с нулевой ошибкой. Вы можете попробовать линейно зависимую проблему.

Слишком большая скорость обучения

Линейную сеть всегда можно обучить с помощью правила Widrow-Hoff, чтобы найти минимальное решение ошибки для ее весов и отклонений, если скорость обучения достаточно мала. Пример Слишком большая скорость обучения показывает, что происходит, когда нейрон с одним входом и смещением обучается с частотой обучения больше, чем рекомендуется maxlinlr. Сеть обучается с двумя различными скоростями обучения, чтобы показать результаты использования слишком большой скорости обучения.

Документация