Фундаментальным строительным блоком для нейронных сетей является нейрон с одним входом, такой как этот пример.
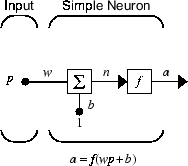
Есть три различные функциональные операции, которые происходят в этом примере нейрона. Сначала скалярный вход p умножается на скалярный вес w, чтобы сформировать произведение wp, снова скаляр. Во-вторых, взвешенный вход wp добавляется к скалярному смещению b, чтобы сформировать чистый вход n. (В этом случае можно рассматривать смещение как смещение функции f влево на величину b. Смещение во многом похоже на вес, за исключением того, что оно имеет постоянный вход 1.) Наконец, чистый вход проходит через передаточную функцию f, которая производит скалярный выход a. Имена этих трех процессов: весовая функция, чистая входная функция и передаточная функция.
Для многих типов нейронных сетей весовая функция является произведением веса, умноженного на вход, но иногда используются другие весовые функции (например, расстояние между весом и входом, | w − p |). (Для получения списка весовых функций введитеhelp nnweight.) Наиболее распространенной функцией полного ввода является суммирование взвешенных входных данных со смещением, но могут использоваться другие операции, такие как умножение. (Для получения списка функций сетевого ввода введите help nnnetinput.) Введение в радиальные базовые нейронные сети (Radial Basis Neural Networks) обсуждает, как расстояние может использоваться в качестве весовой функции, а умножение может использоваться в качестве сетевой входной функции. Существует также множество типов функций переноса. Примеры различных функций переноса приведены в разделе Функции переноса. (Для получения списка функций переноса введите help nntransfer.)
Обратите внимание, что w и b являются регулируемыми скалярными параметрами нейрона. Центральная идея нейронных сетей заключается в том, что такие параметры могут быть отрегулированы так, чтобы сеть проявляла некоторое желаемое или интересное поведение. Таким образом, можно обучить сеть выполнению определенной задачи путем корректировки параметров веса или смещения.
Все нейроны в программном обеспечении Deep Learning Toolbox™ имеют обеспечение смещения, и смещение используется во многих примерах и предполагается в большинстве из этого инструментария. Тем не менее, вы можете пропустить смещение в нейроне, если хотите.
Многие функции передачи включены в программное обеспечение Deep Learning Toolbox.
Ниже приведены две наиболее часто используемые функции.
На следующем рисунке показана линейная передаточная функция.
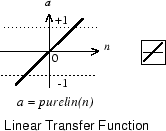
Нейроны этого типа используются в конечном слое многослойных сетей, которые используются в качестве аппроксиматоров функций. Это показано в многоуровневых неглубоких нейронных сетях и обучении обратному распространению.
Сигмоидальная передаточная функция, показанная ниже, принимает входной сигнал, который может иметь любое значение между плюс и минус бесконечностью, и сжимает выходной сигнал в диапазоне от 0 до 1.
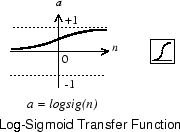
Эта передаточная функция обычно используется в скрытых слоях многослойных сетей, отчасти потому, что она дифференцируется.
Символ в квадрате справа от каждого графика передаточной функции, показанного выше, представляет ассоциированную передаточную функцию. Эти значки заменяют общие f в блоках схемы сети для отображения конкретной используемой функции передачи.
Для получения полного списка функций переноса введите help nntransfer. Можно также указать собственные функции переноса.
Вы можете поэкспериментировать с простым нейроном и различными передаточными функциями, запустив примерную программу nnd2n1.
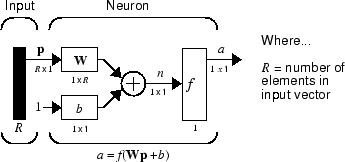
Простой нейрон может быть расширен для обработки входов, которые являются векторами. Нейрон с одним R-элементом входного вектора показан ниже. Здесь отдельные элементы ввода
p1,p2,...pR
умножаются на веса
w1,1,w1,2,...w1,R
и взвешенные значения подаются на суммирующий переход. Их сумма - это просто Wp, скалярное произведение (одиночной строки) матрицы W и вектора p. (Есть и другие весовые функции, помимо скалярного произведения, такие как расстояние между строкой весовой матрицы и входным вектором, как во введении к радиальным базовым нейронным сетям.)
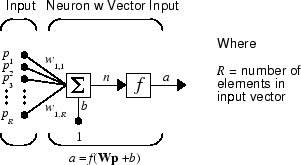
Нейрон имеет смещение b, которое суммируется со взвешенными входами, чтобы сформировать чистый вход n. (В дополнение к суммированию, могут использоваться другие сетевые входные функции, такие как умножение, которое используется во введении к радиальным базовым нейронным сетям.) Чистый вход n является аргументом передаточной функции f.
w1, RpR + b
Это выражение, конечно, можно записать в коде MATLAB ® как
n = W*p + b
Однако вы редко будете писать код на этом уровне, поскольку такой код уже встроен в функции для определения и моделирования целых сетей.
Фигура одного нейрона, показанная выше, содержит много деталей. Когда вы рассматриваете сети со многими нейронами, и, возможно, слоями многих нейронов, есть столько деталей, что основные мысли, как правило, теряются. Таким образом, авторы разработали сокращенное обозначение для отдельного нейрона. Эта запись, которая используется позже в цепях нескольких нейронов, показана здесь.
Здесь входной вектор p представлен сплошной темной вертикальной полосой слева. Размеры p показаны под символом p на рисунке как R × 1. (Обратите внимание, что при ссылке на размер вектора используется заглавная буква, например R в предыдущем предложении.) Таким образом, p является вектором R входных элементов. Как и прежде, константа 1 входит в нейрон как вход и умножается на скалярное смещение b. Чистый вход в передаточную функцию f равен n, сумме смещения b и произведения Wp. Эта сумма передается в передаточную функцию f, чтобы получить выход нейрона a, который в данном случае является скаляром. Заметим, что если бы было больше одного нейрона, сетевой выход был бы вектором.
Уровень сети определен на предыдущем рисунке. Слой включает в себя весовые коэффициенты, операции умножения и суммирования (здесь реализуемые как векторное произведение Wp), смещение b и передаточную функцию f. Массив входных сигналов, вектор p, не включается в или называется слоем.
Как и в случае с Simple Neuron, в слое происходит три операции: весовая функция (умножение матрицы, или скалярное произведение, в данном случае), сетевая входная функция (суммирование, в данном случае) и передаточная функция.
Каждый раз, когда используется эта сокращенная сетевая нотация, размеры матриц отображаются чуть ниже их имен матричных переменных. Эта нотация позволит понять архитектуры и следовать матричной математике, связанной с ними.
Как описано в разделе Передаточные функции, когда конкретная передаточная функция должна использоваться на чертеже, символ для этой передаточной функции заменяет символ f, показанный выше. Вот несколько примеров.

Вы можете поэкспериментировать с двухэлементным нейроном, запустив примерную программу nnd2n2.