В этом разделе рассматривается влияние формата структур входных данных на моделирование сетей. Она начинается со статических сетей, а затем продолжается с динамических сетей. В следующем разделе описывается, как формат структур данных влияет на обучение сети.
Существует два основных типа входных векторов: те, которые происходят одновременно (одновременно, или не в конкретной временной последовательности), и те, которые происходят последовательно во времени. Для параллельных векторов порядок не важен, и если бы было несколько сетей, работающих параллельно, можно было бы представить один входной вектор каждой из сетей. Для последовательных векторов важен порядок появления векторов.
Простейшая ситуация для моделирования сети возникает, когда моделируемая сеть является статической (не имеет обратной связи или задержек). В этом случае не нужно беспокоиться о том, возникают ли входные векторы в определенной временной последовательности, поэтому можно рассматривать входные данные как параллельные. Кроме того, проблема становится еще проще, предполагая, что сеть имеет только один входной вектор. В качестве примера используйте следующую сеть.
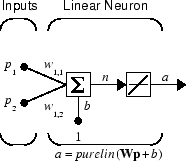
Чтобы настроить эту линейную сеть прямой связи, используйте следующие команды:
net = linearlayer;
net.inputs{1}.size = 2;
net.layers{1}.dimensions = 1;
Для простоты назначьте весовую матрицу и смещение W = [1 2] и b = [0].
Команды для этих назначений:
net.IW{1,1} = [1 2];
net.b{1} = 0;
Предположим, что набор данных моделирования сети состоит из Q = 4 параллельных векторов:
Параллельные векторы представлены сети в виде единой матрицы:
P = [1 2 2 3; 2 1 3 1];
Теперь можно смоделировать сетевой график:
A = net(P)
A =
5 4 8 5
Сеть представляет одну матрицу параллельных векторов, и сеть формирует одну матрицу параллельных векторов в качестве выходных данных. Результат будет одинаковым, если будут четыре сети, работающие параллельно, и каждая сеть примет один из входных векторов и произведет один из выходов. Упорядочение входных векторов не важно, поскольку они не взаимодействуют друг с другом.
Когда сеть содержит задержки, вход в сеть обычно представляет собой последовательность входных векторов, которые происходят в определенном временном порядке. Для иллюстрации этого случая на следующем рисунке показана простая сеть, содержащая одну задержку.
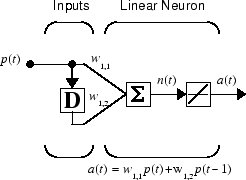
Эту сеть создают следующие команды:
net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
Назначьте весовую матрицу W = [1 2].
Команда:
net.IW{1,1} = [1 2];
Предположим, что входная последовательность:
Последовательные входы представлены в сеть как элементы массива ячеек:
P = {1 2 3 4};
Теперь можно смоделировать сетевой график:
A = net(P)
A =
[1] [4] [7] [10]
Вводится массив ячеек, содержащий последовательность входов, а сеть создает массив ячеек, содержащий последовательность выходов. Порядок входных данных важен, когда они представлены в виде последовательности. В этом случае выходной ток получается умножением входного тока на 1 и предыдущего входного сигнала на 2 и суммированием результата. При изменении порядка ввода номера, полученные на выходе, изменятся.
Если применить те же входные данные, что и набор параллельных входных данных вместо последовательности входных данных, будет получен совершенно другой ответ. (Однако непонятно, зачем это делать с динамической сетью.) Было бы так, как если бы каждый вход подавался одновременно в отдельную параллельную сеть. В предыдущем примере «Моделирование с последовательными входами в динамической сети» (Simulation with Sequential Inputs in a Dynamic Network), если используется параллельный набор вводов
который может быть создан со следующим кодом:
P = [1 2 3 4];
При моделировании с параллельными вводами получается
A = net(P)
A =
1 2 3 4
Результат такой же, как если бы вы одновременно применяли каждый из входов к отдельной сети и вычисляли один выход. Обратите внимание, что, поскольку вы не назначили задержкам сети какие-либо начальные условия, они предполагались равными 0. В этом случае выходной сигнал просто в 1 раз превышает входной сигнал, поскольку вес, умножающий текущий входной сигнал, равен 1.
В некоторых особых случаях может потребоваться имитация ответа сети на несколько различных последовательностей одновременно. В этом случае необходимо представить сеть с параллельным набором последовательностей. Например, предположим, что необходимо представить сети две следующие последовательности:
Вход P должен быть массивом ячеек, где каждый элемент массива содержит два элемента двух последовательностей, которые происходят одновременно:
P = {[1 4] [2 3] [3 2] [4 1]};
Теперь можно смоделировать сетевой график:
A = net(P);
Результирующий сетевой выход будет
A = {[1 4] [4 11] [7 8] [10 5]}
Как видно, первый столбец каждой матрицы составляет выходную последовательность, созданную первой входной последовательностью, которая использовалась в предыдущем примере. Второй столбец каждой матрицы составляет выходную последовательность, формируемую второй входной последовательностью. Взаимодействие между двумя параллельными последовательностями отсутствует. Как будто все они были применены к отдельным сетям, работающим параллельно.
На следующей диаграмме показан общий формат сетевого входа P при наличии Q параллельных последовательностей временных шагов TS. Он охватывает все случаи, когда существует один входной вектор. Каждый элемент массива ячеек является матрицей параллельных векторов, которые соответствуют одному и тому же моменту времени для каждой последовательности. Если имеется несколько входных векторов, в массиве ячеек будет множество строк матриц.
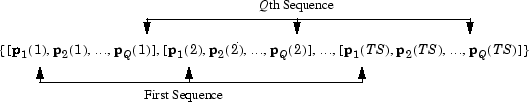
В этом разделе рассматривается применение последовательных и параллельных входных данных к динамическим сетям. При моделировании с параллельными входами в статической сети к статическим сетям применяются параллельные входы. Также можно применять последовательные входы к статическим сетям. Он не изменяет смоделированный отклик сети, но может повлиять на способ обучения сети. Это станет ясно из Концепции обучения нейронной сети.
См. также Настройка неглубоких входов и выходов нейронной сети.