Поворот кадра кватерниона
rotationResult = rotateframe(quat,cartesianPoints)quat. Элементы кватерниона нормализуются перед использованием при вращении.
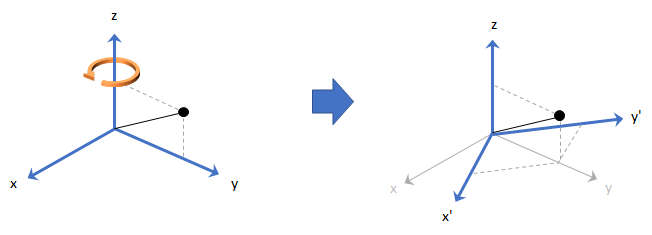
Поворот рамки кватерниона повторно ссылается на точку, указанную в R3, путем поворота исходной рамки отсчета в соответствии с указанным кватернионом:
* uq
где q - кватернион, * - сопряжение, а u - точка вращения, заданная как кватернион.
Для удобства, rotateframe функция принимает точку в R3 и возвращает точку в R3. Учитывая вызов функции с некоторым произвольным кватернионом, q = a + bi + cj + dk и произвольной координатой, [x, y, z ],
point = [x,y,z]; rereferencedPoint = rotateframe(q,point)
rotateframe выполняет следующие операции:
Преобразует точку [x, y, z] в кватернион:
yj + zk
Нормализует кватернион, q:
c2 + d2
Применяет поворот:
uqq
Преобразует выход кватерниона vq обратно в R3