dsp. HampelFilter

Фильтрация отклонений по идентификатору Hampel

Описание

dsp.HampelFilter Система object™ обнаруживает и удаляет отклонения входного сигнала с помощью идентификатора Хампеля. Идентификатор Хампеля - это разновидность правила статистики с тремя сигмами, которая надежна против отклонений. Для каждой выборки входного сигнала объект вычисляет медиану окна, составленного из текущей выборки и Len $\frac{−}{}$ 12 смежных выборок на каждой стороне текущей выборки. Len - длина окна, заданная через WindowLength собственность. Объект также оценивает стандартное отклонение каждого образца относительно его оконной медианы, используя медианное абсолютное отклонение. Если выборка отличается от медианы более чем на пороговое значение, умноженное на стандартное отклонение, фильтр заменяет выборку на медиану. Дополнительные сведения см. в разделе Алгоритмы.

Для фильтрации входного сигнала по идентификатору Хампеля:

Создать dsp.HampelFilter и задайте его свойства.
Вызовите объект с аргументами, как если бы это была функция.

Дополнительные сведения о работе системных объектов см. в разделе Что такое системные объекты?.

Создание

Синтаксис

hampFilt = dsp. HampelFilter

hampFilt = dsp. HampelFilter (Len)

hampFilt = dsp. HampelFilter (Лен, Лим)

hampFilt = dsp. HampelFilter (имя, значение)

Описание

hampFilt = dsp.HampelFilter возвращает объект фильтра Хампеля, hampFilt, используя свойства по умолчанию.

пример

hampFilt = dsp.HampelFilter(Len) устанавливает WindowLength свойство для Len.

hampFilt = dsp.HampelFilter(Len, Lim) устанавливает WindowLength свойство для Len и Threshold свойство для Lim.

Пример: hampFilt = dsp.HampelFilter(11,2);

hampFilt = dsp.HampelFilter(Name,Value) задает свойства с помощью Name,Value пар. Неопределенные свойства имеют значения по умолчанию.

Свойства

развернуть все

Если не указано иное, свойства не настраиваются, что означает невозможность изменения их значений после вызова объекта. Объекты блокируются при их вызове, и release функция разблокирует их.

Если свойство настраивается, его значение можно изменить в любое время.

Дополнительные сведения об изменении значений свойств см. в разделе Проектирование системы в MATLAB с использованием системных объектов.

Если свойство указано как настраиваемое, его значение можно изменить, даже если объект заблокирован.

`WindowLength` - Длина скользящего окна
`11` (по умолчанию) | положительное нечетное скалярное целое

Длина скользящего окна, заданная как положительное нечетное скалярное целое число. Окно конечной длины скользит по данным, и объект вычисляет среднее и среднее абсолютное отклонение данных в окне.

Типы данных: single | double

`Threshold` - Пороговое значение для обнаружения отклонений
3 (по умолчанию) | положительный вещественный скаляр

Порог обнаружения отклонений, заданный как положительный действительный скаляр. Сведения о том, как это свойство используется для обнаружения отклонений, см. в разделе Алгоритмы.

Настраиваемый: Да

Типы данных: single | double

Использование

Синтаксис

y = hampFilt (x)

[y, isOutlier] = hampFilt (x)

Описание

пример

y = hampFilt(x) обнаруживает и удаляет отклонения каждого канала входного сигнала, xнезависимо с течением времени с использованием фильтра Хампеля.

[y,isOutlier] = hampFilt(x) возвращает логический массив, isOutlier, в котором каждый true элемент указывает, что соответствующий элемент на входе является отклонением. isOutlier имеет тот же размер, что и входной и выходной векторы.

Входные аргументы

развернуть все

`x` - Ввод данных
вектор | матрица

Ввод данных, заданный как вектор или матрица. Объект принимает многоканальные входы, то есть входы размера m на n, где m ≥ 1, и n > 1. m - число выборок в каждом кадре (канале), а n - число каналов. Объект также принимает входные данные переменного размера. После блокировки объекта можно изменить размер каждого входного канала, но нельзя изменить количество каналов.

Типы данных: single | double

Выходные аргументы

развернуть все

`y` - Отфильтрованные данные
вектор | матрица

Отфильтрованные данные, возвращенные в виде вектора или матрицы.

Типы данных: single | double

`isOutlier` - Указать отклонение
`true` | `false`

Логический массив, элементы которого указывают, является ли соответствующий элемент во входном массиве отклонением. Если элемент в isOutlier является true, соответствующий элемент во входном массиве является отклонением.

Типы данных: logical

Функции объекта

Чтобы использовать функцию объекта, укажите объект System в качестве первого входного аргумента. Например, для освобождения системных ресурсов объекта System с именем obj, используйте следующий синтаксис:

release(obj)

развернуть все

Общие для всех системных объектов

`step`	Запустить алгоритм объекта System
`release`	Деблокирование ресурсов и разрешение изменений значений свойств объекта системы и входных признаков
`reset`	Сброс внутренних состояний объекта System

Примеры

свернуть все

Удаление высокочастотного шума с помощью фильтра Хэмпела

Открыть сценарий

Фильтрация высокочастотного шума от шумового синусоидального сигнала с помощью фильтра Хампеля. Сравните производительность фильтра Хампеля с фильтром медианы.

Инициализация

Настройка dsp.HampelFilter и dsp.MedianFilter объект. Эти объекты используют метод скользящего окна с длиной окна 7. Создайте область времени для просмотра выходных данных.

Fs = 1000;
hampFilt = dsp.HampelFilter(7);
medFilt = dsp.MedianFilter(7);
scope  = timescope('SampleRate',Fs, ...
    'TimeSpanOverrunAction','Scroll', ...
    'TimeSpanSource','Property',...
    'TimeSpan',1,'ShowGrid',true, ...
    'LayoutDimensions',[3 1], ...
    'NumInputPorts',3);
scope.ActiveDisplay = 1;
scope.Title = 'Signal + Noise';
scope.YLimits = [-1 3];
scope.ActiveDisplay = 2;
scope.Title = 'Hampel Filter Output (Window Length = 7)';
scope.YLimits = [-1 1];
scope.ActiveDisplay = 3;
scope.Title = 'Median Filter Output (Window Length = 7)';
scope.YLimits = [-1 1];

Фильтрация шумной синусоидальной волны с помощью окна длиной 7

Генерация шумного синусоидального сигнала с частотой 10 Гц. Примените к сигналу фильтр Хампеля и объект медианного фильтра. Просмотрите выходные данные области времени.

FrameLength = 256;
sine = dsp.SineWave('SampleRate',Fs,'Frequency',10,...
    'SamplesPerFrame',FrameLength);

for i = 1:500
    hfn = 3 * (rand(FrameLength,1) < 0.02);
    x = sine() + 1e-2 * randn(FrameLength,1) + hfn;
    y1 = hampFilt(x);
    y2 = medFilt(x);
    scope(x,y1,y2);
end
release(scope)

Оба фильтра снимают высокочастотный шум. Однако при увеличении длины окна предпочтителен фильтр Хампеля. В отличие от медианного фильтра, фильтр Хампеля сохраняет форму синусоидальной волны даже при больших длинах окон.

Фильтрация шумной синусоидальной волны с помощью окна длиной 37

Увеличьте длину окна обоих фильтров до 37. Фильтрация шумной синусоидальной волны и просмотр отфильтрованных выходных данных во временной области. Чтобы изменить длину окна фильтров, необходимо освободить объекты фильтра в начале цикла обработки.

release(hampFilt);
release(medFilt);
hampFilt.WindowLength = 37;
medFilt.WindowLength = 37;
scope.ActiveDisplay = 1;
scope.Title = 'Signal + Noise';
scope.ActiveDisplay = 2;
scope.Title = 'Hampel Filter Output (Window Length = 37)';
scope.ActiveDisplay = 3;
scope.Title = 'Median Filter Output (Window Length = 37)';
for i = 1:500
    hfn = 3 * (rand(FrameLength,1) < 0.02);
    x = sine() + 1e-2 * randn(FrameLength,1) + hfn;
    y1 = hampFilt(x);
    y2 = medFilt(x);
    scope(x,y1,y2);
end
release(scope)

Медианный фильтр выравнивает гребни и впадины синусоидальной волны из-за медианной операции над большим окном данных. Фильтр Хампеля сохраняет форму сигнала в дополнение к удалению отклонений.

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпела

Открыть сценарий

Удалите высокочастотные отклонения из потокового сигнала с помощью dsp.HampelFilter object™ системы.

Используйте dsp.MatFileReader Системный объект для чтения файла MAT гироскопа. Файл содержит три столбца данных, каждый из которых содержит 7140 образцов. Три столбца представляют данные оси X, оси Y и оси Z от датчика движения гироскопа. Выберите размер кадра 714 выборок так, чтобы каждый столбец данных содержал 10 кадров. dsp.HampelFilter Системный объект использует длину окна 11. Создать timescope для просмотра отфильтрованных выходных данных.

reader = dsp.MatFileReader('SamplesPerFrame',714,'Filename','LSM9DSHampelgyroData73.mat', ...
    'VariableName','data');
hampFilt = dsp.HampelFilter(11);
scope = timescope('NumInputPorts',1,'SampleRate',119,'YLimits',[-300 300], ...
    'ChannelNames',{'Input','Filtered Output'},...
    'TimeSpanSource','Property','TimeSpan',60,'ShowLegend',true);

Фильтрация данных гироскопа с помощью dsp.HampelFilter Системный объект. Просмотрите отфильтрованные данные по оси Z во временной области.

for i = 1:10
    gyroData = reader();
    filteredData = hampFilt(gyroData);
    scope([gyroData(:,3),filteredData(:,3)]);
end

Фильтр Хампеля удаляет все отклонения и сохраняет форму сигнала.

Подробнее

развернуть все

Идентификатор Хампеля

Идентификатор Хампеля - это разновидность правила статистики с тремя сигмами, которая надежна против отклонений.

Учитывая последовательность x1, x2, x3, ... , _xn и скользящее окно длиной k, определите медиану точка-точка и оценки стандартного отклонения, используя:

Локальная медиана - $_{mi} = {медиана}_{(} xi_{- k,} {xi}_{- k} + 1,_{} xi -_{k +} 2,_{. . .,} {xi}_{, . .} .$ , xi + k − 2, xi + k − 1, xi + k)
Среднеквадратическое отклонение - $_{starti} = αmedian_{(|} {xi}_{} - k -_{mi} |,_{.} . .,$ | xi + $k \frac{}{\sqrt{−} {mi}^{|)},} где start= =$ 12erfc − 1 (1/2) ≈1.4826

Величина _{starti/startизвестна} известна как среднее абсолютное отклонение (MAD).

Если образец _xi таков, что

$|_{} xi_{-} {mi}_{} |_{}$ > n

для данного порога _nstart, то идентификатор Хампеля объявляет _xi отклонением и заменяет его _{на mi}. Если _nλ равно 0, то фильтр Хампеля ведёт себя как обычный медианный фильтр.

Алгоритмы

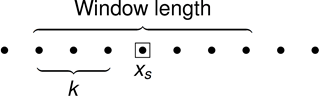
Для данной выборки данных xs алгоритм:

Центрирует окно нечетной длины по текущему образцу.
Вычисляет локальное медианное значение, _mi и стандартное отклонение _по текущему окну данных.
Сравнивает текущую выборку с _n Если $|_{} xs_{-} {mi}_{} |_{>}$ nstart× × i, фильтр идентифицирует текущий _{образец}, xs, как выброс и заменяет его медианным _{значением}, mi.

Рассмотрим кадр данных, который передается в фильтр Хампеля.

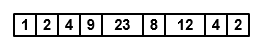
В этом примере фильтр Хампеля перемещает окно длиной 5 (Len) по данным. Фильтр имеет пороговое значение 2 (_nλ). Чтобы иметь полное окно в начале кадра, алгоритм фильтра дополняет кадр нулями Len - 1. Для вычисления первой выборки выходного сигнала окно центрируется на ${[\frac{Len −}{} 12}^{+}$ 1] -й выборке в добавленном кадре, третий ноль в данном случае. Фильтр вычисляет медиану, среднее абсолютное отклонение и стандартное отклонение по данным в локальном окне.

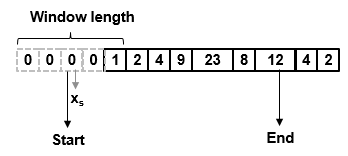
Текущая выборка: _xs = 0.
Окно данных: win = [0 0 0 0 1].
Локальная медиана: _mi = медиана ([0 0 0 0 1]) = 0.
Медианное абсолютное отклонение: $_{мади} = медиана_{(|} {xi}_{} - k -_{mi} |,_{.} . .$ , | xi + k − mi |). Для $этого окна данных mad =$ медиана (| 0 − 0 |,..., | 1 − 0 |) = 0.
Среднеквадратическое отклонение: _starti = start× _madi = 0, где $start= \frac{=}{\sqrt{}^{12erfc} − 1} (1/2)$ ≈1.4826.
Текущая выборка, _xs = 0, не подчиняется отношению для обнаружения отклонений.

$[|_{} xs_{-} mi | =_{0}]_{>} [($ n
Поэтому фильтр Хампеля выводит текущую входную выборку, _xs = 0.

Повторите эту процедуру для каждого последующего образца, пока алгоритм не центрирует окно на ${[End \frac{- Len}{} -}^{}$ 12] -м образце, помеченном какEnd. Поскольку окно с центром на последних $\frac{}{}$ выборках Лен − 12 не может быть заполнено, эти выборки обрабатываются следующим кадром входных данных.

Вот первый выходной кадр, который генерирует фильтр Хампеля:

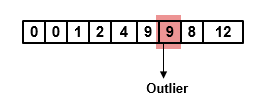
Седьмая выборка добавленного входного кадра 23 является отклонением. Фильтр Хампеля заменяет этот образец медианой над локальным окном [4 9 23 8 12].

Ссылки

[1] Боденем, Дин. «Адаптивная фильтрация и обнаружение изменений потоковых данных». PH.D. Дипломная работа. Имперский колледж, Лондон, 2012 год.

[2] Лю, Ханьчун, Сириш Шах и Вэй Цзян. «Обнаружение и очистка данных в режиме реального времени». Компьютеры и химическая инженерия. т. 28, март 2004, с. 1635-1647.

[3] Суомела, Юкка. Фильтрация медианы эквивалентна сортировке, 2014.

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™

Примечания и ограничения по использованию:

См. Системные объекты в создании кода MATLAB (кодер MATLAB).

См. также

Представлен в R2017a

Документация

dsp. HampelFilter

Описание

Создание

Синтаксис

Описание

Свойства

`WindowLength` - Длина скользящего окна
`11` (по умолчанию) | положительное нечетное скалярное целое

`Threshold` - Пороговое значение для обнаружения отклонений
3 (по умолчанию) | положительный вещественный скаляр

Использование

Синтаксис

Описание

Входные аргументы

`x` - Ввод данных
вектор | матрица

Выходные аргументы

`y` - Отфильтрованные данные
вектор | матрица

`isOutlier` - Указать отклонение
`true` | `false`

Функции объекта

Общие для всех системных объектов

Примеры

Удаление высокочастотного шума с помощью фильтра Хэмпела

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпела

Подробнее

Идентификатор Хампеля

Алгоритмы

Ссылки

Расширенные возможности

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™

См. также

Функции

Объекты

Блоки

Документация по системной панели инструментов DSP

Поддержка

Документация

dsp. HampelFilter

Описание

Создание

Синтаксис

Описание

Свойства

WindowLength - Длина скользящего окна 11 (по умолчанию) | положительное нечетное скалярное целое

Threshold - Пороговое значение для обнаружения отклонений 3 (по умолчанию) | положительный вещественный скаляр

Использование

Синтаксис

Описание

Входные аргументы

x - Ввод данных вектор | матрица

Выходные аргументы

y - Отфильтрованные данные вектор | матрица

isOutlier - Указать отклонение true | false

Функции объекта

Общие для всех системных объектов

Примеры

Удаление высокочастотного шума с помощью фильтра Хэмпела

Удаление высокочастотного шума из данных гироскопа с помощью фильтра Хэмпела

Подробнее

Идентификатор Хампеля

Алгоритмы

Ссылки

Расширенные возможности

Создание кода C/C + + Создайте код C и C++ с помощью MATLAB ® Coder™

См. также

Функции

Объекты

Блоки

Документация по системной панели инструментов DSP

Поддержка

`WindowLength` - Длина скользящего окна
`11` (по умолчанию) | положительное нечетное скалярное целое

`Threshold` - Пороговое значение для обнаружения отклонений
3 (по умолчанию) | положительный вещественный скаляр

`x` - Ввод данных
вектор | матрица

`y` - Отфильтрованные данные
вектор | матрица

`isOutlier` - Указать отклонение
`true` | `false`

Создание кода C/C + +
Создайте код C и C++ с помощью MATLAB ® Coder™