Для многих автономных систем знание состояния системы является необходимым условием для разработки любых приложений. На самом деле, однако, государство часто не является напрямую доступным. Состояние системы обычно вычисляется или оценивается на основе выходных сигналов системы, измеренных определенными приборами (такими как датчики), и потока состояния, управляемого динамической моделью или моделью движения. Некоторые простые методы, такие как оценка наименьших квадратов или пакетная оценка, достаточны для решения статических или автономных задач оценки. Для задач оценки в режиме онлайн и в реальном времени (последовательном) обычно применяются более сложные фильтры оценки.
Система оценки состоит из динамической модели или модели движения, которая описывает поток состояния, и модели измерения, которая описывает, как получаются измерения. Математически эти две модели могут быть представлены уравнением движения и уравнением измерения. Например, уравнение движения и уравнение измерения для общей нелинейной дискретной системы оценки может быть записано как:
h (xk)
где k - шаг времени, xk - состояние системы на шаге времени k, f (xk) - уравнение движения, зависящее от состояния, h (xk) - уравнение измерения, зависящее от состояния, и yk - выходной сигнал.
В большинстве случаев построение идеальной модели для отражения всего динамического явления невозможно. Например, включение всех трений в модель движения автономного транспортного средства невозможно. Чтобы компенсировать эту немодулированную динамику, в динамическую модель часто добавляют шум (w) процесса. Кроме того, при проведении измерений в измерения неизбежно включаются многочисленные источники ошибок, такие как ошибки калибровки. Чтобы учесть эти ошибки, в модель измерения необходимо добавить соответствующий шум измерения. Система оценки, включающая в себя эти случайные шумы и ошибки, называется стохастической системой оценки, которая может быть представлена следующим образом:
(xk, vk)
где wk и vk представляют технологический шум и измерительный шум соответственно.
Для большинства технических применений предполагается, что шум процесса и шум измерения следуют нулевому среднему гауссову или нормальному распределению или, по крайней мере, аппроксимируются гауссовым распределением. Также, поскольку точное состояние неизвестно, оценка состояния является случайной величиной, обычно предполагаемой для следования гауссовым распределениям. Предполагая, что гауссовы распределения для этих переменных значительно упрощают конструкцию оценочного фильтра, и составляют основу семейства фильтров Калмана.
Гауссово распределение для случайной величины (x) параметризуется средним значением λ и ковариационной матрицей P, которая записывается как x∼N (λ, P). Учитывая гауссово распределение, среднее, которое также является наиболее вероятным значением x, определяется ожиданием (E) как:
[x]
Среднее также называется первым моментом x о происхождении. Ковариация, описывающая неопределённость x, определяется ожиданием (E) как:
Ковариацию также называют вторым моментом x о её среднем значении.
Если размерность x равна единице, P является только скаляром. В этом случае значение P обычно обозначается, в свою очередь, δ 2 и называется дисперсией. Квадратный корень, λ, называется стандартным отклонением x. Стандартное отклонение имеет важное физическое значение. Например, на следующем рисунке показана функция плотности вероятности (которая описывает вероятность того, что х принимает определенное значение) для одномерного гауссова распределения со средним значением, равным λ, и стандартным отклонением, равным λ. Около 68% данных попадают в пределах границы 1λ x, 95% данных попадают в пределы границы 2, а 99,7% данных попадают в пределы границы 3λ.
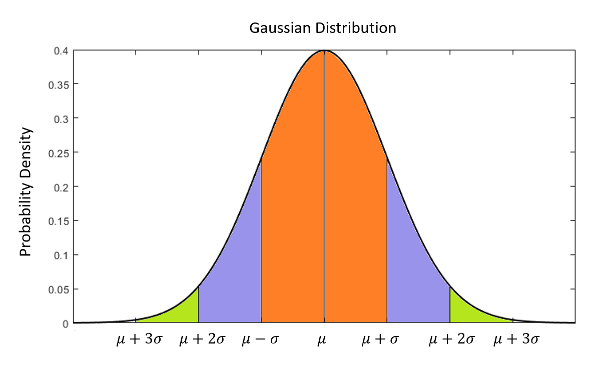
Хотя предположение о гауссовом распределении является доминирующим предположением в инженерных приложениях, существуют системы, состояние которых не может быть аппроксимировано гауссовыми распределениями. В этом случае для точной оценки состояния системы требуются некалмановские фильтры (например, фильтр частиц).
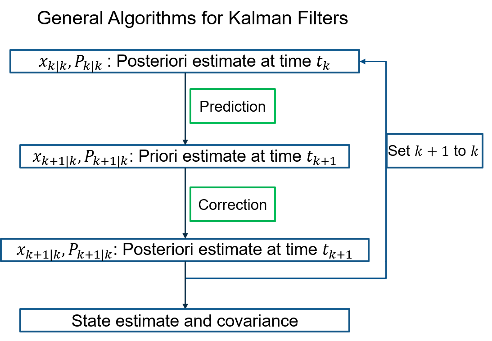
Целью проектирования фильтра является оценка состояния системы с использованием измерений и динамики системы. Поскольку измерения обычно проводятся на отдельных временных этапах, процесс фильтрации обычно разделяется на два этапа:
Прогнозирование: распространение состояния и ковариации между дискретными временными шагами измерения (k = 1, 2, 3,..., N) с использованием динамических моделей. Этот шаг также называется обновлением потока.
Коррекция: Коррекция оценки состояния и ковариации на дискретных временных этапах с использованием измерений. Этот шаг также называется обновлением измерений.
Для представления оценки состояния и состояния ковариации в различных шагах xk 'k и Pk' k обозначают оценку состояния и ковариацию после коррекции на временном шаге k, тогда как xk + 1 | k и Pk + 1 | k обозначают оценку состояния и ковариацию, предсказанную от предыдущего временного шага k до текущего временного шага k + 1.
На этапе прогнозирования распространение состояния является простым. Фильтр должен только подставлять оценку состояния в динамическую модель и распространять ее вперед во времени как xk + 1 | k = f (xk 'k).
Ковариационное распространение сложнее. Если система оценки является линейной, то ковариация может распространяться (Pk'k→Pk+1|k) точно в стандартном уравнении, основанном на свойствах системы. Для нелинейных систем точное распространение ковариации является сложной задачей. Основное различие между различными фильтрами заключается в том, как они распространяют ковариацию системы. Например:
Линейный фильтр Калмана использует линейное уравнение для точного распространения ковариации.
Расширенный фильтр Калмана распространяет ковариацию на основе линейной аппроксимации, что приводит к большим ошибкам, когда система является очень нелинейной.
Некачественный фильтр Калмана использует некачественное преобразование для выборки ковариационного распределения и его распространения во времени.
То, как распространяется состояние и ковариация, также сильно влияет на сложность вычисления фильтра. Например:
Линейный фильтр Калмана использует линейное уравнение для точного распространения ковариации, что обычно является вычислительно эффективным.
Расширенный фильтр Калмана использует линейные приближения, которые требуют вычисления якобиановых матриц и требуют больше вычислительных ресурсов.
Незаметный фильтр Калмана должен производить выборку ковариационного распределения и, следовательно, требует распространения множества точек выборки, что дорого для высокоразмерных систем.
На этапе коррекции фильтр использует измерения для коррекции оценки состояния посредством обратной связи измерения. В основном, разность между истинным измерением и предсказанным измерением добавляется к оценке состояния после того, как она умножается на матрицу усиления обратной связи. Например, в расширенном фильтре Калмана коррекция для оценки состояния задается следующим образом:
yk + 1 − h (xk + 1 | k))
Как уже упоминалось, xk + 1 | k - оценка состояния до (priori) коррекции, а xk + 1 | k + 1 - оценка состояния после (posteriori) коррекции. Kk - коэффициент усиления Калмана, определяемый оптимальным критерием, yk - истинное измерение, и h (xk + 1 | k) - прогнозируемое измерение.
На этапе коррекции фильтр также корректирует ковариацию ошибки оценки. Основная идея состоит в коррекции вероятностного распределения x с помощью информации о распределении yk + 1. Это называется апостериорной плотностью вероятности x, заданной y. В фильтре этапы прогнозирования и коррекции обрабатываются рекурсивно. Блок-схема показывает общие алгоритмы для фильтров Калмана.
Sensor Fusion and Tracking Toolbox™ предлагает несколько фильтров оценки, которые можно использовать для оценки и отслеживания состояния динамической системы.
Классический фильтр Кальмана (trackingKF) является оптимальным фильтром для линейных систем с гауссовым процессом и помехами измерений. Система линейной оценки может быть представлена следующим образом:
Hkxk + vk
Как технологический, так и измерительный шум считаются гауссовыми, то есть:
(0,Rk)
Следовательно, ковариационная матрица может быть непосредственно распространена между шагами измерения с использованием линейного алгебраического уравнения как:
AkPk 'kAkT + Qk
Коррекционные уравнения для обновления измерения:
Pk + 1 | k + 1 = (I − KkHk) Pk + 1 | k
Чтобы вычислить матрицу усиления Калмана (Kk) в каждом обновлении, фильтру необходимо вычислить обратную матрицу:
1HkT + Rk] − 1
Поскольку размерность инвертированной матрицы равна размерности оцененного состояния, этот расчет требует некоторых вычислительных усилий для высокоразмерной системы. Дополнительные сведения см. в разделе Линейные фильтры Калмана.
Альфа-бета-фильтр (trackingABF) - неоптимальный фильтр, применяемый к линейным системам. Фильтр можно рассматривать как упрощенный фильтр Калмана. В фильтре Калмана матрицы усиления и ковариации Калмана вычисляются динамически и обновляются на каждом шаге. Однако в альфа-бета-фильтре эти матрицы постоянны. Эта обработка приносит в жертву оптимальность фильтра Калмана, но повышает эффективность вычислений. По этой причине альфа-бета-фильтр может быть предпочтительным, когда ресурсы вычисления ограничены.
Самый популярный расширенный фильтр Кальмана (trackingEKF) модифицирована из классического фильтра Калмана для адаптации к нелинейным моделям. Он работает путем линеаризации нелинейной системы относительно оценки состояния и игнорирования нелинейных членов второго и более высокого порядка. Его формулировки в основном те же, что и у линейного фильтра Калмана, за исключением того, что матрицы Ak и Hk в фильтре Калмана заменены матрицами якобиана f (xk) и h (xk ):
∂xk'xk'k−1
Если истинная динамика системы оценки близка к линеаризованной динамике, то использование этой линейной аппроксимации не дает существенных ошибок в течение короткого периода времени. По этой причине EKF может производить относительно точные оценки состояния для мягко нелинейной системы оценки с короткими интервалами обновления. Однако, поскольку EKF пренебрегает членами более высокого порядка, он может расходиться для высоконелинейных систем (например, квадроторов), особенно с большими интервалами обновления.
По сравнению с KF, EKF необходимо вывести матрицы якобиана, что требует, чтобы динамика системы была дифференцируемой, и вычислить матрицы якобиана для линеаризации системы, которая требует больше вычислительных активов.
Обратите внимание, что для систем оценки с состоянием, выраженным в сферических координатах, можно использовать trackingMSCEKF.
Незараженный фильтр Кальмана (trackingUKF) использует некачественное преобразование (UT) для приблизительно распространения ковариационного распределения для нелинейной модели. UT-подход производит выборку ковариационного гауссова распределения в текущее время, распространяет точки выборки (называемые сигма-точками) с использованием нелинейной модели и аппроксимирует результирующее ковариационное распределение, предполагаемое гауссовым, оценивая эти распространенные сигма-точки. Фигура иллюстрирует разницу между фактическим распространением, линеаризованным распространением и UT распространением ковариации неопределенности.
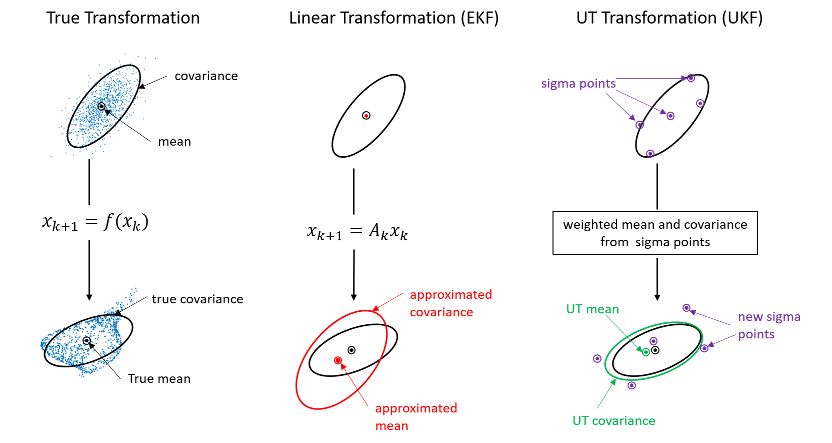
По сравнению с подходом линеаризации, принятым EKF, подход UT приводит к более точному распространению ковариации и приводит к более точной оценке состояния, особенно для высоколинейных систем. UKF не требует деривации и вычисления якобианских матриц. Однако UKF требует распространения 2n + 1 сигма-точек через нелинейную модель, где n - размерность оценочного состояния. Это может быть дорогостоящим в вычислительном отношении для высокоразмерных систем.
Кубатурный фильтр Кальмана (trackingCKF) использует несколько иной подход, чем UKF, для генерации 2n точек выборки, используемых для распространения ковариационного распределения, где n - размерность оцененного состояния. Этот альтернативный набор точек выборки часто приводит к лучшей статистической стабильности и избегает расхождений, которые могут возникнуть в UKF, особенно при работе на платформе с одной точностью. Заметим, что CKF, по существу, эквивалентен UKF, когда параметры UKF установлены в α = 1, β = 0 и ((()) = 0. Посмотрите trackingUKF для определения этих параметров.
Фильтр Гауссова-Суммы (trackingGSF) использует взвешенную сумму множественных гауссовых распределений для аппроксимации распределения оценочного состояния. Оценочное состояние задаётся взвешенной суммой гауссовых состояний:
где N - число гауссовых состояний, сохраняемых в фильтре, а cki - вес соответствующего гауссова состояния, который изменяется в каждом обновлении на основе измерений. Множественные гауссовы состояния следуют той же динамической модели, что и:
1,2,..., N.
Фильтр эффективен при оценке состояний не полностью наблюдаемой системы оценки. Например, фильтр может использовать несколько расширенных фильтров Калмана, параметризованных углом, для оценки состояния системы, когда доступны только измерения диапазона. Пример см. в разделе Отслеживание измерений только по диапазону.
Интерактивный фильтр нескольких моделей (trackingIMM) использует несколько гауссовых фильтров для отслеживания положения цели. В системах с высокой маневренностью динамика системы может переключаться между несколькими моделями (например, постоянная скорость, постоянное ускорение и постоянный поворот). Моделирование движения цели с использованием только одной модели движения затруднено. Система оценки множества моделей может быть описана как:
xki, vki)
где i = 1, 2,..., M и M - общее число динамических моделей. Фильтр IMM разрешает неопределенность движения цели, используя несколько моделей для маневрирующей цели. Фильтр обрабатывает все модели одновременно и представляет общую оценку как взвешенную сумму оценок из этих моделей, где весами являются вероятности каждой модели. Пример см. в разделе Отслеживание маневренных целей.
Фильтр частиц (trackingPF) отличается от семейства фильтров Калмана (например, EKF и UKF), так как не опирается на предположение о распределении Гаусса, которое соответствует параметрическому описанию неопределенностей с использованием среднего и дисперсии. Вместо этого фильтр частиц создает множественные моделирования взвешенных образцов (частиц) работы системы во времени, а затем анализирует эти частицы как прокси для неизвестного истинного распределения. Краткое введение алгоритма фильтра частиц показано на рисунке.
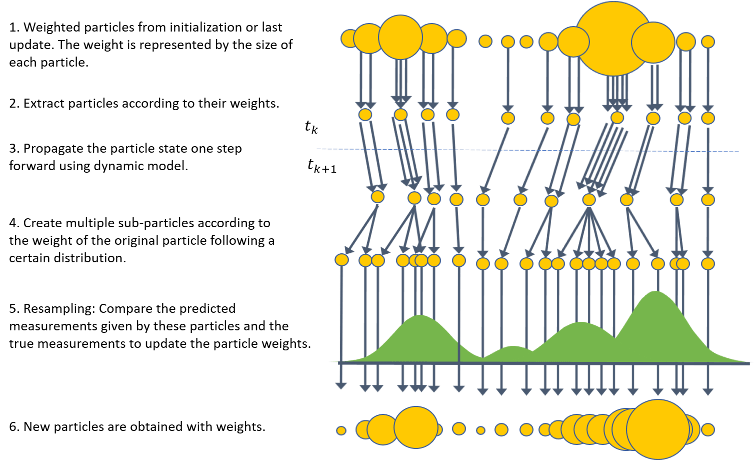
Мотивацией этого подхода является аргумент закона больших чисел - по мере того, как число частиц становится большим, их эмпирическое распределение приближается к истинному распределению. Основное преимущество фильтра частиц перед различными фильтрами Калмана заключается в том, что он может применяться к негауссовым распределениям. Кроме того, фильтр не имеет ограничений на динамику системы и может использоваться с высоконелинейной системой. Другим преимуществом является присущая фильтру способность представлять несколько гипотез о текущем состоянии. Поскольку каждая частица представляет гипотезу о состоянии с определённым связанным правдоподобием, фильтр частиц полезен в случаях, когда существует неоднозначность о состоянии.
Наряду с этими привлекательными свойствами, высокая вычислительная сложность фильтра частиц. Например, UKF требует распространения 13 точек выборки для оценки 3-D положения и скорости объекта. Однако фильтр частиц может потребовать тысячи частиц для получения разумной оценки. Кроме того, количество частиц, необходимое для достижения хорошей оценки, растет очень быстро с измерением состояния и может привести к проблемам лишения частиц в пространствах высоких размеров. Поэтому фильтры частиц в основном применяются к системам с достаточно малым количеством размеров (например, роботы).
В следующей таблице перечислены все фильтры отслеживания, доступные в Sensor Fusion и Tracking Toolbox, и способы их выбора с учетом ограничений нелинейности системы, распределения состояний и сложности вычислений.
| Имя фильтра | Поддержка нелинейных моделей | Гауссовское государство | Вычислительная сложность | Комментарии |
| Альфа-Бета | Низко | Неоптимальный фильтр. | ||
| Кальман | ✓ | Средний низкий | Оптимален для линейных систем. | |
| Расширенный Кальман | ✓ | ✓ | Среда | Использует линеаризованные модели для распространения ковариации неопределенности. |
| Незатронутый Кальман | ✓ | ✓ | Средняя высота | Выполняет выборку ковариации неопределенности для распространения точек выборки. Может стать численно нестабильным в платформе с одинарной точностью. |
| Кубатура Кальман | ✓ | ✓ | Средняя высота | Выполняет выборку ковариации неопределенности для распространения точек выборки. Численно стабильный. |
| Гауссова сумма | ✓ | ✓ (Предполагает взвешенную сумму распределений) | Высоко | Хорошо для частично наблюдаемых случаев (например, отслеживание только под углом). |
| Взаимодействие нескольких моделей (IMM) | ✓ Несколько моделей | ✓ (Предполагает взвешенную сумму распределений) | Высоко | Маневрирование объектами (например, которые ускоряются или поворачиваются) |
| Частица | ✓ | Очень высокий | Выборка распределения неопределенности с использованием взвешенных частиц. |
[1] Ван, Э.А. и Р. Ван Дер Мерве. «Незаметный фильтр Калмана для нелинейной оценки». IEEE 2000 Адаптивные системы для обработки сигналов, связи и симпозиума по управлению. № 00EX373, 2000, стр 153–158.
[2] Фан, Х., Н. Тянь, Я. Ван, М. Чжоу и М. А. Хайле. «Нелинейная байесовская оценка: от фильтрации Калмана до более широкого горизонта». IEEE/CAA Journal of Automatica Sinica. Том 5, номер 2, 2018, стр. 401-417.
[3] Арасаратнам, И. и С. Хайкин. «Кубатурные фильтры Калмана». Транзакции IEEE при автоматическом управлении. Том 54, номер 6, 2009, стр. 1254-1269.
[4] Конатовский, С., П. Каниевский и Я. Матушевский. «Сравнение точности оценки фильтров EKF, UKF и PF». Ежегодник мореплавания. Том 23, номер 1, 2016, стр. 69-87.
[5] Дарко, Дж. «Отслеживание объектов: фильтр частиц с легкостью». https://www.codeproject.com/Articles/865934/Object-Tracking-Particle-Filter-with-Ease.