gamultiobj АлгоритмВ этом разделе описывается алгоритм, gamultiobj используется для создания набора точек на передней панели Парето. gamultiobj использует управляемый, элитарный генетический алгоритм (вариант NSGA-II [3]). Элитарная ГА всегда отдает предпочтение лицам с лучшей фитнес-ценностью (рангом). Контролируемая элитарная ГА также отдает предпочтение лицам, которые могут помочь увеличить разнообразие населения, даже если они имеют более низкую ценность для фитнеса.
Большая часть терминологии для gamultiobj алгоритм аналогичен терминологии генетического алгоритма. Однако существуют некоторые дополнительные термины, описанные в этом разделе. Подробнее о терминологии и алгоритме см. Deb [3].
Доминирование - точка x доминирует над точкой y для векторной целевой функции f, когда:
fi (x) ≤ fi (y) для всех i.
fj (x) < fj (y) для некоторых j.
Термин «доминировать» эквивалентен термину «уступать:» x доминирует над y именно тогда, когда y уступает x.
Недоминированное множество среди множества точек P - это множество точек Q в P, в которых не доминирует ни одна точка в P.
Ранг - для возможных индивидуумов существует итеративное определение ранга индивидуума. В особях 1 ранга не доминируют какие-либо другие особи. В особях 2 ранга доминируют только особи 1 ранга. В общем, чин k особи доминируют только особи в ранге k - 1 или ниже.
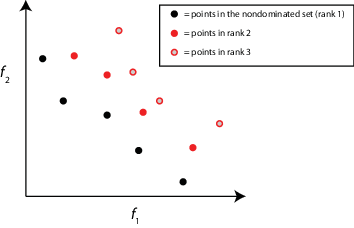
Лица с более низким рангом имеют более высокие шансы на отбор (более низкий ранг лучше).
У всех неосуществимых индивидуумов ранг хуже, чем у любого выполнимого индивидуума. В пределах неосуществимой популяции рангом является порядок по отсортированной мере несходимости плюс высший ранг для возможных членов.
gamultiobj использует ранг для выбора родителей.
Расстояние переполнения - расстояние переполнения является мерой близости человека к ближайшим соседям. gamultiobj алгоритм измеряет расстояние между лицами одного ранга. По умолчанию алгоритм измеряет расстояние в пространстве целевой функции. Однако можно измерить расстояние в пространстве переменных принятия решений (называемом также пространством конструктивных переменных), задав значение DistanceMeasureFcn опция для {@distancecrowding,'genotype'}.
Алгоритм устанавливает расстояние отдельных лиц в крайних положениях на Inf. Для остальных особей алгоритм вычисляет расстояние как сумму по размерностям нормированных абсолютных расстояний между отсортированными соседями индивидуума. Другими словами, для измерения m и отсортированные, масштабированные отдельные i:
distance(i) = sum_m(x(m,i+1) - x(m,i-1)).
Алгоритм сортирует каждое измерение отдельно, поэтому термин «соседи» означает соседей в каждом измерении.
Особи одного ранга с более высокой дистанцией имеют более высокие шансы на отбор (более высокая дистанция лучше).
Можно выбрать другое измерение расстояния переполнения, чем по умолчанию @distancecrowding функция. См. раздел Параметры многообъективности.
Расстояние переполнения является одним из факторов при расчете разброса, который является частью критерия остановки. Дистанция переполнения также используется как тай-брейкер в турнирном отборе, когда два выбранных человека имеют одинаковый ранг.
Спред - спред является мерой движения множества Парето. Чтобы вычислить спред, gamultiobj алгоритм сначала оценивает λ, стандартное отклонение измерения расстояния переполнения точек, которые находятся на фронте Парето с конечным расстоянием. Q - количество этих точек, и d - среднее измерение расстояния между этими точками. Затем алгоритм вычисляет λ, сумму по индексам k целевой функции нормы разности между текущей точкой Парето минимального значения для этого индекса и минимальной точкой для этого индекса в предыдущей итерации. Затем разброс
spread = (λ + λ )/( λ + Qd).
Разброс мал, когда значения предельной целевой функции мало меняются между итерациями (то есть λ мал) и когда точки на фронте Парето разбросаны равномерно (то есть λ мал).
gamultiobj использует спред в состоянии остановки. Итерации останавливаются, когда разброс не сильно меняется, а конечный разброс меньше среднего из последних спредов. См. раздел Условия остановки.
Первый шаг в gamultiobj алгоритм создает начальное заполнение. Алгоритм создает заполнение, или можно дать начальное заполнение или частичное начальное заполнение, используя InitialPopulationMatrix (см. раздел «Параметры заполнения»). Количество лиц в популяции устанавливается как значение PopulationSize вариант. По умолчанию gamultiobj создает совокупность, выполнимую в отношении границ и линейных ограничений, но необязательно выполнимую в отношении нелинейных ограничений. Алгоритм создания по умолчанию: @gacreationuniform при отсутствии зависимостей или только ограничивающих зависимостей, и @gacreationlinearfeasible при наличии линейных или нелинейных ограничений.
gamultiobj оценивает целевую функцию и ограничения для населения и использует эти значения для создания оценок для населения.
Основная итерация gamultiobj алгоритм работает следующим образом.
Выберите родители для следующего поколения с помощью функции выбора для текущей совокупности. Единственная встроенная функция выбора, доступная для gamultiobj является бинарным турниром. Можно также использовать пользовательскую функцию выбора.
Создание потомков из выбранных родителей по мутации и кроссоверу.
Оцените детей, рассчитав их значения целевой функции и выполнимость.
Объедините текущую популяцию и детей в одну матрицу, расширенную популяцию.
Рассчитать ранг и дистанцию скопления для всех лиц в расширенной популяции.
Обрезать расширенное заполнение, чтобы иметь PopulationSize лиц, сохранив соответствующее количество лиц каждого ранга.
Применяются следующие условия остановки. Каждое условие остановки связано с флагом выхода.
| значение exitflag | Условие остановки |
|---|---|
1 | Среднее геометрическое относительного изменения значения разброса по |
0 | Превышено максимальное число поколений |
-1 | Оптимизация завершается функцией вывода или функцией графика |
-2 | Выполнимая точка не найдена |
-5 | Превышен лимит времени |
Для флага выхода 1 среднее геометрическое относительное изменение разброса имеет множитель ½ k для относительного изменения в k-ом предыдущем поколении.
[1] Цензор, Y. «Оптимальность Парето в многообъективных проблемах», Appl. Math. Optimiz., Vol. 4, pp. 41-59, 1977.
[2] Да Кунья, Н. О. и Э. Полак. «Ограниченная минимизация при векторных критериях в конечных пространствах», J. Math. Anal. Appl., Vol. 19, pp. 103-124, 1967.
[3] Деб, Калянмой. «Многообъектная оптимизация с использованием эволюционных алгоритмов», John Wiley & Sons, Ltd, Chichester, England, 2001.
[4] Zadeh, L.A. «Оптимальность и нескалярные критерии производительности», IEEE Trans. Automat. Контр., т. AC-8, с. 1, 1963.