Exponenta Banner
exponenta event banner

Что такое многообъективная оптимизация?

Может потребоваться сформулировать проблемы с несколькими целями, поскольку одна цель с несколькими ограничениями может неадекватно представлять проблему. Если да, то существует вектор целей,

F (x) = [F1 (x), F2 (x),..., Fm (x)],(1)
это нужно каким-то образом обменять. Относительная важность этих целей в целом неизвестна до тех пор, пока не будут определены наилучшие возможности системы и не будут полностью поняты компромиссы между этими целями. По мере увеличения числа целей компромиссы, вероятно, станут сложными и менее легко поддающимися количественной оценке. Дизайнер должен полагаться на свою интуицию и способность выражать предпочтения в течение всего цикла оптимизации. Таким образом, требования к многообъективной стратегии проектирования должны позволять выражать естественную постановку проблемы и быть способными решать проблему и вводить предпочтения в численно прослеживаемую и реалистичную задачу конструирования.

Многообъективная оптимизация связана с минимизацией вектора целей F (x), который может быть объектом ряда ограничений или ограничений:

minx∈ℝnF (x) , субъект toGi (x)  = 0, i = 1,. .., ke;  Gi (x) ≤0, i =  ke + 1,..., k; l≤x≤u.

Заметим, что поскольку F (x) является вектором, если какой-либо из компонентов F (x) конкурирует, уникального решения этой задачи не существует. Вместо этого для характеристики целей следует использовать концепцию неинформативности в Заде [4] (также называемую оптимальностью Парето в Цензоре [1] и Да Кунья и Полаке [2]). Неинферитивным решением является решение, в котором улучшение одной цели требует деградации другой. Чтобы более точно определить это понятие, рассмотрим выполнимую область Λ в пространстве параметров. x - элемент n-мерных вещественных чисел x∈ℝn который удовлетворяет всем ограничениям, то есть

Ω={x∈ℝn},

подлежит

Gi (x) = 0, i = 1,..., ke,  Gi (x) ≤0, i = ke + 1,..., k,l≤x≤u.

Это позволяет определить соответствующую осуществимую область для пространства Λ целевой функции:

Λ={y∈ℝm:y=F (x), x∈Ω}.

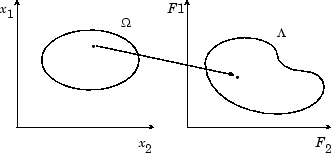
Вектор производительности F (x) отображает пространство параметров в пространство целевой функции, как показано в двух измерениях на рис. 9-1, Отображение из пространства параметров в пространство целевой функции.

Рис. 9-1, Отображение из пространства параметров в пространство целевой функции

Теперь может быть определена точка решения, не связанная с обработкой.

Определение: Точка x*∈Ω является решением, не нарушающим правила, если для некоторой окрестности x * не существует Δx такой, что (x * + Δx) ∈Ω и

Fi (x * + Δx) ≤Fi (x *), i = 1,..., m, и Fj (x  * + Δx) < Fj (x *) по меньшей мере для одного j.

В двумерном представлении на рис. 9-2, Набор решений для неинферьеров, набор решений для неинферьеров лежит на кривой между точками C и D. Точки A и B представляют конкретные точки для неинферьеров.

Рис. 9-2, Набор решений Noninferior

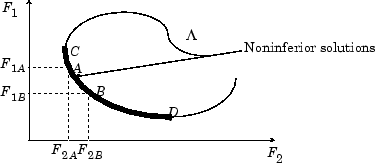
A и B являются явно неубедительными точками решения, поскольку улучшение одной цели, F1, требует ухудшения другой цели, F2, то есть F1B  < F1A, F2B  > F2A.

Поскольку любая точка в Ом, которая является нижней точкой, представляет собой точку, в которой может быть достигнуто улучшение во всех задачах, ясно, что такая точка не имеет значения. Таким образом, многообъективная оптимизация связана с генерированием и выбором точек решения, отличных от других.

Noninferior решения также называются Pareto optima. Общей целью многообъективной оптимизации является построение оптимизации Парето.

Связанные темы

Документация по инструментам глобальной оптимизации

Поддержка