ga Оптимизацияga может решить проблемы, если некоторые переменные являются целочисленными. Дать IntCon, вектор из x компонентов, которые являются целыми числами:
[x,fval,exitflag] = ga(fitnessfcn,nvars,A,b,[],[],...
lb,ub,nonlcon,IntCon,options)IntCon - вектор положительных целых чисел, содержащий компоненты x, которые являются целочисленными. Например, если требуется ограничить x(2) и x(10) быть целыми числами, установить IntCon кому [2,10].
surrogateopt решатель также принимает целочисленные ограничения.
Примечание
Существуют ограничения на типы проблем, которые ga может решаться целочисленными переменными. В частности, ga не допускает никаких ограничений равенства при наличии целочисленных переменных. Дополнительные сведения см. в разделе Характеристики целочисленного решателя ga.
Совет
ga решает целочисленные задачи лучше всего, если для каждого компонента x предусмотрены нижние и верхние границы.
В этом примере показано, как найти минимальное ограничение функции Растригина, так что первый компонент x является целым числом. Компоненты x также ограничены находиться в области ) ≤-4π.
Настройка границ для проблемы
lb = [5*pi,-20*pi]; ub = [20*pi,-4*pi];
Задайте функцию графика, чтобы можно было просматривать ход выполнения ga
opts = optimoptions('ga','PlotFcn',@gaplotbestf);
Вызовите решатель ga, где x (1) имеет целочисленные значения
rng(1,'twister') % for reproducibility IntCon = 1; [x,fval,exitflag] = ga(@rastriginsfcn,2,[],[],[],[],... lb,ub,[],IntCon,opts)

Optimization terminated: average change in the penalty fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
x = 1×2
16.0000 -12.9325
fval = 424.1355
exitflag = 1
ga быстро сходится к решению.
Существуют некоторые ограничения на типы проблем, которые ga можно решить, если включить целочисленные ограничения:
Нет ограничений линейного равенства. Вы должны иметь Aeq = [] и beq = []. Возможные варианты обхода см. в разделе Отсутствие ограничений равенства.
Нет нелинейных ограничений равенства. Любая нелинейная функция ограничения должна быть возвращена [] для ограничения нелинейного равенства. Возможные варианты обхода см. в разделе Пример: Целочисленное программирование с ограничением нелинейного равенства.
Только doubleVector тип популяции.
Нет пользовательской функции создания (CreationFcn опция), функция кроссовера (CrossoverFcn вариант), мутационная функция (MutationFcn вариант) или начальные баллы (InitialScoreMatrix опция). Если вы поставляете что-либо из этого, ga переопределяет их параметры.
ga использует только двоичную функцию выбора турнира (SelectionFcn ) и переопределяет любую другую настройку.
Гибридная функция отсутствует. ga переопределяет любую настройку HybridFcn вариант.
ga игнорирует ParetoFraction, DistanceMeasureFcn, InitialPenalty, и PenaltyFactor варианты.
Перечисленные ограничения являются в основном естественными, а не произвольными. Например:
Гибридные функции, поддерживающие целочисленные ограничения, отсутствуют. Так ga не использует гибридные функции при наличии целочисленных ограничений.
Чтобы получить целочисленные переменные, ga использует специальные функции создания, кроссовера и мутации.
В одной проблеме нельзя использовать ограничения равенства и целочисленные ограничения. Можно попытаться обойти это ограничение, включив два ограничения неравенства для каждого линейного ограничения равенства. Например, чтобы попытаться включить ограничение
3x1 – 2x2 = 5,
создать два ограничения неравенства:
3x1 – 2x2 ≤ 5
3x1 – 2x2 ≥ 5.
Чтобы записать эти ограничения в форму A x ≤ b, умножить второе неравенство на -1:
– 3x1 + 2x2 ≤ –5.
Можно попытаться включить ограничение равенства, используя A = [3,-2;-3,2] и b = [5;-5].
Помните, что эта процедура может завершиться ошибкой; ga имеет трудности с одновременными целочисленными ограничениями и ограничениями равенства.
Пример: Целочисленное программирование с нелинейным ограничением равенства. В этом примере предпринимается попытка найти минимум функции Ackley (входящей в состав программного обеспечения) в пяти измерениях со следующими ограничениями:
x(1), x(3), и x(5) являются целыми числами.
norm(x) = 4.
Функцию Акли трудно минимизировать. Добавление целочисленных ограничений и ограничений равенства увеличивает сложность.
Чтобы включить ограничение нелинейного равенства, задайте небольшой допуск tol что позволяет норму x находиться в пределах tol из 4. Без допуска ограничение нелинейного равенства никогда не выполняется, и решатель не осознает, когда у него есть выполнимое решение.
Записать выражение norm(x) = 4 как два неравенства «меньше нуля»:
norm(x) - 4 ≤ 0
-(norm(x) - 4) ≤ 0.
Допускайте малую терпимость к неравенствам:
norm(x) - 4 - tol ≤ 0
-(norm(x) - 4) - tol ≤ 0.
Запишите функцию ограничения нелинейного неравенства, которая реализует эти неравенства:
function [c, ceq] = eqCon(x)
ceq = [];
rad = 4;
tol = 1e-3;
confcnval = norm(x) - rad;
c = [confcnval - tol;-confcnval - tol];Задать параметры:
MaxStallGenerations = 50 - Разрешить решателю пробовать некоторое время.
FunctionTolerance = 1e-10 - Укажите более строгий критерий остановки, чем обычно.
MaxGenerations = 300 - Разрешить больше поколений, чем по умолчанию.
PlotFcn = @gaplotbestfun - Наблюдать за оптимизацией.
opts = optimoptions('ga','MaxStallGenerations',50,'FunctionTolerance',1e-10,... 'MaxGenerations',300,'PlotFcn',@gaplotbestfun);
Установите нижние и верхние границы, чтобы помочь решателю:
nVar = 5; lb = -5*ones(1,nVar); ub = 5*ones(1,nVar);
Решите проблему:
rng(0,'twister') % for reproducibility [x,fval,exitflag] = ga(@ackleyfcn,nVar,[],[],[],[], ... lb,ub,@eqCon,[1 3 5],opts);
Optimization terminated: average change in the penalty fitness value less than options.FunctionTolerance and constraint violation is less than options.ConstraintTolerance.
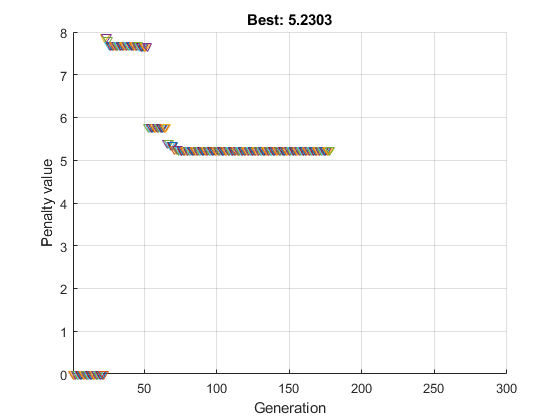
Осмотрите решение:
x,fval,exitflag,norm(x)
x =
0 -1.7367 -3.0000 -0.0000 -2.0000
fval =
5.2303
exitflag =
1
ans =
4.0020Странное x компоненты являются целыми числами, как указано. Норма x является 4, в пределах заданного относительного допуска 1e-3.
Несмотря на положительный флаг выхода, решение не является глобальным оптимумом. Запустите проблему еще раз и изучите решение:
opts = optimoptions('ga',opts,'Display','off'); [x2,fval2,exitflag2] = ga(@ackleyfcn,nVar,[],[],[],[], ... lb,ub,@eqCon,[1 3 5],opts);
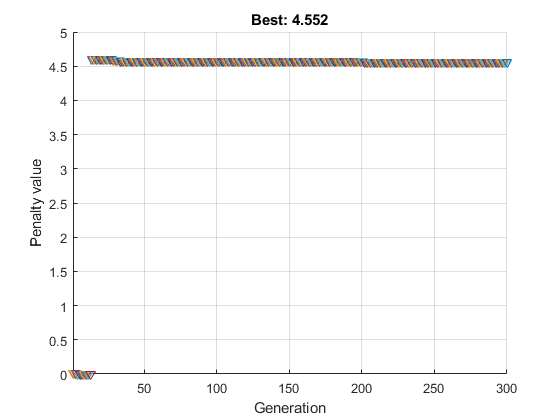
Осмотрите второе решение:
x2,fval2,exitflag2,norm(x2)
x2 =
-2.0000 2.8930 0 -1.9095 0
fval2 =
4.5520
exitflag2 =
0
ans =
4.0020Второй прогон дает лучшее решение (более низкое значение фитнес-функции). Опять же, нечетное x компоненты являются целыми числами и нормой x2 является 4, в пределах заданного относительного допуска 1e-3.
Помните, что эта процедура может завершиться ошибкой; ga имеет трудности с одновременными целочисленными ограничениями и ограничениями равенства.
gaИспользовать ga наиболее эффективно для целочисленных проблем, следуйте этим рекомендациям.
Соедините каждый компонент как можно плотнее. Эта практика дает ga наименьшее пространство поиска, включение ga для наиболее эффективного поиска.
Если привязать компонент невозможно, укажите соответствующий начальный диапазон. По умолчанию ga создает начальное заполнение с диапазоном [-1e4,1e4] для каждого компонента. Меньший или больший начальный диапазон может дать лучшие результаты, если значение по умолчанию неуместно. Для изменения начального диапазона используйте InitialPopulationRange вариант.
При наличии более 10 переменных задайте размер заполнения, превышающий размер по умолчанию, с помощью PopulationSize вариант. Значение по умолчанию - 200 для шести или более переменных. Для большой численности населения:
ga может занять много времени, чтобы сойтись. При достижении максимального количества поколений (флаг выхода 0), увеличьте значение MaxGenerations вариант.
Уменьшите скорость мутации. Для этого увеличьте значение CrossoverFraction от его значения по умолчанию 0.8 кому 0.9 или выше.
Увеличение значения EliteCount от его значения по умолчанию 0.05*PopulationSize кому 0.1*PopulationSize или выше.
Дополнительные сведения о параметрах см. в разделе ga
options входной аргумент.
ga АлгоритмЦелочисленное программирование с помощью ga включает несколько модификаций базового алгоритма (см. Как работает генетический алгоритм). Для целочисленного программирования:
Специальные функции создания, кроссовера и мутации заставляют переменные быть целыми числами. Подробнее см. Deep et al. [2].
Генетический алгоритм пытается минимизировать функцию штрафа, а не функцию пригодности. Функция штрафа включает термин несходимости. Эта функция штрафа сочетается с бинарным турнирным отбором для выбора индивидуумов для последующих поколений. Значение штрафной функции члена совокупности:
Если элемент осуществим, функция штрафа является функцией пригодности.
Если член является неосуществимым, функция штрафа является функцией максимальной пригодности среди возможных членов популяции плюс сумма нарушений ограничения (неосуществимой) точки.
Для получения подробной информации о функции штрафа см. Deb [1].
ga не применяет линейные ограничения при наличии целочисленных ограничений. Вместо этого ga включает нарушения линейных ограничений в функцию штрафа.
[1] Деб, Калянмой. Эффективный метод обработки ограничений для генетических алгоритмов. Компьютерные методы в прикладной механике и технике, 186 (2-4), стр. 311-338, 2000 .
[2] Дип, Кусум, Кришна Пратап Сингх, М. Л. Кансал и К. Мохан. Настоящий кодированный генетический алгоритм для решения задач целочисленной и смешанной целочисленной оптимизации. Прикладная математика и вычисления, 212 (2), стр. 505-518, 2009.