Векторизация функций цели и ограничения

Векторизация для скорости

Прямой поиск часто выполняется быстрее, если векторизировать целевые и нелинейные функции ограничения. Это означает, что ваши функции вычисляют все точки в шаблоне опроса или поиска одновременно, с помощью одного вызова функции, без необходимости закольцовывать точки по одному. Поэтому вариант UseVectorized = true работает только тогда, когда UseCompletePoll или UseCompleteSearch также имеет значение true. Однако при установке UseVectorized = true, patternsearch проверяет, чтобы целевая и любая нелинейная функции ограничения давали выходы правильной формы для векторизированных вычислений, независимо от установки UseCompletePoll или UseCompleteSearch варианты.

Если существуют нелинейные ограничения, целевая функция и нелинейные ограничения должны быть векторизированы, чтобы алгоритм мог вычисляться векторизированным образом.

Примечание

Запишите векторизированную целевую функцию или нелинейную функцию ограничения, чтобы принять матрицу с произвольным числом точек. patternsearch иногда вычисляет одну точку даже во время векторизованного вычисления.

Векторизованная целевая функция

Векторизированная целевая функция принимает матрицу в качестве входных данных и генерирует вектор значений функций, где каждое значение функции соответствует одной строке или столбцу входной матрицы. patternsearch разрешает неоднозначность в том, представляют ли строки или столбцы матрицы точки шаблона следующим образом. Предположим, что входная матрица имеет m строки и n столбцы:

Если начальная точка x0 - вектор столбца размера m, целевая функция принимает каждый столбец матрицы в качестве точки в шаблоне и возвращает вектор строки размера n.
Если начальная точка x0 - вектор строки размера n, целевая функция принимает каждую строку матрицы в качестве точки в шаблоне и возвращает вектор столбца размера m.
Если начальная точка x0 является скаляром, patternsearch предполагает, что x0 - вектор строки. Поэтому входная матрица имеет один столбец (n = 1, входная матрица является вектором), и каждая запись матрицы представляет одну строку для целевой функции для вычисления. Выводом целевой функции в этом случае является вектор столбца размера m.

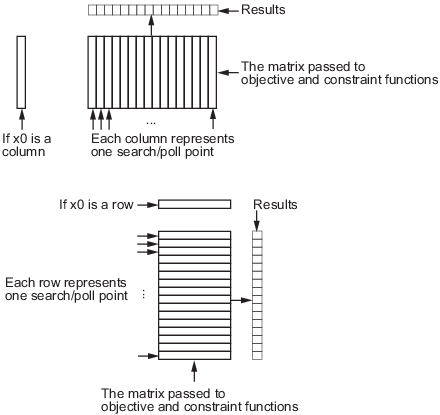
Графически матрица и расчет представлены на следующем рисунке.

Структура векторизированных функций

Например, предположим, что целевая функция

$f (x)_{=}^{}_{x14}^{} +_{}^{x24} −_{}^{} 4x12_{−}_{} 2x22$ + 3x1 − x2/2.

Если начальный вектор x0 является вектором-столбцом, таким как [0;0], функция векторизированной оценки

function f = vectorizedc(x)

f = x(1,:).^4+x(2,:).^4-4*x(1,:).^2-2*x(2,:).^2 ...
    +3*x(1,:)-.5*x(2,:);

Если начальный вектор x0 - вектор строки, например, [0,0], функция векторизированной оценки

function f = vectorizedr(x)

f = x(:,1).^4+x(:,2).^4-4*x(:,1).^2-2*x(:,2).^2 ...
    +3*x(:,1)-.5*x(:,2);

Совет

Если вы хотите использовать одну и ту же целевую (фитнес) функцию как для поиска шаблона, так и для генетического алгоритма, запишите свою функцию, чтобы точки были представлены векторами строк, и запишите x0 как вектор строки. Генетический алгоритм всегда принимает индивидуумов в качестве строк матрицы. Это было дизайнерское решение - генетический алгоритм не требует поставляемой пользователем популяции, поэтому необходимо иметь формат по умолчанию.

Минимизировать vectorizedcвведите следующие команды:

options=optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
x0=[0;0];
[x,fval]=patternsearch(@vectorizedc,x0,...
         [],[],[],[],[],[],[],options)

MATLAB ® возвращает следующие выходные данные:

Optimization terminated: mesh size less than options.MeshTolerance.

x =
   -1.5737
    1.0575

fval =
  -10.0088

Векторизованные функции ограничения

Векторизируются только нелинейные ограничения; границы и линейные ограничения обрабатываются автоматически. Если существуют нелинейные ограничения, целевая функция и нелинейные ограничения должны быть векторизированы, чтобы алгоритм мог вычисляться векторизированным образом.

Для функций ограничения используются те же соображения, что и для целевых функций: начальная точка x0 определяет тип точек (векторы строк или столбцов) в опросе или поиске. Если начальная точка является вектором строки размера k, матрица x, переданная функции ограничения, имеет k столбцов. Аналогично, если начальная точка является вектором столбца размера k, матрица точек опроса или поиска имеет k строк. Это может быть ясно показано на рисунке Структура векторизированных функций. Если начальная точка является скаляром, patternsearch предполагает, что это вектор строки.

Нелинейная функция ограничения возвращает две матрицы, одну для ограничений неравенства и одну для ограничений равенства. Предположим, что существуют ограничения нелинейного неравенства nc и ограничения нелинейного равенства _nceq. Для вектора строки x0, матрицы ограничений имеют столбцы _nc и _nceq соответственно, и число строк такое же, как во входной матрице. Аналогично, для вектора столбца x0, матрицы ограничений имеют _{строки nc} и _nceq соответственно, и количество столбцов такое же, как во входной матрице. На рисунке Структура векторизированных функций «Результаты» включают nc и _nceq.

Пример векторизованной цели и ограничений

Предположим, что нелинейные ограничения

$\begin{matrix} \frac{_{}^{}}{} \frac{_{}^{}}{} x129+x224≤1 (внутренняя часть эллипса), \\ _{} x2\geqcosh_{(} x1) \end{matrix}$ − 1.

Запись функции для этих ограничений для строковой формы x0 следующим образом:

function [c ceq] = ellipsecosh(x)

c(:,1)=x(:,1).^2/9+x(:,2).^2/4-1;
c(:,2)=cosh(x(:,1))-x(:,2)-1;
ceq=[];

Минимизировать vectorizedr (определяется в векторизованной целевой функции) с учетом ограничений ellipsecosh:

x0=[0,0];
options = optimoptions('patternsearch','UseVectorized',true,'UseCompletePoll',true);
[x,fval] = patternsearch(@vectorizedr,x0,...
         [],[],[],[],[],[],@ellipsecosh,options)

MATLAB возвращает следующие выходные данные:

Optimization terminated: mesh size less than options.MeshTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =
   -1.3516    1.0612

fval =
   -9.5394

Документация