Преобразование многоугольника области интереса (ROI) в маску области
BW = poly2mask(xi,yi,m,n)BW, размера mоколо-n, из многоугольника окупаемости инвестиций с вершинами в координатах xi и yi. Если полигон еще не замкнут, то poly2mask автоматически закрывает полигон.
poly2mask устанавливает пикселы, находящиеся внутри полигона, в 1 и устанавливает пикселы вне полигона в 0. Дополнительные сведения о классификации пикселей, которые частично заключены в ROI, см. в разделе Алгоритм.
Укажите координаты X и Y многоугольника.
x = [63 186 54 190 63]; y = [60 60 209 204 60];
Создайте маску, задающую размер изображения.
bw = poly2mask(x,y,256,256);
Отображение маски, рисование линии вокруг многоугольника.
imshow(bw) hold on plot(x,y,'b','LineWidth',2) hold off
Определите два набора случайных точек для координат x и y.
x = 256*rand(1,4); y = 256*rand(1,4); x(end+1) = x(1); y(end+1) = y(1);
Создайте маску.
bw = poly2mask(x,y,256,256);
Отобразить маску и нарисовать линию вокруг многоугольника.
imshow(bw) hold on plot(x,y,'b','LineWidth',2) hold off
Чтобы задать многоугольник, включающий данный прямоугольный набор пикселов, вместо центра пикселов сделайте края многоугольника лежащими вдоль внешних краев ограничивающих пикселов.
Например, чтобы включить пикселы в столбцы 4-10 и строки 4-10, можно задать вершины многоугольника следующим образом:
x = [4 10 10 4 4]; y = [4 4 10 10 4]; mask = poly2mask(x,y,12,12)
mask =
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0В этом примере многоугольник проходит через центр ограничивающих пикселей, в результате чего только некоторые из требуемых ограничивающих пикселей определяются как находящиеся внутри многоугольника (пиксели в строке 4 и столбце 4, а не в многоугольнике). Чтобы включить эти элементы в многоугольник, используйте дробные значения, чтобы указать внешнюю кромку 4-й строки (3.5) и 10-й строки (10.5), а также внешнюю кромку 4-го столбца (3.5) и внешнюю кромку 10-го столбца (10.5) в качестве вершин, как в следующем примере:
x = [3.5 10.5 10.5 3.5 3.5]; y = [3.5 3.5 10.5 10.5 3.5]; mask = poly2mask(x,y,12,12)
mask =
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0
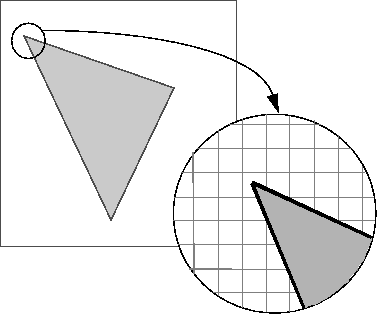
0 0 0 0 0 0 0 0 0 0 0 0При создании маски области интересов (ROI) poly2mask должен определить, какие пикселы включены в область. Это определение может быть затруднено, когда пикселы на краю области лишь частично покрыты линией границы. Следующий рисунок иллюстрирует интересующую треугольную область, рассматривая крупным планом одну из вершин ROI. На рисунке показано, как пиксели могут быть частично покрыты границей интересующей области.
Пикселы на краю ROI покрыты границей только частично
Чтобы определить, какие пикселы находятся в области, poly2mask использует следующий алгоритм:
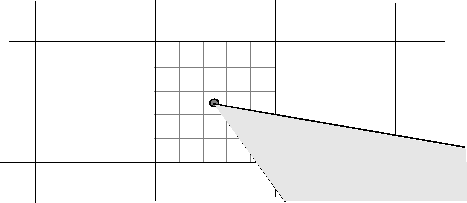
Разделите каждый пиксель на субпиксельную сетку 5 на 5.
На рисунке показан пиксель, который содержит вершину ROI, показанной ранее с этой субпиксельной сеткой 5 на 5.
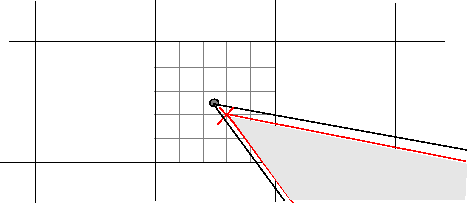
Отрегулируйте положение вершин.
poly2mask перемещает каждую вершину многоугольника к ближайшему пересечению субпиксельной сетки. Обратите внимание, как poly2mask округляет координаты x и y до ближайшего субпиксельного угла сетки. При этом создается второй модифицированный многоугольник. На рисунке показана модифицированная вершина с красным «X».
Нарисуйте траекторию между скорректированными вершинами.
poly2mask формирует путь от каждой скорректированной вершины к следующей, следуя за кромками субпиксельной сетки. На рисунке показана часть этого модифицированного многоугольника толстыми темными линиями.
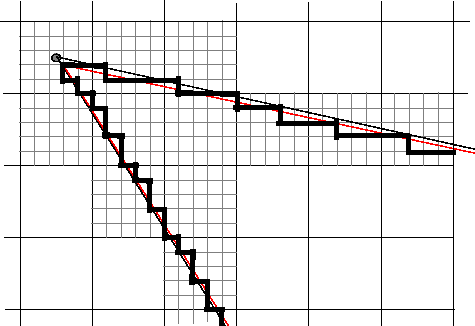
Определите, какие пикселы границы находятся внутри многоугольника.
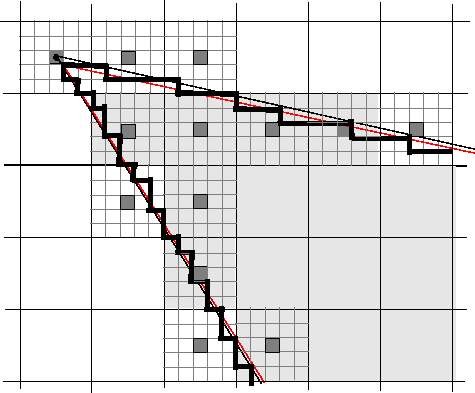
poly2mask использует следующее правило, чтобы определить, какие пикселы границы находятся внутри многоугольника: если центральный субпиксель пикселя находится внутри границ, определяемых путем между скорректированными вершинами, то пиксель находится внутри области.
На следующем рисунке центральные субпиксели пикселей на границе ROI затенены темно-серым цветом. Пикселы внутри многоугольника затенены более светлым серым цветом. Обратите внимание, что пиксель, содержащий вершину, не является частью ROI, поскольку его центральный пиксель не находится внутри модифицированного многоугольника.
