Основная цель навигации состоит в том, чтобы определить в данный момент, как добраться до пункта назначения, избегая опасностей на пути. Первым шагом в достижении этого является установление вашего текущего положения. Ранние моряки держались в пределах видимости земли, чтобы облегчить это. Сегодня навигация в пределах видимости (или радиолокационной дальности) суши называется пилотированием. Положения фиксируются путем корреляции подшипников и/или диапазонов ориентиров. В реальном пилотировании все прицельные подшипники рассматриваются как румбовые линии, в то время как на самом деле они представляют собой большие круги.
На расстояниях, связанных с визуальными наблюдениями (до 20 или 30 морских миль), это предположение не вызывает измеримой ошибки и обеспечивает значительное преимущество, позволяя навигатору строить графики всех подшипников в виде прямых линий на проекции Меркатора.
«Меркатор» был разработан именно для этой цели. Предполагается, что дальномерные круги, которые могут быть определены с помощью радара, отображаются на диаграмме Меркатора как истинные круги. Это позволяет навигатору вручную нарисовать дугу диапазона с помощью компаса.
Эти допущения также приводят к вычислительно эффективным методам фиксации позиций с помощью компьютера. Панель инструментов включает navfix функция, имитирующая процесс ручной печати и фиксации с использованием этих допущений.
Чтобы получить хорошее навигационное исправление, ваше отношение как минимум к трем известным точкам считается необходимым. Сомнительное или плохое исправление может быть получено с двумя известными точками.
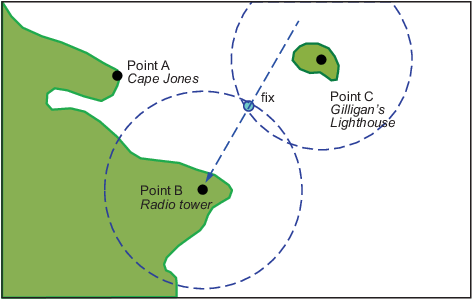
В этой воображаемой прибрежной области вы принимаете визуальный пеленг на радиобашне 270 °. При этом «Маяк Гиллигана» носит 0 °. Если линия 90 ° -270 ° проходит через радиобашню, а линия 0 ° -180 ° - через маяк на диаграмме Меркатора, точка пересечения линий является точкой фиксации. Однако, поскольку вы использовали только две строки, его качество сомнительно.
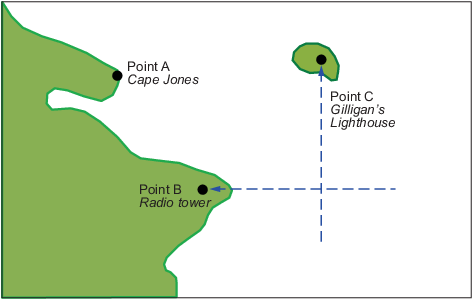
Но подождите; Ваше наблюдение за портом говорит, что он взял на мыс Джонс 300 °. Если эта линия в точности пересекает точку пересечения первых двух линий, у вас будет идеальное исправление.
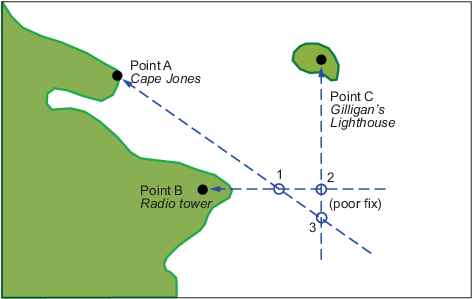
Ой. Что случилось? Ваш поиск ошибочен? Возможно, но, возможно, один или оба ваших подшипника немного ошиблись. Это происходит постоянно. Какой момент, 1, 2 или 3, верен? Насколько вы знаете, все они одинаково действительны.
На практике строится маленький треугольник, и положение фиксации принимается либо центром треугольника, либо вершиной, наиболее близкой к опасности (наподобие мелкой воды). Если треугольник большой, качество сообщается как плохое или даже как отсутствие исправления. Если доступна четвертая линия подшипника, ее можно построить, чтобы попытаться разрешить неоднозначность. Когда все три линии кажутся пересекающимися в одной и той же точке, качество сообщается как отличное или идеальное.
Обратите внимание, что в результате трех линий образовалось три точки пересечения. Четыре линии возвращают шесть точек пересечения. Это случай комбинаторного подсчета. Каждое пересечение соответствует выбору двух линий для пересечения из числа n линий.
В следующий раз, когда вы пересекаете эти проливы, это очень туманное утро. Вы не видите ориентиров, но, к счастью, ваш навигационный радар работает. Каждый из этих ориентиров имеет хорошую радиолокационную подпись, так что ты не волнуешься. Вы получаете дальность от радиобашни 14 морских миль и дальность от маяка 15 морских миль.
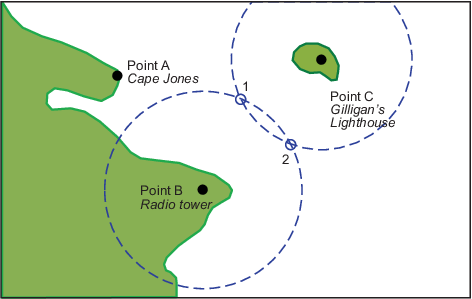
Теперь что? Вы взяли диапазоны только от двух объектов, но у вас есть две возможные позиции. Эта неоднозначность возникает из-за того, что окружности могут пересекаться дважды.
К счастью, ваши радиолокационные часы сообщают, что у него мыс Джонс в 18 морских милях. Это должно решить все.
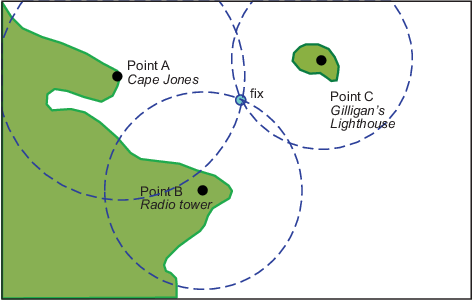
На этот раз тебе повезло. Третий диапазон разрешил неоднозначность и дал вам отличное исправление. Три пересечения практически совпадают. Иногда неоднозначность разрешается, но фиксация все еще бедна, потому что три ближайших пересечения образуют своего рода круговой треугольник.
Иногда третий диапазон только добавляет путаницу, либо деля исходные два варианта пополам, либо вообще не пересекая одну или обе другие дуги. В общем случае, когда используются n дуг, 2x(n-choose-2) результат возможных пересечений. В этом примере легко сказать, какие из них правы.
Опорные линии и дуги могут быть объединены. Если бы вместо сообщения о третьем диапазоне, ваши радиолокационные часы сообщили о пеленге от радарной башни 20 °, неоднозначность также могла бы быть разрешена. Однако следует отметить, что на практике линии пеленга для навигационной фиксации должны приниматься только визуально, за исключением отчаяния. Ширина луча радара может быть не меньше, что приводит к неопределенности.
Когда вы начинаете задумываться, можно ли автоматизировать этот процесс построения графиков вручную, ваш первый сотрудник появляется на мосту с ноутбуком и программным обеспечением Mapping Toolbox™.
navfix navfix может использоваться для определения точек пересечения между любым количеством линий и дуг. Следует, однако, предупредить, что из-за комбинаторного характера этого процесса время вычислений быстро растет с числом объектов. Для иллюстрации этой функции назначьте позиции ориентирам. Точка А, Кейп Джонс, находится в (latA,lonA). Точка B, радиобашня, находится в (latB,lonB). Точка C, маяк Гиллигана, находится в (latC,lonC).
Для примера только для румбов синтаксис:
[latfix,lonfix] = navfix([latA latB latC],[lonA lonB lonC],...
[300 270 0])Это определяет три точки и их подшипники, взятые с корабля. Выходные данные будут выглядеть примерно так, с фактическими числами, конечно:
latfix = latfix1 NaN % A intersecting B latfix2 NaN % A intersecting C latfix3 NaN % B intersecting C lonfix = lonfix1 NaN % A intersecting B lonfix2 NaN % A intersecting C lonfix3 NaN % B intersecting C
Обратите внимание, что это матрицы из двух столбцов. Вторая колонка состоит из NaNs, поскольку он используется только для неоднозначности двух пересечений, связанной с дугами.
Для примера «Только дуги диапазона» синтаксис:
[latfix,lonfix] = navfix([latA latB latC],[lonA lonB lonC],...
[16 14 15],[0 0 0])Это определяет три точки и их диапазоны, взятые из корабля. Последний аргумент указывает, что все три случая являются диапазонами.
Выходные данные имеют следующий вид:
latfix = latfix11 latfix12 % A intersecting B latfix21 latfix22 % A intersecting C latfix31 latfix32 % B intersecting C lonfix = lonfix11 lonfix12 % A intersecting B lonfix21 lonfix22 % A intersecting C lonfix31 lonfix32 % B intersecting C
Здесь используется второй столбец, потому что каждая пара дуг имеет два потенциальных пересечения.
Для примера подшипников и диапазонов синтаксис требует окончательного ввода, чтобы указать, какие объекты являются линиями подшипника (обозначены 1), а какие - дугами диапазона (обозначены 0):
[latfix,lonfix] = navfix([latB latB latC],[lonB lonB lonC],...
[20 14 15],[1 0 0])Полученный результат смешивают:
latfix = latfix11 NaN % Line B intersecting Arc B latfix21 latfix22 % Line B intersecting Arc C latfix31 latfix32 % Arc B intersecting Arc C lonfix = lonfix11 NaN % Line B intersecting Arc B lonfix21 lonfix22 % Line B intersecting Arc C lonfix31 lonfix32 % Arc B intersecting Arc C
Только одно пересечение возвращается для линии от B с дугой около B, так как линия начинается внутри окружности и пересекает её один раз. Одна и та же прямая пересекает другую окружность дважды, и, следовательно, возвращает две точки. Две окружности, взятые вместе, также возвращают две точки.
Как правило, у вас есть представление о том, где вы находитесь, прежде чем принять решение. Например, на момент исправления у вас может быть мертвая позиция расплаты (см. ниже). Если вы предоставите navfix при этом оцененном положении он выбирает из каждой пары неоднозначных пересечений точку, ближайшую к оценке. Вот как это может выглядеть:
[latfix,lonfix] = navfix([latB latB latC],[lonB lonB lonC],...
[20 14 15],[1 0 0],drlat,drlon)latfix = latfix11 % the only point latfix21 % the closer point latfix31 % the closer point lonfix = lonfix11 % the only point lonfix21 % the closer point lonfix31 % the closer point
navfixОпределите некоторые конкретные точки в центре Атлантического океана. Они носят сугубо произвольный характер; возможно, они соответствуют пунктам в Атлантиде:
lata = 3.1; lona = -56.2; latb = 2.95; lonb = -55.9; latc = 3.15; lonc = -55.95;
Постройте их на проекции Меркатора:
axesm('MapProjection','mercator','Frame','on',... 'MapLatLimit',[2.8 3.3],'MapLonLimit',[-56.3 -55.8]) plotm([lata latb latc],[lona lonb lonc],... 'LineStyle','none','Marker','pentagram',... 'MarkerEdgeColor','b','MarkerFaceColor','b',... 'MarkerSize',12)
Вот как это выглядит (с маркировкой и воображаемыми береговыми линиями, добавленными постфактум для иллюстрации):
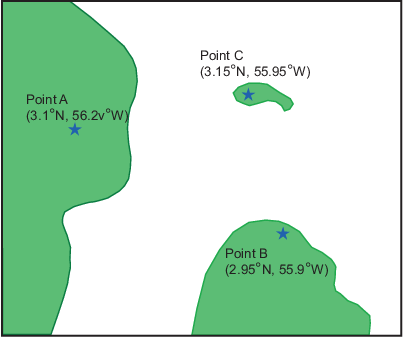
Возьмите три визуальных подшипника: точка A несет 289 °, точка B - 135 °, а точка C - 026,5 °. Вычислите пересечения:
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[289 135 26.5],[1 1 1])newlat = 3.0214 NaN 3.0340 NaN 3.0499 NaN newlong = -55.9715 NaN -56.0079 NaN -56.0000 NaN
Добавьте точки пересечения на карту:
plotm(newlat,newlong,'LineStyle','none',... 'Marker','diamond','MarkerEdgeColor','r',... 'MarkerFaceColor','r','MarkerSize',9)
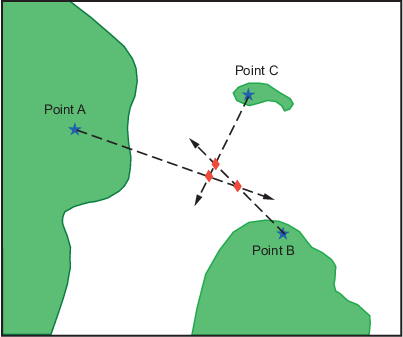
В целях иллюстрации к карте добавлены опорные линии. Обратите внимание, что каждая пара объектов имеет только одно пересечение, поскольку все они являются линиями подшипника.
Что если вместо этого у вас были диапазоны от трех точек, A, B и C, 13 нми, 9 нми и 7,5 нми, соответственно?
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[13 9 7.5],[0 0 0])newlat = 3.0739 2.9434 3.2413 3.0329 3.0443 3.0880 newlong = -55.9846 -56.0501 -56.0355 -55.9937 -56.0168 -55.8413
Вот как выглядят эти моменты:
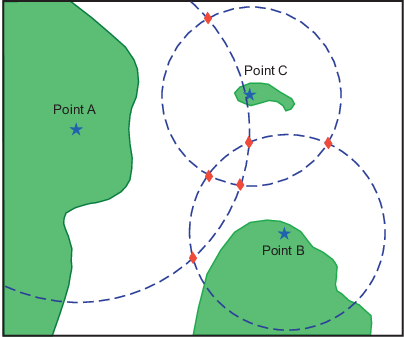
Три из этих пунктов выглядят разумно, три - нет.
Что, если вместо диапазона от точки А у вас был подшипник 284 °?
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[284 9 7.5],[1 0 0])newlat = 3.0526 2.9892 3.0592 3.0295 3.0443 3.0880 newlong = -56.0096 -55.7550 -56.0360 -55.9168 -56.0168 -55.8413
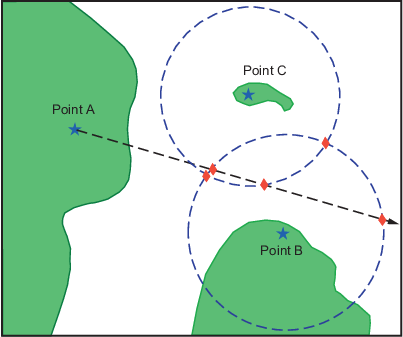
Опять же, визуальный осмотр результатов показывает, какие три из шести возможных пунктов кажутся разумными позициями.
При использовании положения мёртвой расплаты (3,05 ° N, 56,0 ° W) выбирается более близкий, более разумный кандидат от каждой пары пересекающихся объектов:
drlat = 3.05; drlon = -56;
[newlat,newlong] = navfix([lata latb latc],[lona lonb lonc],...
[284 9 7.5],[1 0 0],drlat,drlon)newlat = 3.0526 3.0592 3.0443 newlong = -56.0096 -56.0360 -56.0168