Учитывая математическую функцию одной переменной, можно использовать fminbnd для поиска локального минимизатора функции в заданном интервале. Например, рассмотрим humps.m , которая поставляется с MATLAB ®. На следующем рисунке показан график humps.
x = -1:.01:2; y = humps(x); plot(x,y) xlabel('x') ylabel('humps(x)') grid on

Чтобы найти минимум humps функция в диапазоне (0.3,1), использовать
x = fminbnd(@humps,0.3,1)
x = 0.6370
Подробные сведения о процессе решения можно просмотреть с помощью optimset для создания опций с помощью Display параметр имеет значение 'iter'. Передача результирующих опций в fminbnd.
options = optimset('Display','iter'); x = fminbnd(@humps,0.3,1,options)
Func-count x f(x) Procedure
1 0.567376 12.9098 initial
2 0.732624 13.7746 golden
3 0.465248 25.1714 golden
4 0.644416 11.2693 parabolic
5 0.6413 11.2583 parabolic
6 0.637618 11.2529 parabolic
7 0.636985 11.2528 parabolic
8 0.637019 11.2528 parabolic
9 0.637052 11.2528 parabolic
Optimization terminated:
the current x satisfies the termination criteria using OPTIONS.TolX of 1.000000e-04
x = 0.6370
Итеративный дисплей показывает текущее значение x и значение функции при f(x) каждый раз, когда происходит оценка функции. Для fminbnd, одна оценка функции соответствует одной итерации алгоритма. В последнем столбце показана процедура fminbnd использует в каждой итерации поиск золотого сечения или параболическую интерполяцию. Дополнительные сведения см. в разделе Итерационное отображение решателя оптимизации.
fminsearch функция аналогична fminbnd за исключением того, что он обрабатывает функции многих переменных. Укажите начальный вектор x0, а не начальный интервал. fminsearch пытается вернуть вектор x, который является локальным минимизатором математической функции вблизи этого начального вектора.
Попробовать fminsearch, создайте функцию three_var трех переменных, x, y, и z.
function b = three_var(v) x = v(1); y = v(2); z = v(3); b = x.^2 + 2.5*sin(y) - z^2*x^2*y^2;
Теперь найдите минимум для этой функции с помощью x = -0.6, y = -1.2, и z = 0.135 в качестве начальных значений.
v = [-0.6,-1.2,0.135];
a = fminsearch(@three_var,v)
a =
0.0000 -1.5708 0.1803 fminbnd и fminsearch решатели пытаются минимизировать объективную функцию. Если у вас проблема максимизации, то есть проблема формы
),
затем определяют g (x ) = -f (x) и минимизируют g.
Например, чтобы найти максимум загара (cos (x)) около x = 5, вычислите:
[x fval] = fminbnd(@(x)-tan(cos(x)),3,8)
x =
6.2832
fval =
-1.5574Максимум - 1,5574 (минус от сообщаемого fval) и происходит при x = 6,2832. Этот ответ верен, так как до пяти цифр максимум - tan (1 ) = 1.5574, что происходит при x = 2δ = 6.2832.
fminsearch Алгоритмfminsearch использует алгоритм симплекса Нелдера-Мид, как описано в Lagarias et al. [1]. Этот алгоритм использует симплекс из n + 1 точек для n-мерных векторов x. Алгоритм сначала делает симплекс вокруг начального предположения x0, добавляя 5% каждого компонента x0 (i) к x0. Алгоритм использует эти n векторов в качестве элементов симплекса в дополнение к x0. (Алгоритм использует 0,00025 в качестве компонента i, если x0 ( i) = 0.) Затем алгоритм многократно модифицирует симплекс в соответствии со следующей процедурой.
Примечание
Ключевые слова для fminsearch после описания шага отображается полужирным шрифтом.
Пусть x (i) обозначает список точек в текущем симплексе, i = 1,..., n + 1.
Упорядочивайте точки в симплексе от самого низкого значения функции f (x (1)) до самого высокого f (x (n + 1)). На каждом шаге итерации алгоритм отбрасывает текущую наихудшую точку x (n + 1) и принимает другую точку в симплекс. [Или, в случае шага 7 ниже, он изменяет все n точек со значениями выше f (x (1))].
Создание отраженной точки
| r = 2m - x (n + 1), | (1) |
где
| m = Startx (i )/n, i = 1... n, | (2) |
и вычисляют f (r).
Если f (x (1)) ≤ f (r) < f (x (n)), примите r и завершите эту итерацию. Размышлять
Если f (r) < f (x (1)), вычислите точку расширения s
| s = m + 2 (m - x (n + 1)), | (3) |
и вычислить f (s).
Если f (s) < f (r), примите s и завершите итерацию. Расшириться
В противном случае примите r и завершите итерацию. Размышлять
Если f (r) ≥ f (x (n)), выполните сжатие между m и eitherx (n + 1) или r, в зависимости от которого имеет более низкое значение целевой функции.
Если f (r) < f (x (n + 1)) (то есть r лучше x (n + 1)), вычислите
| c = m + (r - m )/2 | (4) |
и вычислить f (c). Если f ( c) < f (r), примите c и завершите итерацию. Договор вне
В противном случае перейдите к шагу 7 (Усадка).
Если f (r) ≥ f (x (n + 1)), вычислите
| cc = m + (x (n + 1) - m )/2 | (5) |
и вычислить f (cc). Если f ( cc) < f (x (n + 1)), примите cc и завершите итерацию. Договор внутри
В противном случае перейдите к шагу 7 (Усадка).
Вычислите n точек
| v (i) = x (1) + (x (i) - x (1) )/2 | (6) |
и вычисляют f (v (i)), i = 2,..., n + 1. Симплекс на следующей итерации - x (1), v (2),..., v (n + 1). Сжаться
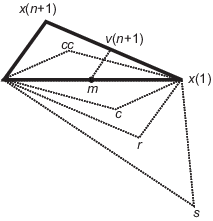
На следующем рисунке показаны точки, которые fminsearch может вычислить в процедуре вместе с каждым возможным новым симплексом. Исходный симплекс имеет жирный контур. Итерации продолжаются до тех пор, пока они не удовлетворяют критерию остановки.
[1] Лагариас, Дж. С., Дж. А. Ридс, М. Х. Райт и П. Э. Райт. «Свойства сходимости метода Nelder-Mead Simplex в малых размерах». Журнал оптимизации SIAM, том 9, номер 1, 1998, стр. 112-147.