CAGE можно использовать для создания таблицы подстановки, которая является обратной другой таблице подстановки. Инвертирование включает подстановку входных данных таблицы подстановки на выходные данные таблицы подстановки, и можно инвертировать 1-D или 2-D таблицы подстановки.
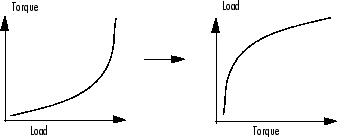
Инвертирование таблицы поиска позволяет связать стратегию вперед с стратегией назад; то есть замена входов и выходов. Этот процесс желателен, когда имеется стратегия «вперед», например, предсказание крутящего момента как функции скорости и нагрузки, и вы хотите изменить эту взаимосвязь в «стратегии назад», чтобы выяснить, какое значение нагрузки даст конкретный крутящий момент при определенной скорости.
Как правило, таблицы подстановки заполняются в CAGE путем сравнения с данными или моделями. В идеале вы хотите заполнить, используя правильную стратегию, но это может быть невозможно найти или измерить. Если имеется только перспективная стратегия, но требуется обратная стратегия, можно заполнить с помощью форвардной стратегии (таблицы или модели), а затем инвертировать таблицу поиска.
Например, для заполнения таблицы поиска, как правило, из модели, необходимо, чтобы отклик модели был выводом таблицы поиска, а входные данные модели - функцией входных данных таблицы поиска (или должна быть возможность получения входных данных, например, массы воздуха из давления в коллекторе). Если доступная модель является «инвертированной» (отклик модели является вводом таблицы подстановки, а вывод таблицы подстановки является вводом модели) и изменить модель невозможно, таблицу подстановки можно инвертировать в CAGE.
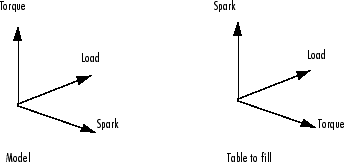
На схеме приведенной таблицы поиска оси x и y представляют нормализаторы (которые должны быть искрой и нагрузкой), а ось z является выходным сигналом в каждой точке останова (крутящий момент). Правильное заполнение таблицы подстановки из модели является двухэтапным процессом. Сначала заполните таблицу подстановки, которая имеет те же входные и выходные данные, что и модель, а затем заполните вторую таблицу подстановки путем инверсии.
Чтобы инверсия была детерминированной и точной, таблица поиска, подлежащая инвертированию, должна быть монотонной; то есть всегда увеличивается или уменьшается. Это требование аналогично одномерному примеру. Каждая точка на оси Y должна соответствовать уникальной точке на оси X. Та же проблема относится и к двумерным таблицам подстановки: для любого заданного вывода в первой таблице подстановки должно быть уникальное условие ввода; то есть каждая точка на оси z должна соответствовать уникальной точке в плоскости x-y. Некоторые инверсии таблицы подстановки имеют несколько значений и поэтому не удовлетворяют этому требованию, так же как функция квадратного корня может принимать либо положительные, либо отрицательные значения. Для решения этой проблемы можно использовать мастер инверсии CAGE; можно управлять процессом инверсии и определять, что делать в этих случаях.
Следующий пример иллюстрирует таблицу подстановки с несколькими значениями. Существует два решения для одного значения крутящего момента. CAGE имеет средство инверсии таблицы поиска, которое может помочь в решении этой проблемы. Можно указать, следует ли использовать верхние или нижние значения для заполнения определенных частей таблицы подстановки; это позволяет успешно инвертировать функцию с несколькими значениями. См. инструкции по инверсии для таблиц поиска 1-D и 2-D в следующих разделах.
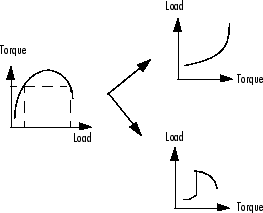
Процесс инвертирования одномерной таблицы поиска отличается от процесса инвертирования двумерной таблицы поиска.
Чтобы инвертировать одномерную таблицу поиска,
Убедитесь, что сеанс содержит две таблицы подстановки:
Первая таблица поиска 1D, которую требуется инвертировать, заполнена.
Другая 1D таблица подстановки с другим вводом, которую необходимо заполнить инвертированной таблицей подстановки.
Выделите таблицу подстановки, которую требуется инвертировать.
Щелкните![]() или выберите Таблица (Table) > Инвертировать (Invert).
или выберите Таблица (Table) > Инвертировать (Invert).
Откроется диалоговое окно Инверсия таблицы (Table Inversion).
CAGE выбирает подходящую таблицу в списке «Таблица для заполнения». Убедитесь, что это таблица подстановки, которую необходимо заполнить, или выберите другую.
Следующий элемент управления, Resolve non unique inverses with, указывает, что CAGE должен делать, если он встречает несколько значений. Чтобы минимизировать ошибку, оставьте значение по умолчанию, Least squares. Возможны следующие варианты:
Least squares выбирает диапазон, который приводит к наименьшей ошибке (см. ниже; последняя страница мастера отображает метрику ошибки).
Minimum выбирает нижний из двух, если данное число имеет два возможных обратного (например, выбор отрицательного квадратного корня числа).
Maximum выбирает самый верхний диапазон, если данное число имеет два возможных обратного (например, выбор положительного квадратного корня числа).
Intermediate выбирает средний диапазон, если заданное число имеет более двух возможных обратных значений.
Например, функцию y = x2 невозможно инвертировать в диапазоне от -1 до 1. Можно задать инвертирование диапазона от 0 до 1, жертвуя инверсией в нижнем диапазоне или в обратном. Чтобы выбрать диапазон от 0 до 1, выделитеMaximum.
На дисплее отображается сравнение между таблицей поиска (зеленым цветом) и функцией x = f-1 (f (x)).
Нижняя панель диалогового окна имеет график, отображающий ошибку инверсии. При необходимости можно изменить тип графика на «Ввод» и «Вывод». Если ваша прямая функция y = f (x), и ваша обратная функция x = g (y), то, объединяя их, в идеальном мире, вы должны иметь x = g (f (x)). Затем график отображает линию, показывающую x против x, и линию, показывающую x против g (f (x)). Близость этих двух линий указывает на то, насколько хороша была инверсия: совершенная инверсия показывает линии точно поверх друг друга.
График может показать, какая часть таблицы поиска не была успешно инвертирована и где следует попробовать другую процедуру.
Примечание
Процедура инверсии наименьших квадратов пытается минимизировать общее расстояние между этими линиями. Иногда это может привести к неожиданным результатам. Например, если задана функция f (x) = x ^ 2 от -1 до 1, то если в качестве обратного выбран положительный или отрицательный квадратный корень, это вызывает большую ошибку в объединенном обратном. Если выбрать g (y) = sqrt (y), то g (f (-1)) = 1, ошибка 2. Чтобы минимизировать это, процедура наименьших квадратов может выбрать отправку всего в ноль и принятие средней ошибки по всему диапазону, а не большой ошибки по половине диапазона. Используйте знания о форме таблицы поиска, которую вы инвертируете, чтобы помочь выбрать подпрограмму для выбора.
Нажмите кнопку ОК, чтобы принять инверсию, или кнопку Отмена, чтобы проигнорировать результат и вернуться к исходной таблице подстановки.
Чтобы инвертировать двумерную таблицу поиска,
Убедитесь, что сеанс содержит две таблицы подстановки:
Первая таблица подстановки, которую требуется инвертировать.
Вторая таблица подстановки с одним и тем же вводом, который требуется заполнить инвертированной таблицей подстановки.
Выделите таблицу подстановки, которую требуется инвертировать.
Щелкните![]() или выберите Таблица (Table) > Инвертировать (Invert).
или выберите Таблица (Table) > Инвертировать (Invert).
Откроется диалоговое окно Инверсия таблицы (Table Inversion).
CAGE выбирает подходящую таблицу в списке «Таблица для заполнения». Убедитесь, что это таблица, которую вы хотите заполнить, или выберите другую.
Следующий элемент управления, Resolve non unique inverses with, указывает, что CAGE должен делать, если он встречает несколько значений. Чтобы минимизировать ошибку, оставьте значение по умолчанию, Least squares. Другие опции см. в разделе инвертирование таблицы 1D.
Нижняя панель диалогового окна имеет график, отображающий ошибку инверсии. При необходимости можно изменить тип графика для просмотра параметров «Ввод» и «Вывод». Если прямой функцией является z = f (x, y), а обратной функцией является x = g (y, z), то, объединяя их, в идеальном мире следует иметь x = g (y, f (x, y)). Затем график отображает плоскость, показывающую x, нанесенную на график относительно x и y, и цветную поверхность, показывающую g (y, f (x, y)), нанесенную на график относительно x и y. Близость этих двух плоскостей показывает, насколько хороша инверсия. Чтобы улучшить инверсию в некоторых областях, попробуйте другие параметры в разделе Разрешить неуникальные инверсии в.
Нажмите кнопку ОК, чтобы принять результат, или кнопку Отмена, чтобы проигнорировать результат и вернуться к исходной таблице.