Расчетный контроллер ПДК для позиционного сервомеханизма

В этом примере показано, как с помощью MPC Designer сконструировать контроллер прогнозирования модели для сервомеханизма положения.

Модель системы

Позиционный сервомеханизм состоит из двигателя постоянного тока, коробки передач, упругого вала и нагрузки.

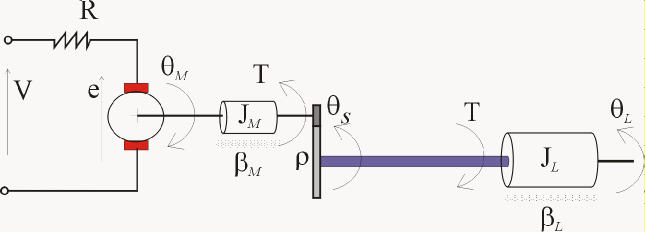
Дифференциальные уравнения, представляющие эту систему:

$\begin{array}{l} {\overset{}{}}_{} \frac{_{}}{_{ωШL =−kTJL}}_{} \frac{_{}}{} \frac{_{}}{_{}}_{} \\ {\overset{}{}}_{} \frac{_{}}{_{}} \frac{(θL−θMρ) −βLJLωLω˙M=kMJM_{}_{}}{} \frac{_{}_{}}{_{}} \frac{_{}}{_{}}_{} (V-kMωMR) -βMωMJM+kTρJM \frac{_{}}{} \end{array}$ (θL−θMρ)

где,

V - приложенное напряжение.
T - крутящий момент, воздействующий на нагрузку.
$_{} {\overset{}{}}_{ωL=θ˙L}$ - угловая скорость нагрузки.
$_{} {\overset{}{}}_{ωM=θ˙M}$ - угловая скорость вала двигателя.

Остальные члены являются постоянными параметрами.

Постоянные параметры для модели сервомеханизма

Символ	Значение (единицы СИ)	Определение
_kT	1280.2	Жесткость на кручение
_км	10	Постоянная двигателя
_JM	0.5	Инерция двигателя
_JL	_50JM	Инерция нагрузки
ρ	20	Передаточное число
_βM	0.1	Коэффициент трения по вязкости двигателя
_βL	25	Коэффициент вязкого трения нагрузки
R	20	Сопротивление якоря

Если определить переменные состояния как

$_{xp} = {\begin{matrix} _{} & _{} & _{} & _{[θLωLθMωM} \end{matrix}]}^{T},$

затем можно смоделировать сервомеханизм как систему состояния-пространства LTI.

$\begin{matrix} {\overset{}{}}_{x˙p} = \begin{matrix} \frac{_{}}{_{}} & \frac{_{}}{_{}} & \frac{_{}}{_{}} \\ \frac{_{}}{_{}} & \frac{_{}}{^{}_{}} & \frac{_{} \frac{_{}^{}}{}}{_{}} \end{matrix}_{[0100−kTJL−βLJLkTρJL00001kTρJM0−kTρ2JM−βM+kM2RJM]xp} + \begin{matrix} \frac{_{}}{_{}} \end{matrix} \\ _{[000kMRJM]VθL} = \begin{matrix} \end{matrix} [1000]_{} \\ xpT = \begin{matrix} _{} & \frac{_{}}{} \end{matrix}_{[kT0−kTρ0]xp} \end{matrix}$

Контроллер должен установить угловое положение нагрузки, (, _В), на требуемое значение, регулируя приложенное напряжение, В.

Однако, поскольку эластичный вал имеет конечную прочность на сдвиг, крутящий момент T должен находиться в диапазоне | T | ≤ 78,5 Нм. Кроме того, источник напряжения физически ограничивает приложенное напряжение диапазоном | В | ≤ 220 В.

Создание модели завода

Укажите константы модели.

Kt = 1280.2;  % Torsional rigidity
Km = 10;      % Motor constant
Jm = 0.5;     % Motor inertia
Jl = 50*Jm;   % Load inertia
N = 20;       % Gear ratio
Bm = 0.1;     % Rotor viscous friction
Bl = 25;      % Load viscous friction
R = 20;       % Armature resistance

Определите матрицы состояния-пространства, полученные из уравнений модели.

A = [        0       1             0                0;
        -Kt/Jl  -Bl/Jl     Kt/(N*Jl)                0;
             0       0             0                1;
     Kt/(Jm*N)       0  -Kt/(Jm*N^2)  -(Bm+Km^2/R)/Jm];
B = [0; 0; 0; Km/(R*Jm)];
C = [  1  0       0  0;
      Kt  0   -Kt/N  0];
D = [0; 0];

Создание модели пространства состояний.

plant = ss(A,B,C,D);

Открыть приложение MPC Designer

mpcDesigner

Импорт оборудования и определение конфигурации сигналов

В MPC Designer на вкладке MPC Designer выберите MPC Structure.

В диалоговом окне «Определение структуры MPC путем импорта» выберите plant модель установки и назначить каналы ввода/вывода установки следующим типам сигналов:

Управляемая переменная - напряжение, В
Измеренный выходной сигнал - Угловое положение нагрузки, _startL
Неизмеренный выход - крутящий момент, Т

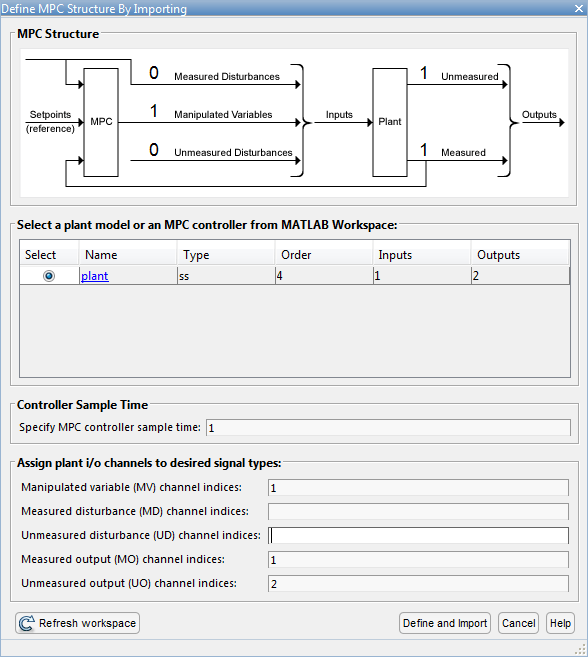
Щелкните Определить (Define) и Импортировать (Import).

MPC Designer импортирует указанное производство в браузер данных. Кроме того, в обозреватель данных добавляются следующие элементы:

mpc1 - Контроллер MPC по умолчанию, созданный с помощью plant в качестве внутренней модели.
scenario1 - Сценарий моделирования по умолчанию. Результаты этого моделирования отображаются на графиках «Входной ответ» и «Выходной ответ».

Определение атрибутов канала ввода и вывода

На вкладке Конструктор MPC (MPC Designer) в разделе Структура (Structure) щелкните Атрибуты ввода-вывода (I/O Attributes).

В диалоговом окне «Характеристики канала ввода и вывода» для каждого канала ввода и вывода:

Укажите значимое имя и единицу измерения.
Сохранить номинальное значение по умолчанию, равное 0.

Укажите масштабный коэффициент для нормализации сигнала. Выберите значение, аппроксимирующее прогнозируемый рабочий диапазон сигнала:

Название канала	Минимальное значение	Максимальное значение	Масштабный коэффициент
`Voltage`	-220 В	220 В	`440`
`Theta`	-δ радиан	δ радиан	`6.28`
`Torque`	-78,5 Нм	78,5 Нм	`157`

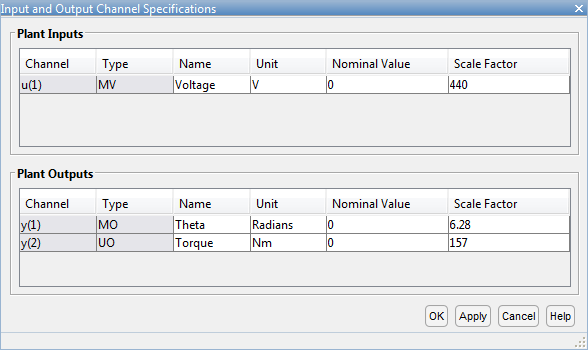
Нажмите кнопку ОК, чтобы обновить атрибуты канала и закрыть диалоговое окно.

Изменение сценария для моделирования ответа шага углового положения

В разделе Сценарий в раскрывающемся списке Изменить сценарий выберите scenario1 для изменения сценария моделирования по умолчанию.

В диалоговом окне «Сценарий моделирования» задайте продолжительность моделирования, равную 10 секунд.

В таблице Опорные сигналы сохраните конфигурацию по умолчанию для первого канала. Эти параметры создают Step изменение 1 радиан в уставке углового положения в момент времени 1 второй.

Для второго выхода в выпадающем списке Signal выберите Constant для поддержания уставки крутящего момента на номинальном уровне.

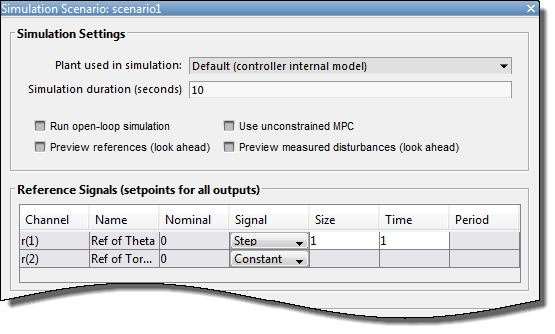
Нажмите кнопку ОК.

Приложение запускает моделирование с новыми настройками сценария и обновляет графики «Входной ответ» и «Выходной ответ».

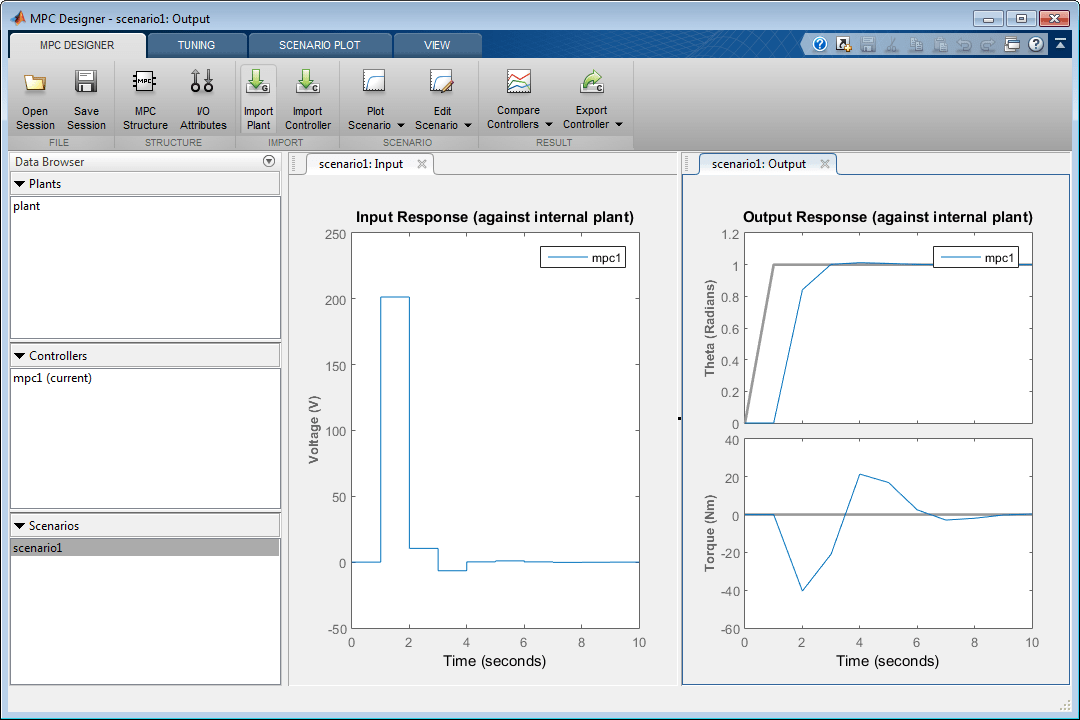
Определение времени и горизонтов выборки контроллера

На вкладке Настройка в разделе Горизонт укажите время образца 0.1 секунд.

Для заданного времени выборки _Ts и требуемого времени отклика _Tr = 2 секунды выберите горизонт прогнозирования p, который:

$_{}_{Tr≈pTs} .$

Поэтому укажите горизонт прогнозирования 20.

Укажите горизонт управления 5.

При обновлении значений времени выборки и горизонта графики «Ответ на ввод» и «Ответ на вывод» обновляются автоматически. Значения входного напряжения и крутящего момента превышают ограничения, определенные в спецификациях модели системы.

Задать зависимости

В разделе «Проектирование» выберите «Зависимости».

В диалоговом окне Зависимости (Constraints) в разделе Ограничения ввода (Input Constraints) задайте значения минимального и максимального напряжения для управляемой переменной (MV).

В разделе Ограничения вывода (Output Constraints) задайте значения минимального и максимального крутящего момента для неизмеренного выходного сигнала (UO).

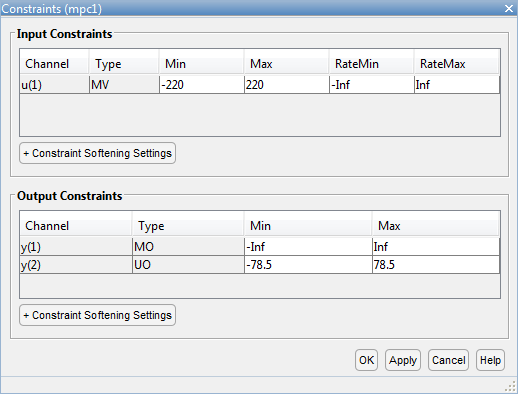
Дополнительные ограничения отсутствуют, то есть остальные ограничения остаются на максимальных и минимальных значениях по умолчанию. —Inf и Inf соответственно

Нажмите кнопку ОК.

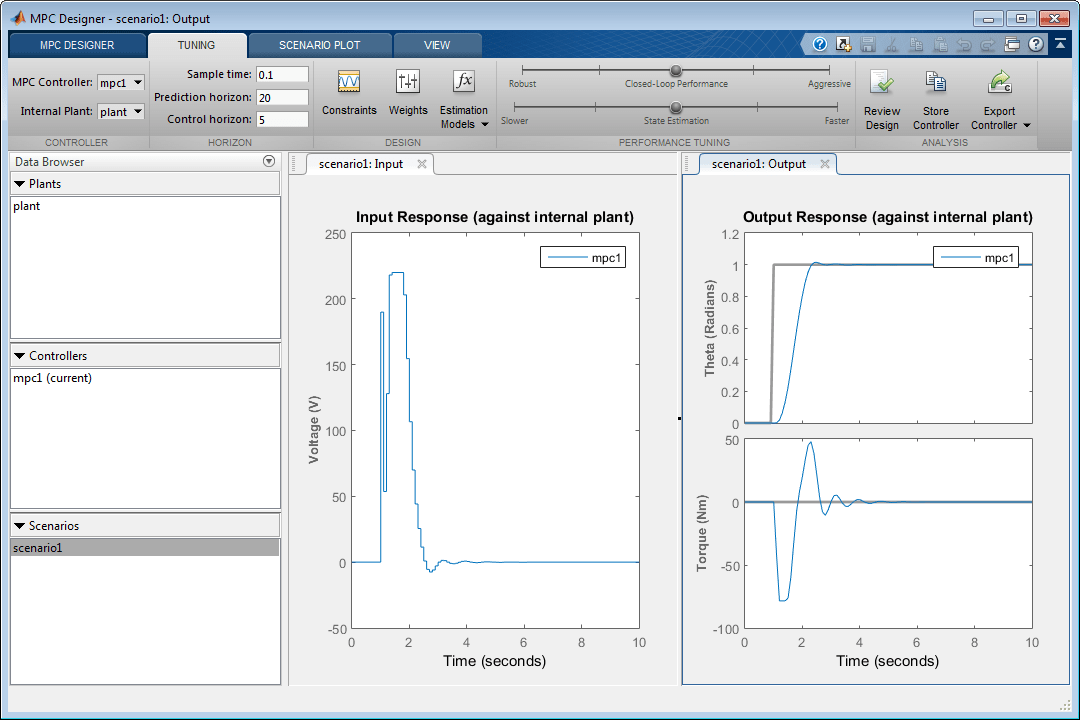
Графики ответа обновляются для отражения новых ограничений. На графике «Входной отклик» имеются нежелательные большие изменения входного напряжения.

Задание веса настройки

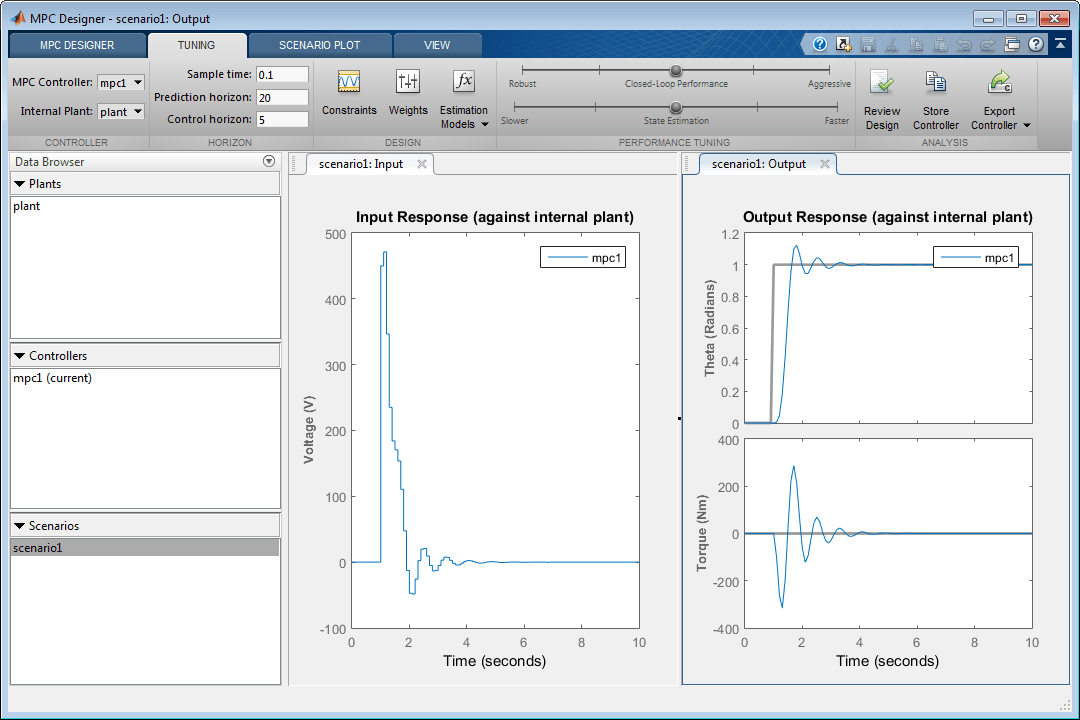
В разделе «Проектирование» выберите «Веса».

В диалоговом окне Веса (Weights) в таблице Входные веса (Input Weights) увеличьте управляемую переменную Вес скорости (Rate Weight).

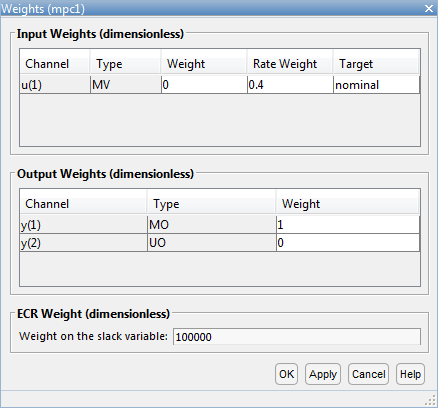
Вес настройки для управляемой переменной (MV) равен 0. Этот вес указывает на то, что контроллер может допускать изменение входного напряжения в пределах ограниченного диапазона. Увеличенный вес скорости ограничивает размер изменяемых переменных.

Поскольку целью управления является угловое положение нагрузки для отслеживания ее уставки, вес настройки на измеренном выходе равен 1. Отсутствует уставка для приложенного крутящего момента, поэтому контроллер может позволить второму выходному сигналу изменяться в пределах своих ограничений. Поэтому вес неизмеренного выходного сигнала (UO) равен 0, что позволяет контроллеру игнорировать уставку крутящего момента.

Нажмите кнопку ОК.

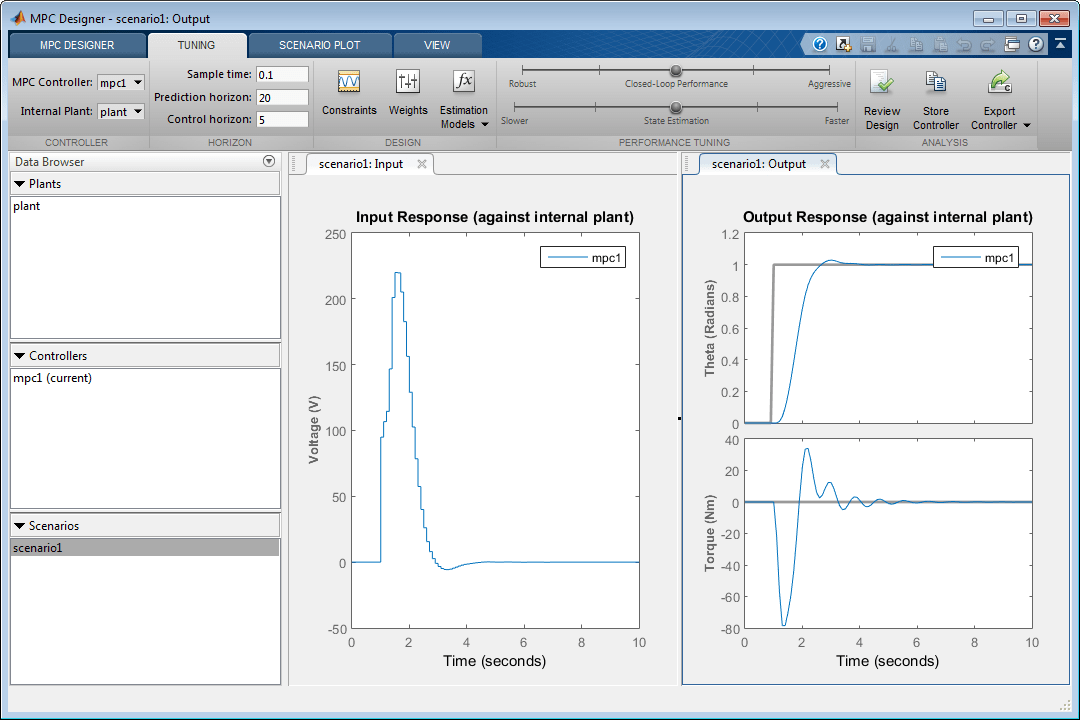
График ответа обновляется для отражения увеличенного веса скорости. Входной отклик является более плавным с меньшими изменениями напряжения.

Проверить выходной отклик

На графике «Ответ на вывод» щелкните правой кнопкой мыши область графика «Тета» и выберите «Характеристики» > «Ответ на пик».

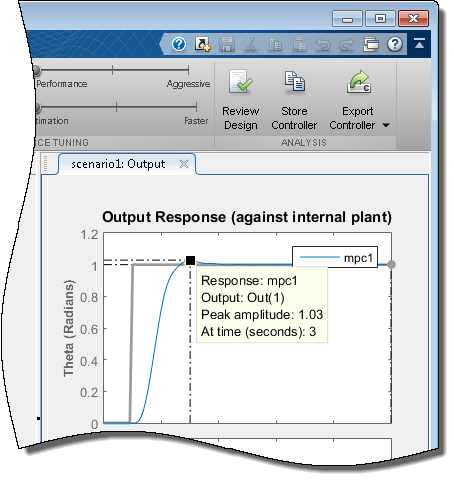
Пиковый выходной отклик возникает во время 3 секунд при максимальном превышении 3%. Поскольку изменение шага опорного сигнала составляет 1 секунду, контроллер имеет время пика 2 секунды.

Увеличение времени отклика контроллера

Щелкните и перетащите ползунок Производительность замкнутого цикла вправо, чтобы получить более агрессивный ответ. Чем дальше вы перетаскиваете ползунок вправо, тем быстрее реагирует контроллер. Выберите положение ползунка таким образом, чтобы пиковый отклик приходился на 2,7 секунды.

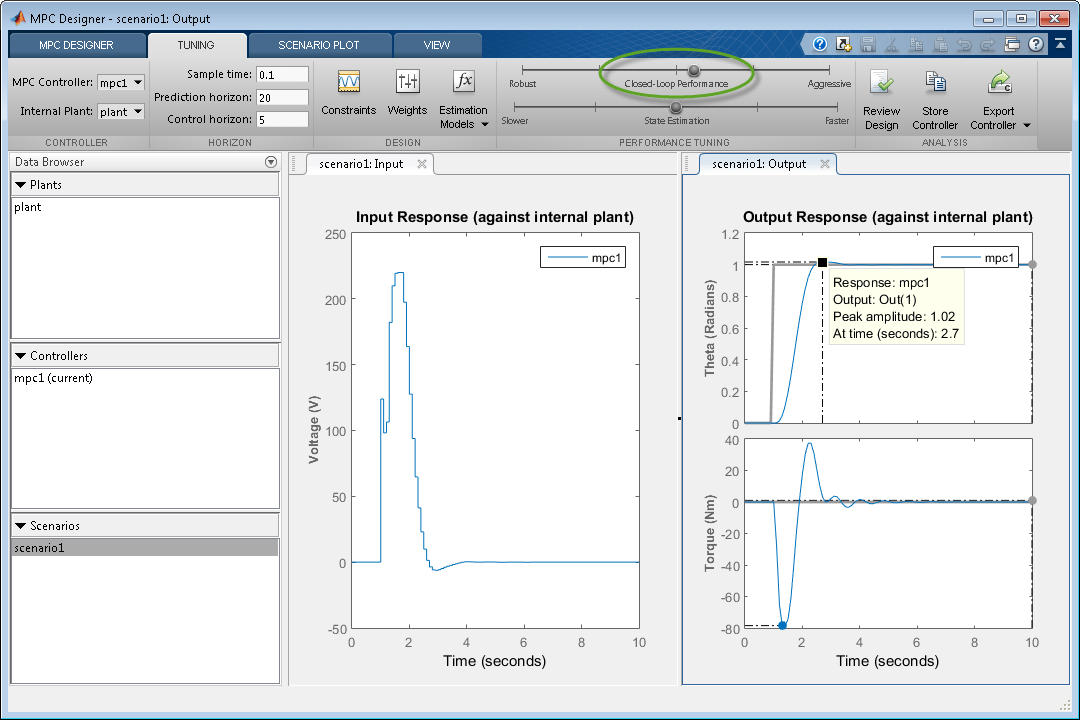
Конечное пиковое время контроллера составляет 1,7 секунды. Уменьшение времени отклика дополнительно приводит к чрезмерно агрессивным изменениям входного напряжения.

Создание и выполнение сценария MATLAB

В разделе Анализ (Analysis) щелкните стрелку Контроллер экспорта (Export Controller).

В разделе Контроллер экспорта (Export Controller) щелкните Generate Script.

В диалоговом окне «Создание сценария MATLAB ®» установите флажок рядом со значкомscenario1.

Щелкните Создать сценарий (Generate Script).

Приложение экспортирует копию модели завода, plant_C, в рабочее пространство MATLAB вместе с моделирующими входными и опорными сигналами.

Кроме того, приложение генерирует следующий код в редакторе MATLAB.

%% create MPC controller object with sample time
mpc1 = mpc(plant_C, 0.1);
%% specify prediction horizon
mpc1.PredictionHorizon = 20;
%% specify control horizon
mpc1.ControlHorizon = 5;
%% specify nominal values for inputs and outputs
mpc1.Model.Nominal.U = 0;
mpc1.Model.Nominal.Y = [0;0];
%% specify scale factors for inputs and outputs
mpc1.MV(1).ScaleFactor = 440;
mpc1.OV(1).ScaleFactor = 6.28;
mpc1.OV(2).ScaleFactor = 157;
%% specify constraints for MV and MV Rate
mpc1.MV(1).Min = -220;
mpc1.MV(1).Max = 220;
%% specify constraints for OV
mpc1.OV(2).Min = -78.5;
mpc1.OV(2).Max = 78.5;
%% specify overall adjustment factor applied to weights
beta = 1.2712;
%% specify weights
mpc1.Weights.MV = 0*beta;
mpc1.Weights.MVRate = 0.4/beta;
mpc1.Weights.OV = [1 0]*beta;
mpc1.Weights.ECR = 100000;
%% specify simulation options
options = mpcsimopt();
options.RefLookAhead = 'off';
options.MDLookAhead = 'off';
options.Constraints = 'on';
options.OpenLoop = 'off';
%% run simulation
sim(mpc1, 101, mpc1_RefSignal, mpc1_MDSignal, options);

В окне MATLAB на вкладке Редактор выберите Сохранить.

Заполните диалоговое окно Сохранить и нажмите кнопку Сохранить.

На вкладке «Редактор» нажмите «Выполнить».

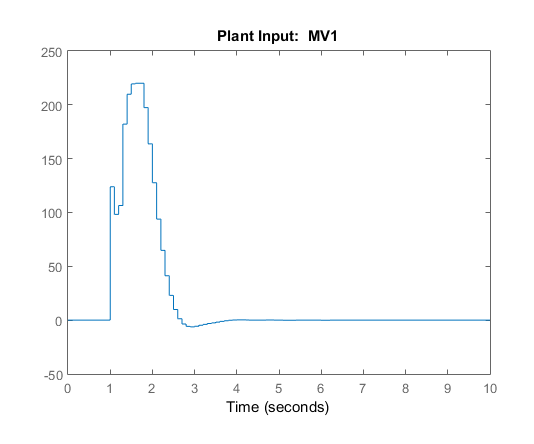
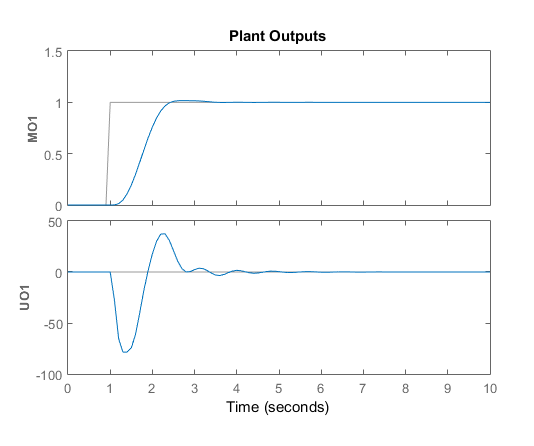
Сценарий создает контроллер, mpc1и запускает сценарий моделирования. Входные и выходные ответы соответствуют результатам моделирования из приложения.

Проверка производительности контроллера в Simulink

При наличии модели системы Simulink ® можно смоделировать контроллер и проверить его производительность. Функции Simulink не поддерживаются в MATLAB Online™.

Откройте модель.

open_system('mpc_motor')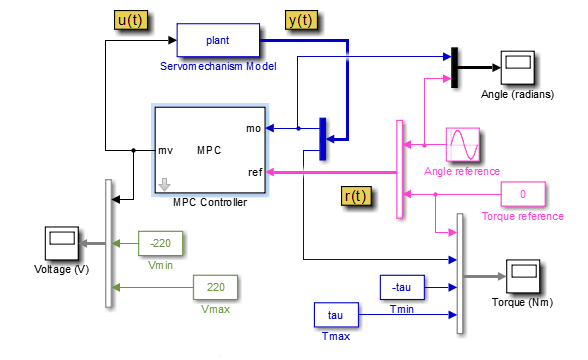

Эта модель использует блок контроллера MPC для управления установкой сервомеханизма. Блок модели сервомеханизма уже настроен для использования plant из рабочей области MATLAB.

Блок опорного источника угла создает синусоидальный опорный сигнал с частотой 0.4 rad/sec и амплитуда δ.

Дважды щелкните блок контроллера MPC.

В диалоговом окне «Параметры блока контроллера MPC» укажите контроллер MPC в рабочей области MATLAB. Используйте mpc1 контроллер, созданный с помощью созданного сценария.

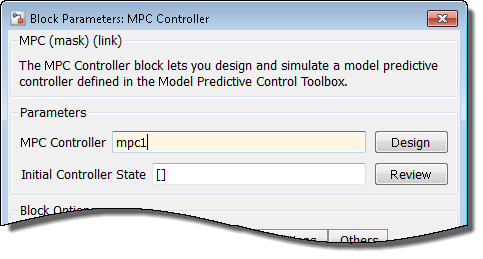
Нажмите кнопку ОК.

В командной строке MATLAB укажите переменную зависимости величины крутящего момента.

tau = 78.5;

Модель использует это значение для построения графика ограничений для области вывода крутящего момента.

В окне Модель симуляции (Simulink model) щелкните Выполнить (Run), чтобы смоделировать модель.

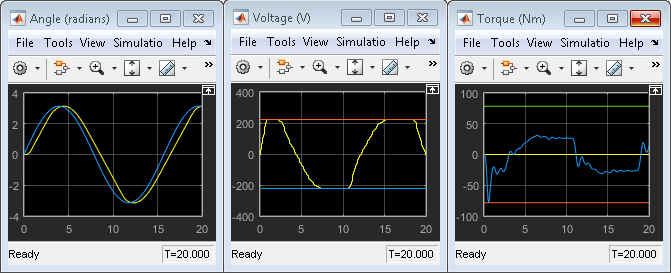
В области Угол выходной отклик, желтый, отслеживает уставку углового положения, синий, близко.

См. также

mpc | Контроллер MPC | Разработчик MPC

Документация