Ориентация по показаниям магнитометра и акселерометра
orientation = ecompass(accelerometerReading,magnetometerReading)quaternion которые могут поворачивать величины из родительского (NED) кадра в дочерний (сенсорный) кадр.
orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat)quaternion или матрица вращения.
orientation = ecompass(accelerometerReading,magnetometerReading,orientationFormat,'ReferenceFrame',RF)RF из orientation выход. Определить RF как 'NED' (Север-Восток-вниз) или 'ENU' (Восток-Север-Вверх). Значение по умолчанию: 'NED'.
Используйте известную напряженность магнитного поля и правильное ускорение устройства, направленного на север в Бостоне, чтобы определить магнитное склонение Бостона.
Определите известное ускорение и напряженность магнитного поля в Бостоне.
magneticFieldStrength = [19.535 -5.109 47.930]; properAcceleration = [0 0 9.8];
Передать напряженность и ускорение магнитного поля в ecompass функция. ecompass функция возвращает оператор вращения кватерниона. Преобразуйте кватернион в углы Эйлера в градусах.
q = ecompass(properAcceleration,magneticFieldStrength); e = eulerd(q,'ZYX','frame');
Угол, e, представляет угол между истинным севером и магнитным севером в Бостоне. По условию, магнитное склонение является отрицательным, когда магнитный север находится к западу от истинного севера.
magneticDeclinationOfBoston = -e(1)
magneticDeclinationOfBoston = -14.6563
ecompass функция объединяет данные магнитометра и акселерометра для возврата кватерниона, который при использовании в операторе вращения кватерниона может поворачивать величины из родительского (NED) кадра в дочерний кадр. ecompass функция может также возвращать матрицы вращения, которые выполняют эквивалентные вращения в качестве оператора кватерниона.
Определите поворот, который может принимать родительский кадр, указывающий на магнитный север, к дочернему кадру, указывающему на географический север. Определите поворот как кватернион и матрицу вращения. Затем преобразуйте матрицу кватерниона и поворота в углы Эйлера в градусах для сравнения.
Определите напряженность магнитного поля в микротеслах в Бостоне, штат Массачусетс, если указать истинный север.
m = [19.535 -5.109 47.930]; a = [0 0 9.8];
Определите матрицу кватерниона и вращения, которая способна поворачивать кадр с магнитного севера на истинный север.
q = ecompass(a,m); quaterionEulerAngles = eulerd(q,'ZYX','frame')
quaterionEulerAngles = 1×3
14.6563 0 0
r = ecompass(a,m,'rotmat');
theta = -asin(r(1,3));
psi = atan2(r(2,3)/cos(theta),r(3,3)/cos(theta));
rho = atan2(r(1,2)/cos(theta),r(1,1)/cos(theta));
rotmatEulerAngles = rad2deg([rho,theta,psi])rotmatEulerAngles = 1×3
14.6563 0 0
Использовать ecompass для определения вектора гравитации на основе данных вращающегося IMU.
Загрузите данные блока инерциальных измерений (IMU).
load 'rpy_9axis.mat' sensorData Fs
Определите ориентацию корпуса датчика относительно локального кадра NED с течением времени.
orientation = ecompass(sensorData.Acceleration,sensorData.MagneticField);
Чтобы оценить вектор силы тяжести, сначала поверните показания акселерометра из корпуса датчика в корпус NED с помощью orientation вектор кватерниона.
gravityVectors = rotatepoint(orientation,sensorData.Acceleration);
Определите вектор гравитации как среднее значение восстановленных векторов гравитации с течением времени.
gravityVectorEstimate = mean(gravityVectors,1)
gravityVectorEstimate = 1×3
0.0000 -0.0000 10.2102
Запал смоделированных данных акселерометра и гироскопа для отслеживания вращающейся платформы с использованием идеализированных и реалистичных данных.
Создание траектории «земля-истина»
Опишите ориентацию платформы с течением времени. Используйте kinematicTrajectory Система object™, чтобы создать траекторию для платформы, которая не имеет поступательного движения и вращений вокруг своей оси Z.
duration = 12;
fs = 100;
numSamples = fs*duration;
accelerationBody = zeros(numSamples,3);
angularVelocityBody = zeros(numSamples,3);
zAxisAngularVelocity = [linspace(0,4*pi,4*fs),4*pi*ones(1,4*fs),linspace(4*pi,0,4*fs)]';
angularVelocityBody(:,3) = zAxisAngularVelocity;
trajectory = kinematicTrajectory('SampleRate',fs);
[~,orientationNED,~,accelerationNED,angularVelocityNED] = trajectory(accelerationBody,angularVelocityBody);Модель, получающая данные IMU
Использовать imuSensor Система предназначена для имитации данных, полученных от IMU, который содержит идеальный магнитометр и идеальный акселерометр.
IMU = imuSensor('accel-mag','SampleRate',fs); [accelerometerData,magnetometerData] = IMU(accelerationNED, ... angularVelocityNED, ... orientationNED);
Плавкий предохранитель IMU для оценки ориентации
Передача данных акселерометра и магнитометра в ecompass функция оценки ориентации во времени. Преобразуйте ориентацию в углы Эйлера в градусах и постройте график результата.
orientation = ecompass(accelerometerData,magnetometerData); orientationEuler = eulerd(orientation,'ZYX','frame'); timeVector = (0:numSamples-1).'/fs; figure(1) plot(timeVector,orientationEuler) legend('z-axis','y-axis','x-axis') xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation from Ideal IMU')
Повторить эксперимент с реалистичной моделью датчика IMU
Изменение параметров IMU Объект системы для аппроксимации реалистичных данных датчика IMU. Сбросить IMU и затем назовите его с тем же ускорением «земля-истина», угловой скоростью и ориентацией. Использовать ecompass чтобы сплавить данные IMU и построить график результатов.
IMU.Accelerometer = accelparams( ... 'MeasurementRange',20, ... 'Resolution',0.0006, ... 'ConstantBias',0.5, ... 'AxesMisalignment',2, ... 'NoiseDensity',0.004, ... 'BiasInstability',0.5); IMU.Magnetometer = magparams( ... 'MeasurementRange',200, ... 'Resolution',0.01); reset(IMU) [accelerometerData,magnetometerData] = IMU(accelerationNED,angularVelocityNED,orientationNED); orientation = ecompass(accelerometerData,magnetometerData); orientationEuler = eulerd(orientation,'ZYX','frame'); figure(2) plot(timeVector,orientationEuler) legend('z-axis','y-axis','x-axis') xlabel('Time (s)') ylabel('Rotation (degrees)') title('Orientation from Realistic IMU')
ecompass функция возвращает матрицу кватерниона или поворота, которая может поворачивать величины из родительского (NED, например) кадра в дочерний (сенсорный) кадр. Для обоих форматов ориентации вывода оператор поворота определяется вычислением матрицы поворота.
Матрицу вращения сначала вычисляют с помощью промежуточного средства:
aa × ma]
и затем нормализовано по столбцам. a и m являются accelerometerReading входные данные и magnetometerReading вход, соответственно.
Чтобы понять вычисление матрицы вращения, рассмотрим произвольную точку на Земле и соответствующий ей локальный кадр NED. Предположим, что корпус датчика [x, y, z] имеет то же начало координат.
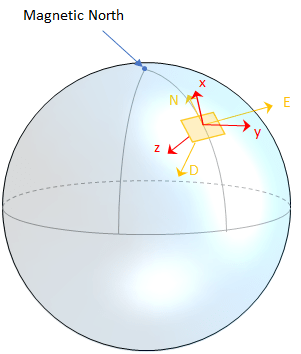
Напомним, что ориентация корпуса датчика определяется как оператор поворота (матрица поворота или кватернион), необходимый для поворота величины от родительского (NED) кадра к дочернему (корпусу датчика) кадру:
pchild]
где
R - матрица вращения 3 на 3, которая может быть интерпретирована как ориентация дочернего кадра.
pparent является вектором 3 на 1 в родительском кадре.
pchild - вектор 3 на 1 в дочернем кадре.
Для стабильного корпуса датчика акселерометр возвращает ускорение под действием силы тяжести. Если корпус датчика полностью выровнен с системой координат NED, все ускорение, вызванное гравитацией, происходит вдоль оси Z, и акселерометр считывает [0 0 1]. Рассмотрим матрицу вращения, необходимую для поворота величины от системы координат NED до величины, указанной акселерометром.
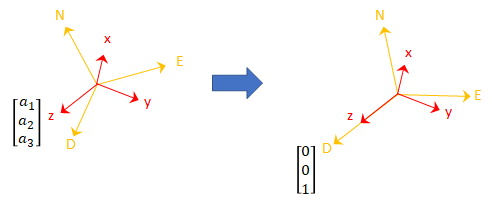
Третий столбец матрицы вращения соответствует показанию акселерометра:
Магнитометр, считывающий данные, указывает на магнитный север и находится в плоскости N-D. Рассмотрим корпус датчика, выровненный с системой координат NED.
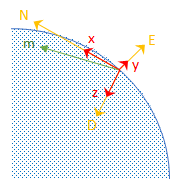
По определению, ось E перпендикулярна плоскости N-D, поэтому N ⨯ D = E, в пределах некоторого масштабирования амплитуды. Если корпус датчика совмещен с NED, то вектор ускорения от акселерометра и вектор магнитного поля от магнитометра лежат в плоскости N-D. Поэтому m ⨯ a = y, снова с некоторым масштабированием амплитуды.
Рассмотрим матрицу поворота, необходимую для поворота NED к дочернему кадру, [x y z].
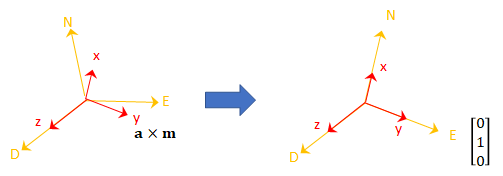
Второй столбец матрицы вращения соответствует поперечному произведению показаний акселерометра и магнитометра:
По определению матрицы вращения столбец 1 является перекрестным произведением столбцов 2 и 3:
m) × a
Наконец, матрица вращения нормализуется по столбцам:
Примечание
ecompass алгоритм использует для системы координат NED магнитный север, а не истинный север.
[1] Слияние датчиков с открытым исходным кодом. https://github.com/memsindustrygroup/Open-Source-Sensor-Fusion/tree/master/docs