Дифференциальное уравнение в частных производных Toolbox™ использует сети с треугольными элементами для 2-D геометрий, а сети с тетраэдрическими элементами для 3-D геометрий. В более ранних версиях панели инструментов дифференциальных уравнений в частных производных используются сетки в виде [p,e,t] тройной. Матрицы p, e, и t представляют точки (узлы), элементы и треугольники или тетраэдры сетки соответственно. Более поздние версии панели инструментов поддерживают [p,e,t] сетки из соображений совместимости.
Примечание
Новые возможности могут быть несовместимы с устаревшим рабочим процессом. Описание данных сетки в рекомендуемом рабочем процессе см. в разделе Данные сетки.
Данные сетки для 2-D сетки имеют следующие компоненты:
p (точки, узлы сетки) 2около-Np матрица узлов, где Np - количество узлов в сетке. Каждый столбец p(:,k) состоит из x-координаты точки k в p(1,k) и координата точки по оси Y k в p(2,k).
e (рёбра) является 7около-Ne матрица рёбер, где Ne - количество кромок в сетке. Кромки сети в e и края геометрии имеют соответствие один к одному. e матрица представляет дискретные кромки геометрии таким же образом, как t матрица представляет дискретные грани. Каждый столбец в e матрица представляет одно ребро.
e(1,k) - индекс первой точки кромки сетки k.
e(2,k) - индекс второй точки в ребре сетки k.
e(3,k) - значение параметра в первой точке кромки k. Значение параметра связано с длиной дуги вдоль геометрической кромки.
e(4,k) - значение параметра во второй точке кромки k.
e(5,k) - идентификатор геометрической кромки, содержащей кромку сети. Идентификаторы кромок можно просмотреть с помощью команды pdegplot(geom,'EdgeLabels','on').
e(6,k) - номер поддомена в левой части ребра. Направление вдоль кромки задается увеличением значений параметров. Субдомен 0 - внешний вид геометрии.
e(7,k) - номер поддомена в правой части ребра.
t (треугольники) является 4около-Nt матрица треугольников или 7около-Nt матрица треугольников, в зависимости от того, вызывается ли generateMesh с GeometricOrder пара имя-значение установлена в 'quadratic' или 'linear'соответственно. initmesh создает только 'linear' элементы, имеющие размер 4около-Nt. Nt - количество треугольников в сетке. Каждый столбец t содержит индексы точек в p которые образуют треугольник. Исключением является последняя запись в столбце, которая является номером поддомена. Точки треугольника упорядочены, как показано на рисунке.
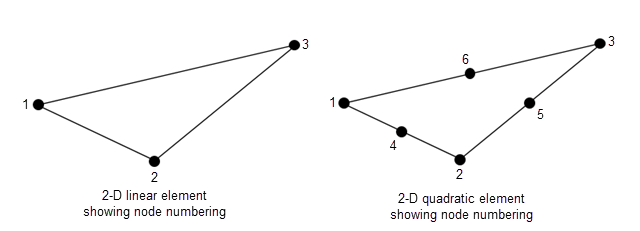
Данные сетки для 3-D сетки имеют следующие компоненты:
p (точки, узлы сетки) 3около-Np матрица узлов, где Np - количество узлов в сетке. Каждый столбец p(:,k) состоит из x-координаты точки k в p(1,k), координата y точки k в p(2,k)и координата z точки k в p(3,k).
e - объект, связывающий грани сети с границами геометрии. Функции панели инструментов дифференциального уравнения в частных производных используют эту связь при преобразовании граничных условий, заданных для геометрических границ, в граничные грани сети.
t (тетраэдры) является либо 11-by-Nt матрица тетраэдров или 5-by-Nt матрица тетраэдров, в зависимости от того, вызывается ли generateMesh с GeometricOrder пара имя-значение установлена в 'quadratic' или 'linear'соответственно. Nt - количество тетраэдров в сетке. Каждый столбец t содержит индексы точек в p которые образуют тетраэдр. Исключение представляет собой последний элемент в столбце, который является номером поддомена. Точки тетраэдра упорядочены, как показано на рисунке.
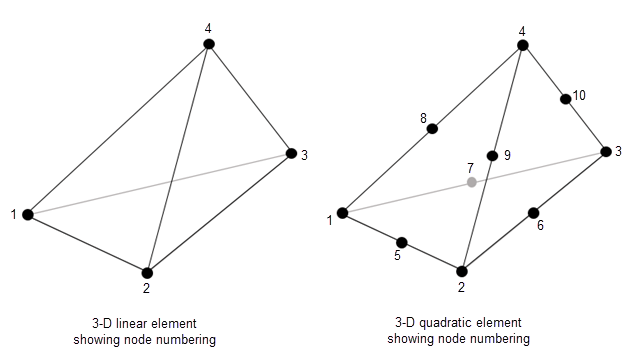
Можно создать [p,e,t] сетка с использованием одного из следующих подходов:
Используйте initmesh для создания 2-D [p,e,t] сетка.
Используйте generateMesh для создания 2-D или 3-D сетки в виде FEMesh объект. Затем используйте meshToPet для преобразования сетки в [p,e,t] сетка.