В этом примере показано, как решить уравнение минимальной поверхности
= 0
на единичном диске Λ = {(x, y) | x2 + y2 ≤ 1}, с u = x2 на граничном ∂Ω.
В этом примере используется приложение PDE Modeler. Программный рабочий процесс см. в разделе Минимальный электрический потенциал.
Эллиптическое уравнение в форме панели инструментов:
au = f
Поэтому для задачи минимальной поверхности коэффициенты следующие:
= 0
Поскольку коэффициент c является функцией решения u, задача минимальной поверхности является нелинейной эллиптической задачей.
Чтобы решить проблему минимальной поверхности в приложении PDE Modeler, выполните следующие действия.
Смоделировать поверхность как единичную окружность.
pdecirc([0 0 1])
Проверьте, что установлен режим приложения Generic Scalar.
Задайте граничные условия. Для этого:
Переключитесь в граничный режим, нажав![]() кнопку или выбрав «Граница» > «Граничный режим».
кнопку или выбрав «Граница» > «Граничный режим».
Выберите все границы, выбрав меню «Правка» > «Выделить все».
Выберите «Граница» > «Задать граничные условия».
Задайте граничное условие Дирихле u = x2. Для этого укажите h = 1, r = x.^2.
Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Определить c = 1./sqrt(1+ux.^2+uy.^2), a = 0, и f = 0.
Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».
Уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».
Выберите нелинейный решатель. Для этого выберите Решение (Solve) > Параметры (Parameters) и установите флажок Использовать нелинейный решатель (Use nonlinear solver). Задайте для параметра допуска значение 0.001.
Решите PDE, выбрав Решение (Solve) > Решение PDE (Solve PDE) или нажав кнопку = на панели инструментов.
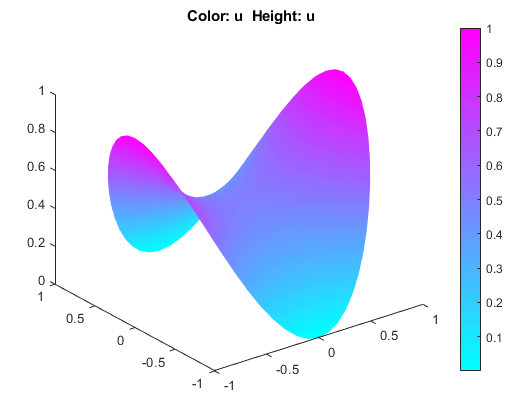
Постройте график решения в 3-D. Для этого выберите PlotParameters. В открывшемся диалоговом окне выберите «Высота» (3-D график).