Exponenta Banner
exponenta event banner

multicuboid

Создание геометрии, образованной несколькими кубическими ячейками

свернуть все на странице

Синтаксис

gm = мультикубоид (W, D, H)
gm = мультикубоид (W, D, H, имя, значение)

Описание

пример

gm = multicuboid(W,D,H) создает геометрию путем объединения нескольких кубических ячеек.

При создании каждого кубоида multicuboid использует следующую систему координат.

пример

gm = multicuboid(W,D,H,Name,Value) создание многокабульной геометрии с использованием одного или нескольких Name,Value аргументы пары.

Примеры

свернуть все

Открыть сценарий в реальном времени

Создайте геометрию, состоящую из трех вложенных кубоидов одинаковой высоты, и включите эту геометрию в модель PDE.

Создайте геометрию с помощью multicuboid функция. Результирующая геометрия состоит из трех ячеек.

gm = multicuboid([2 3 5],[4 6 10],3)
gm = 
  DiscreteGeometry with properties:

       NumCells: 3
       NumFaces: 18
       NumEdges: 36
    NumVertices: 24
       Vertices: [24x3 double]

Создайте модель PDE.

model = createpde
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Включите геометрию в модель.

model.Geometry = gm
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Постройте график геометрии.

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

Figure contains an axes. The axes contains 3 objects of type quiver, patch, line.

Открыть сценарий в реальном времени

Создайте геометрию, состоящую из четырех объединенных кубов, и включите эту геометрию в модель PDE.

Создайте геометрию с помощью multicuboid функции с помощью ZOffset аргумент. Результирующая геометрия состоит из четырех ячеек, расположенных друг над другом.

gm = multicuboid(5,10,[1 2 3 4],'ZOffset',[0 1 3 6])
gm = 
  DiscreteGeometry with properties:

       NumCells: 4
       NumFaces: 21
       NumEdges: 36
    NumVertices: 20
       Vertices: [20x3 double]

Создайте модель PDE.

model = createpde
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Включите геометрию в модель.

model.Geometry = gm
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Постройте график геометрии.

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

Figure contains an axes. The axes contains 3 objects of type quiver, patch, line.

Открыть сценарий в реальном времени

Создайте геометрию, состоящую из одного кубоида, и включите эту геометрию в модель PDE.

Используйте multicuboid для создания одного кубоида. Результирующая геометрия состоит из одной ячейки.

gm = multicuboid(5,10,7)
gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 6
       NumEdges: 12
    NumVertices: 8
       Vertices: [8x3 double]

Создайте модель PDE.

model = createpde
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Включите геометрию в модель.

model.Geometry = gm
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Постройте график геометрии.

pdegplot(model,'CellLabels','on')

Figure contains an axes. The axes contains 3 objects of type quiver, patch, line.

Открыть сценарий в реальном времени

Создайте полый куб и включите его в качестве геометрии в модель PDE.

Создание полого куба с помощью multicuboid функции с помощью Void аргумент. Результирующая геометрия состоит из одной ячейки.

gm = multicuboid([6 10],[6 10],10,'Void',[true,false])
gm = 
  DiscreteGeometry with properties:

       NumCells: 1
       NumFaces: 10
       NumEdges: 24
    NumVertices: 16
       Vertices: [16x3 double]

Создайте модель PDE.

model = createpde
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: []
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Включите геометрию в модель.

model.Geometry = gm
model = 
  PDEModel with properties:

           PDESystemSize: 1
         IsTimeDependent: 0
                Geometry: [1x1 DiscreteGeometry]
    EquationCoefficients: []
      BoundaryConditions: []
       InitialConditions: []
                    Mesh: []
           SolverOptions: [1x1 pde.PDESolverOptions]

Постройте график геометрии.

pdegplot(model,'CellLabels','on','FaceAlpha',0.5)

Figure contains an axes. The axes contains 3 objects of type quiver, patch, line.

Входные аргументы

свернуть все

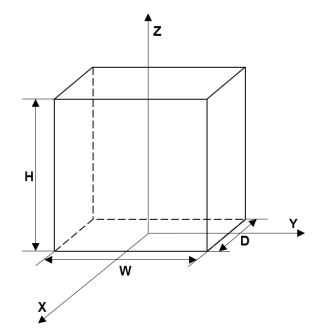
Ширина ячейки, заданная как положительное вещественное число или вектор положительных вещественных чисел. Если W является вектором, то W(i) определяет ширину iТретья ячейка.

Width W, глубина D, и высота H могут быть скалярами или векторами одинаковой длины. Для комбинации скалярных и векторных входных данных: multicuboid реплицирует скалярные аргументы в векторы одинаковой длины.

Примечание

Все ячейки геометрии либо должны иметь одинаковую высоту, либо должны иметь одинаковую ширину и одинаковую глубину.

Пример: gm = multicuboid([1 2 3],[2.5 4 5.5],5)

Глубина ячейки, заданная как положительное вещественное число или вектор положительных вещественных чисел. Если D является вектором, то D(i) определяет глубину iТретья ячейка.

Width W, глубина D, и высота H могут быть скалярами или векторами одинаковой длины. Для комбинации скалярных и векторных входных данных: multicuboid реплицирует скалярные аргументы в векторы одинаковой длины.

Примечание

Все ячейки геометрии либо должны иметь одинаковую высоту, либо должны иметь одинаковую ширину и одинаковую глубину.

Пример: gm = multicuboid([1 2 3],[2.5 4 5.5],5)

Высота ячейки, заданная как положительное вещественное число или вектор положительных вещественных чисел. Если H является вектором, то H(i) определяет высоту iТретья ячейка.

Width W, глубина D, и высота H могут быть скалярами или векторами одинаковой длины. Для комбинации скалярных и векторных входных данных: multicuboid реплицирует скалярные аргументы в векторы одинаковой длины.

Примечание

Все ячейки геометрии либо должны иметь одинаковую высоту, либо должны иметь одинаковую ширину и одинаковую глубину.

Пример: gm = multicuboid(4,5,[1 2 3],'ZOffset',[0 1 3])

Аргументы пары «имя-значение»

Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.

Пример: gm = multicuboid([1 2],[1 2],[3 3],'Void',[true,false])

Смещение по оси Z для каждой ячейки, определяемое как вектор вещественных чисел. ZOffset(i) задает смещение Z iТретья ячейка. Этот вектор должен иметь ту же длину, что и вектор ширины W, вектор глубины D, или вектор высоты H.

Примечание

ZOffset аргумент допустим, только если ширина и глубина постоянны для всех ячеек геометрии.

Пример: gm = multicuboid(20,30,[10 10],'ZOffset',[0 10])

Типы данных: double

Индикатор пустой ячейки, заданный как вектор логического true или false значения. Этот вектор должен иметь ту же длину, что и вектор ширины W, вектор глубины D, или вектор высоты H.

Стоимость true соответствует пустой ячейке. По умолчанию multicuboid предполагает, что все ячейки не пусты.

Пример: gm = multicuboid([1 2],[1 2],[3 3],'Void',[true,false])

Типы данных: double

Выходные аргументы

свернуть все

Объект Geometry, возвращаемый как объект «Свойства геометрии».

Ограничения

  • multicuboid позволяет создавать только геометрии, состоящие из составных или вложенных кубоидов. Для вложенных кубоидов высота должна быть одинаковой для всех ячеек геометрии. Для скомпонованных кубоидов ширина и глубина должны быть одинаковыми для всех ячеек геометрии. Используйте ZOffset аргумент для наложения ячеек друг на друга, не перекрывая их.

  • multicuboid не позволяет создавать вложенные кубоиды одинаковой ширины и глубины. Требование multicuboid(w,d,[h1,h2,...]) не поддерживается.

См. также

| |

Представлен в R2017a

Документация по набору инструментов для дифференциальных уравнений в частных производных

Поддержка