Exponenta Banner
exponenta event banner

Укажите коэффициенты в приложении PDE Modeler

Коэффициенты для скалярных PDE

Для ввода коэффициентов для PDE выберите PDE > PDE Specification.

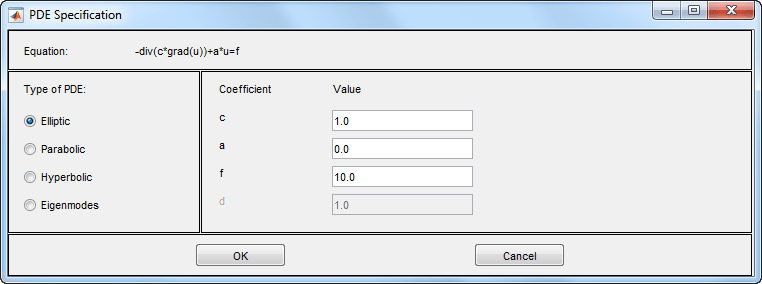
Введите текстовые выражения, используя следующие соглашения:

  • x - координата X

  • y - координата Y

  • u - Решение уравнения

  • ux - Производная u в направлении x

  • uy - Производная u в направлении y

  • t - Время (параболические и гиперболические уравнения)

  • sd - Номер поддомена

Например, это выражение можно использовать для представления коэффициента:

(x + y)./(x.^2 + y.^2 + 1) + 3 + sin(t)./(1 + u.^4)

Для эллиптических проблем при включении u, ux, или uy, необходимо использовать нелинейный решатель. Выберите «Решение» > «Параметры» > «Использовать нелинейный решатель».

Примечание

  • Не используйте кавычки или ненужные пробелы в записях. Синтаксический анализатор может неверно интерпретировать пробел как векторный разделитель, как когда вектор MATLAB ® использует пробел для разделения элементов вектора.

  • Использовать .*, ./, и .^ для операций умножения, деления и возведения в степень. Текстовые выражения работают с векторами строк, поэтому операции должны иметь смысл для векторов строк. Векторы строк - это значения в треугольных центроидах в сетке.

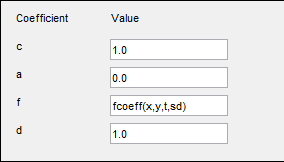
Функции MATLAB можно писать как для коэффициентов, так и для простых текстовых выражений. Например, предположим, что ваш коэффициент f задается файлом fcoeff.m.

function f = fcoeff(x,y,t,sd)

f = (x.*y)./(1 + x.^2 + y.^2); % f on subdomain 1
f = f + log(1 + t); % include time
r = (sd == 2); % subdomain 2
f2 = cos(x + y); % coefficient on subdomain 2 
f(r) = f2(r); % f on subdomain 2

Использовать fcoeff(x,y,t,sd) как коэффициент f в parabolic решатель.

Коэффициент c является матрицей 2 на 2. Можно задать 1-, 2-, 3- или 4-элементные матричные выражения. Разделите выражения для элементов пробелами. Эти выражения означают:

  • 1-элементное выражение: (c00c)

  • 2-элементное выражение: (c (1) 00c (2))

  • 3-элементное выражение: (c (1) c (2) c (2) c (3))

  • 4-элементное выражение: (c (1) c (3) c (2) c (4))

Например, c является симметричной матрицей с постоянными диагональными элементами и cos(xy) в качестве внедиагональных терминов:

1.1 cos(x.*y) 5.5(1)

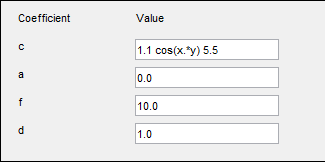
Это соответствует коэффициентам для параболического уравнения

∂u∂t−∇· ((1.1cos (xy) cos (xy) 5,5) ∇u) = 10.

Коэффициенты для систем ПДЭ

Можно ввести коэффициенты для системы с N = 2 уравнения в приложении PDE Modeler. Для этого откройте приложение PDE Modeler и выберите Generic System.

Затем выберите PDE > PDE Specification (Спецификация PDE).

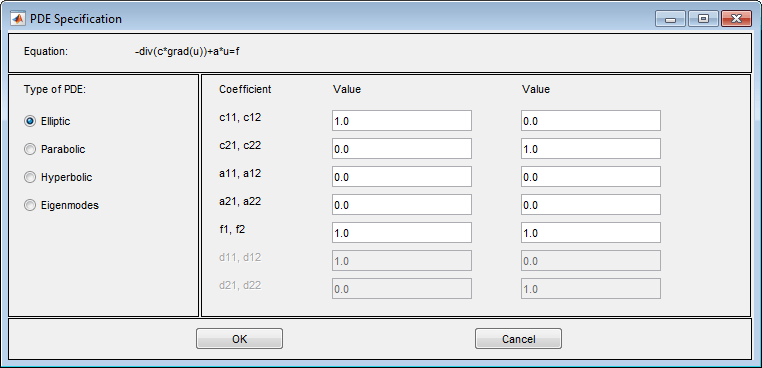
Введите символьные выражения для коэффициентов, используя форму «Коэффициенты для скалярных PDE», с дополнительными опциями для нелинейных уравнений. Дополнительные опции:

  • Представлять i-й компонент раствора u использование 'u(i)' для i = 1 или 2.

  • Аналогично, представляют i-е компоненты градиентов раствора u использование 'ux(i)' и 'uy(i)' для i = 1 или 2.

Примечание

Для эллиптических задач при включении коэффициентов u(i), ux(i), или uy(i), необходимо использовать нелинейный решатель. Выберите «Решение» > «Параметры» > «Использовать нелинейный решатель».

Не используйте кавычки или ненужные пробелы в записях.

Для систем более высокой размерности не используйте приложение PDE Modeler. Представляйте свои коэффициенты проблем в командной строке.

Можно ввести скаляры в c матрица, соответствующая этим уравнениям:

−∇ · (c11∇u1) −∇ · (c12∇u2) +a11u1+a12u2=f1−∇ · (c21∇u1) −∇ · (c22∇u2) +a21u1+a22u2=f2

Если вам нужны матричные версии любой из cij введите выражения, разделенные пробелами. Можно задать 1-, 2-, 3- или 4-элементные матричные выражения. Это означает:

  • 1-элементное выражение: (c00c)

  • 2-элементное выражение: (c (1) 00c (2))

  • 3-элементное выражение: (c (1) c (2) c (2) c (3))

  • 4-элементное выражение: (c (1) c (3) c (2) c (4))

Например, эти выражения показывают один из каждого типа (1-, 2-, 3- и 4-элементные выражения)

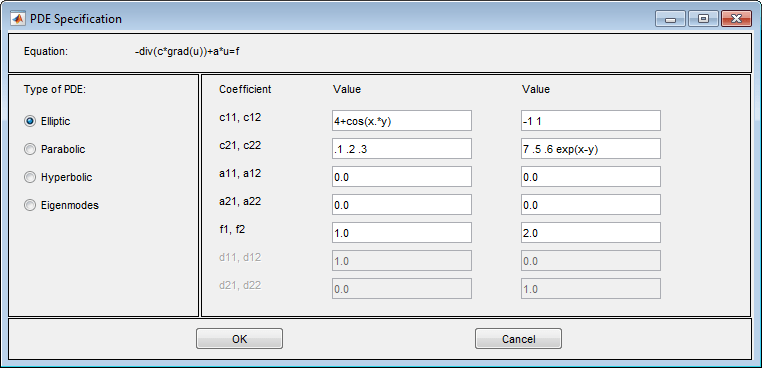
Эти выражения соответствуют уравнениям

−∇· ((4 + cos (xy) 004 + cos (xy)) ∇u1) −∇· ((− 1001) ∇u2) =1−∇· ((.1.2.2.3) ∇u1) −∇· ((7.6.5exp (x − y)) ∇u2) = 2

Коэффициенты, зависящие от времени и пространства

В этом примере показано, как ввести зависящие от времени и координат коэффициенты в приложении PDE Modeler.

Решить параболический PDE,

d∂u∂t−∇⋅ (c∇u) + au = f

со следующими коэффициентами:

  • d = 5

  • a = 0

  • f - линейный наклон до 10, удерживается на 10, затем наклон обратно вниз до 0:

    f = 10 * {10t0≤t≤0.110.1≤t≤0.910−10t0.9≤t≤1

  • c = 1 + .x2 + y2

Чтобы решить это уравнение в приложении PDE Modeler, выполните следующие действия:

  1. Запись файла framp.m и сохраните его на своем пути MATLAB.

    function f = framp(t)

if t <= 0.1
    f = 10*t;
elseif t <= 0.9
    f = 1;
else
    f = 10-10*t;
end
f = 10*f;

  2. Откройте приложение PDE Modeler с помощью pdeModeler команда.

  3. Для отображения линий сетки выберите «Параметры» > «Сетка».

  4. Выровняйте новые фигуры по линиям сетки, выбрав «Параметры» > «Привязка».

  5. Нарисуйте прямоугольник с углами (-1, -0,4), (-1,0,4), (1,0,4) и (1, -0,4). Для этого сначала нажмите кнопку. Затем щелкните один из углов левой кнопкой мыши и перетащите его, чтобы нарисовать прямоугольник.

  6. Нарисуйте окружность с радиусом 0,2 и центром в (0,5,0). Для этого сначала нажмите кнопку. Затем щелкните правой кнопкой мыши начало координат и перетащите курсор, чтобы нарисовать окружность. Щелчок правой кнопкой мыши ограничивает нарисованную форму так, что она является окружностью, а не эллипсом. Если окружность не является идеальной единицей измерения, дважды щелкните ее. В открывшемся диалоговом окне укажите точное местоположение центра и радиус окружности.

  7. Моделирование геометрии путем ввода R1-C1 в поле Задать формулу.

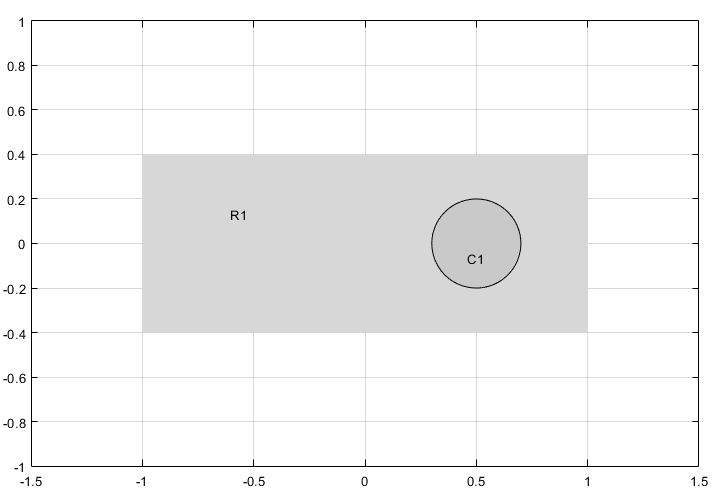
  8. Убедитесь, что установлен режим приложения Generic Scalar.

  9. Задайте граничные условия. Для этого переключитесь в граничный режим, выбрав «Граница» > «Граничный режим». Используйте клавиши SHIFT + щелчок для выбора нескольких границ. Затем выберите «Граница» > «Задать граничные условия».

    • Для прямоугольника используйте граничное условие Дирихле с h = 1 и r = t*(x-y).

    • Для окружности используйте граничное условие Неймана с g = x.^2+y.^2 и q = 1.

  10. Задайте коэффициенты, выбрав PDE > PDE Specification или нажав кнопку PDE на панели инструментов. Выберите параболический тип PDE. Определить c = 1+x.^2+y.^2, a = 0, f = framp(t), и d = 5.

    Примечание

    Не включайте кавычки или пробелы при указании коэффициентов в приложении PDE Modeler. Синтаксический анализатор интерпретирует все входные данные как векторы символов. Он может неверно интерпретировать пространство как векторный разделитель, как когда вектор MATLAB использует пространство для разделения элементов вектора.

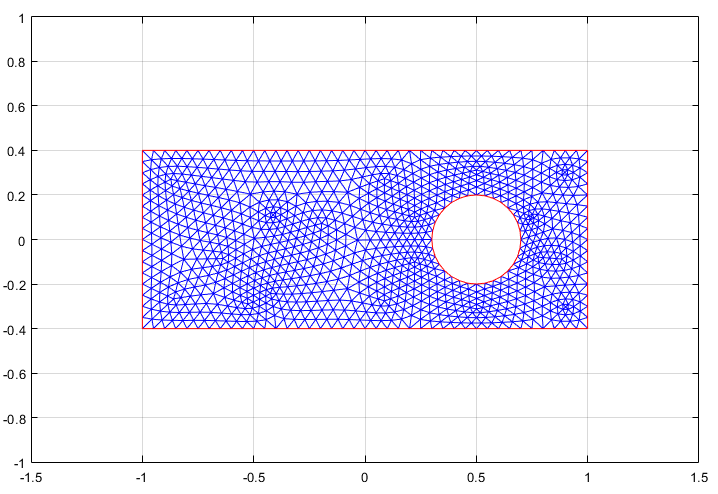
  11. Инициализируйте сетку, выбрав меню «Сетка» > «Инициализировать сетку».

  12. Дважды уточните сетку, выбрав меню «Сетка» > «Уточнить сетку».

  13. Улучшите качество треугольника, выбрав меню «Сеть» > «Сгиб сетки».

  14. Задайте начальное значение и время решения. Для этого выберите «Решение» > «Параметры».

    В открывшемся диалоговом окне задайте время равным linspace(0,1,50) и начальное значение u (t0) для0.

  15. Решите уравнение, выбрав команду Решить (Solve) > Решить PDE (Solve PDE) или нажав кнопку = на панели инструментов.

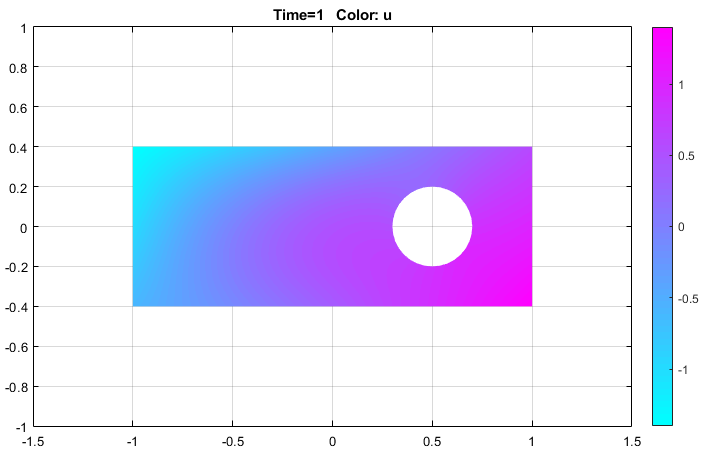
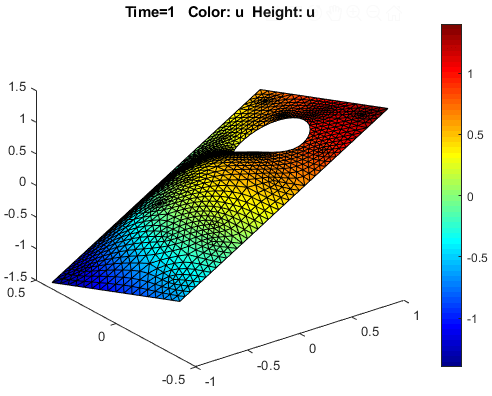
  16. Визуализация решения как 3-D статического графика. Для этого:

    1. Выберите «Печать» > «Параметры».

    2. В открывшемся диалоговом окне выберите параметры «Цвет и высота» (3-D печать).

    3. Выберите опцию Показать сетку (Show mesh).

    4. Измените карту цветов на jet с помощью соответствующего раскрывающегося меню в том же диалоговом окне.

Документация по набору инструментов для дифференциальных уравнений в частных производных

Поддержка