Документация

Создание 2-D геометрии в приложении PDE Modeler

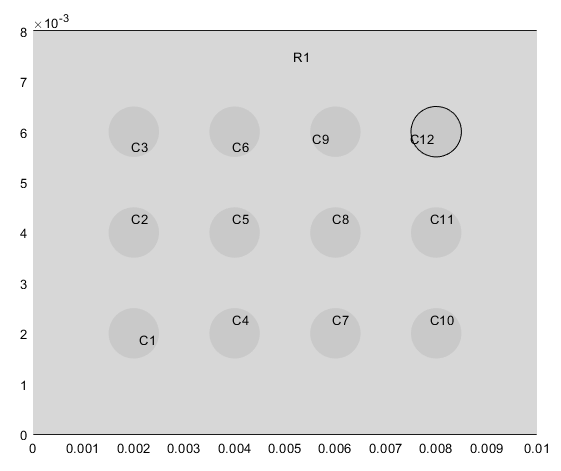
Создайте геометрию в приложении PDE Modeler. Сначала откройте приложение PDE Modeler с геометрией, состоящей из прямоугольника и 12 окружностей.

pderect([0 0.01 0 0.008])
for i = 0.002:0.002:0.008
   for j = 0.002:0.002:0.006
       pdecirc(i,j,0.0005)
   end
end

Скорректируйте границы осей, выбрав Опции (Options) > Границы осей (Axes Limits). Выберите «Авто», чтобы использовать автоматическое масштабирование для обеих осей.

Экспортируйте матрицу описания геометрии, формулу набора и матрицу пространства имен в рабочее пространство MATLAB ®, выбрав команду «Рисование» > «Экспорт описания геометрии», «Задать формулу», «Метки». Эти данные позволяют реконструировать геометрию в рабочем пространстве.

Вытесните 2-ю геометрию в 3D геометрию теплоотвода

В окне команд MATLAB используйте decsg функция для разложения экспортированной геометрии на минимальные области. Постройте график результата.

g = decsg(gd,sf,ns);
pdegplot(g,'FaceLabels','on')

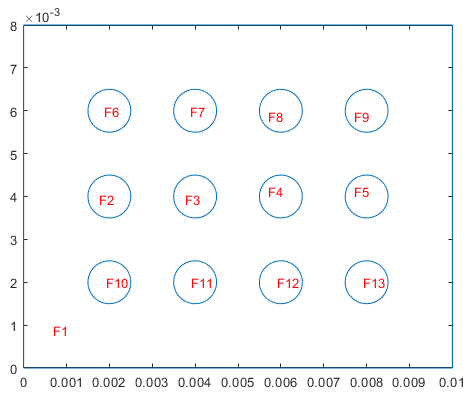
Создайте тепловую модель для нестационарного анализа.

model = createpde('thermal','transient');

Создайте 2-D геометрию из матрицы разложенной геометрии и назначьте геометрию тепловой модели.

g = geometryFromEdges(model,g);

Вытяните геометрию 2-D вдоль оси Z на 0,0005 единиц.

g = extrude(g,0.0005);

Постройте график выдавленной геометрии, чтобы можно было видеть метки граней сверху.

figure
pdegplot(g,'FaceLabels','on')
view([0 90])

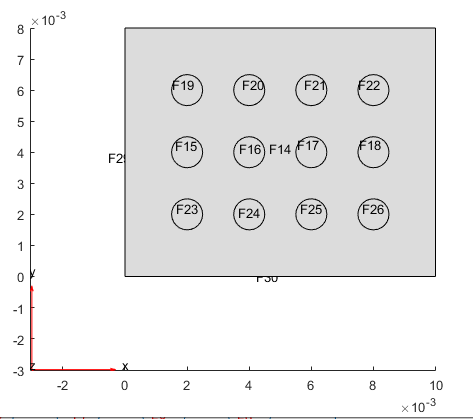
Вытяните круговые грани (грани с идентификаторами от 15 до 26) вдоль оси Z еще на 0,005 единиц. Эти поверхности образуют ребра теплоотвода.

g = extrude(g,[15:26],0.005);

Назначьте измененную геометрию тепловой модели и постройте ее график.

model.Geometry = g;
figure
pdegplot(g)

Выполнение теплового анализа

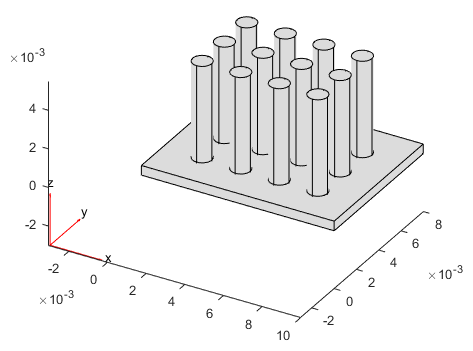
Предположим, что теплоотвод изготовлен из меди, укажите теплопроводность, массовую плотность и удельную теплоту.

thermalProperties(model,'ThermalConductivity',400, ...
                        'MassDensity',8960, ...
                        'SpecificHeat',386);

Задайте постоянную Штефана-Больцмана.

model.StefanBoltzmannConstant = 5.670367e-8;

Наложите граничное условие температуры на нижнюю поверхность теплоотвода, состоящего из 13 граней.

thermalBC(model,'Face',1:13,'Temperature',1000);

Укажите параметры конвекции и излучения на всех остальных поверхностях теплоотвода.

thermalBC(model,'Face',14:g.NumFaces, ...
                'ConvectionCoefficient',5, ...
                'AmbientTemperature',300, ...
                'Emissivity',0.8);

Установите начальную температуру всех поверхностей на температуру окружающей среды.

thermalIC(model,300);

Создайте сетку.

generateMesh(model);

Решите нестационарную тепловую проблему для времени от 0 до 0,0075 секунд с шагом времени 0,0025 секунд.

results = solve(model,0:0.0025:0.0075);

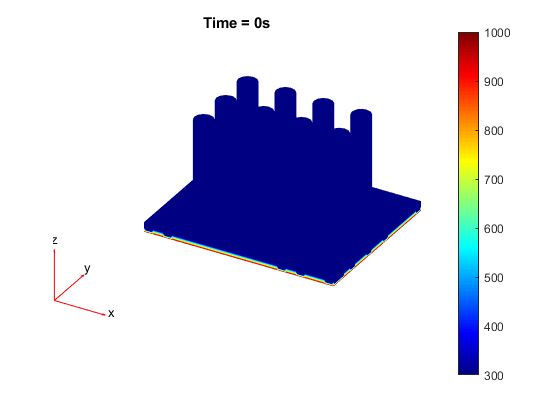
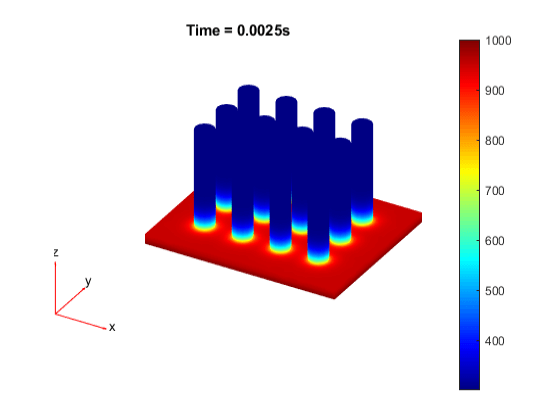
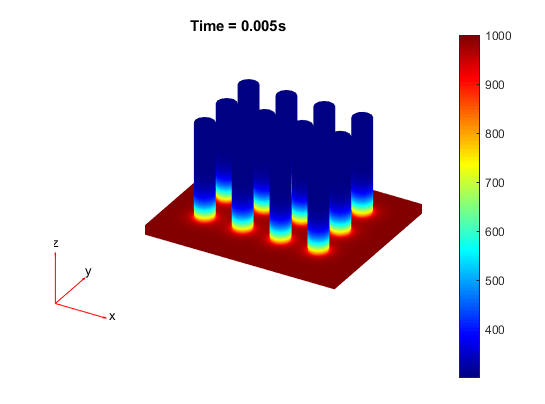
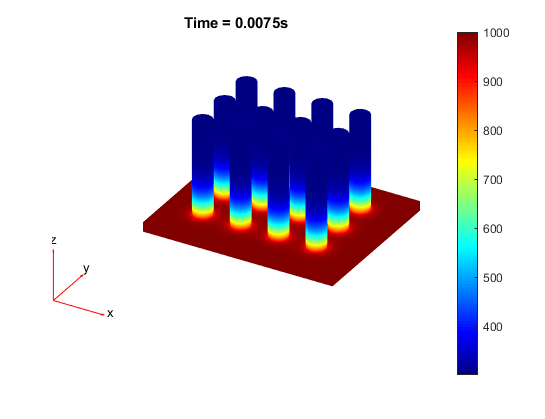
Постройте график распределения температуры для каждого временного шага.

for i = 1:length(results.SolutionTimes)
  figure
  pdeplot3D(model,'ColorMapData',results.Temperature(:,i))
  title({['Time = ' num2str(results.SolutionTimes(i)) 's']})
end