Документация

Концепция радиолокационного куба данных

Куб радиолокационных данных является удобным способом концептуального представления пространственно-временной обработки. Чтобы построить куб радиолокационных данных, предположим, что предварительная обработка преобразует радиочастотные сигналы, принятые от множества импульсов по множеству элементов матрицы, в комплексные выборки основной полосы частот. Упорядочить комплексные выборки основной полосы в трехмерный массив размером K-by-N-by-L.

Многие операции по обработке радиолокационных сигналов в программном обеспечении Phased Array System Toolbox™ соответствуют обработке низкоммерных подмножеств куба радиолокационных данных. Подмножество может быть одномерным субвектором или двумерной субматрицей.

На следующем рисунке показана организация куба радиолокационных данных в данном программном обеспечении. В последующих разделах объясняется каждый из измерений и то, какой аспект пространственно-временной обработки они представляют.

Быстрые выборки времени

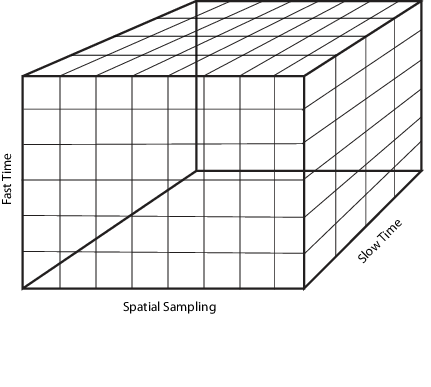
Рассмотрим K-by-1 субвектор куба радиолокационных данных вдоль оси быстрого времени на предыдущей диаграмме. Каждый вектор столбца представляет набор комплексных отсчетов основной полосы из одного импульса в одном элементе массива, дискретизированного в $${}_{\mathrm{rateF}}$$. Эта частота дискретизации является самой высокой частотой дискретизации системы и приводит к быстрому времени назначения. Выберите частоту выборки, $${\mathrm{Fs}}_{,}$$достаточно большую, чтобы избежать наложения. Соответствующий интервал выборки равен Ts $${}_{=}\mathrm{}{}_{\mathrm{1/Fs}}$$. Измерение быстрого времени также называется измерением диапазона. Быстрые интервалы выборки времени при преобразовании в расстояние с использованием скорости распространения сигнала часто называют ячейками диапазона или элементами диапазона.

Импульсное сжатие является примером операции обработки сигнала, выполняемой для быстрых отсчетов времени. Другим примером обработки сигнала является дехирпирование. В этих типах операций количество выборок в первом измерении выходного сигнала может отличаться от входного.

Образцы замедленного времени

Рассмотрим каждую подматрицу K-by-L куба данных РЛС. Подматрица содержит K векторов строк с размерными 1-by-L. Каждый из этих векторов строк содержит комплексные выборки основной полосы частот из L различных импульсов из одного и того же бина диапазона. Существует матрица K-by-L для каждого из N элементов массива. Интервал дискретизации между L выборками является интервалом повторения импульсов (PRI). Типичные PRIs намного длиннее интервала быстрой выборки. Из-за длинных интервалов дискретизации выборки, взятые через множество импульсов, называются медленным временем.

Обработка данных в медленном измерении позволяет оценить доплеровский спектр в заданном бункере диапазона. В этом типе операций количество выборок в третьем измерении куба данных может изменяться. Количество доплеровских ячеек не обязательно равно количеству импульсов.

Критерий Найквиста в равной степени применим к медленному измерению. Ответной частотой PRI является частота повторения импульсов (PRF). PRF дает ширину однозначного доплеровского спектра.

Пространственная выборка

Фазированные массивы состоят из нескольких элементов массива. Рассмотрим каждую подматрицу K-by-N куба данных РЛС. Каждый вектор столбца состоит из K быстрых отсчетов для одного импульса, принятого в одном элементе матрицы. N векторов столбцов представляют один и тот же импульс, дискретизированный по N элементам матрицы. Дискретизированные данные в N векторах столбцов представляют собой пространственную выборку формы падающего сигнала. Анализ данных по элементам массива позволяет определить пространственное частотное содержание каждого принятого импульса. Критерий Найквиста для пространственной выборки требует, чтобы элементы матрицы не были разделены более чем на половину длины волны несущей частоты.

В операциях с пространственной частотой количество выборок во втором измерении куба данных может изменяться. Количество пространственных частотных ячеек не обязательно равно количеству сенсорных элементов.

Формирование луча - это операция пространственной фильтрации, которая объединяет данные по элементам массива для избирательного усиления и подавления волновых полей, падающих на массив с конкретных направлений.

Пространственно-временная обработка

Пространственно-временная адаптивная обработка работает на двумерных данных угла-доплера для каждого элемента диапазона. Рассмотрим куб данных РЛС K-by-N-by-L. Каждая из К выборок представляет собой данные из одного и того же диапазона. Этот диапазон дискретизируется по N элементам массива и L PRIs. Свертывание трехмерной матрицы на каждом бункере диапазона в подматрицы N-by-L позволяет осуществлять одновременный двумерный анализ угла прихода и доплеровской частоты.

Организация данных в кубе радиолокационных данных

При наличии К комплексных отсчетов данных основной полосы, собранных из L импульсов, полученных N датчиками, можно организовать данные в формате, совместимом с правилами набора инструментов системы фазированных массивов, используя permute. После обработки данных можно преобразовать обратно в исходный формат куба данных с помощью ipermute.

origdata = randn(6,10,200)+1j*randn(6,10,200);

newdata = permute(origdata,[3 1 2]);

data = ipermute(newdata,[3 1 2]);