Поляризованные поля

Введение в поляризацию

Программное обеспечение Phased Array System Toolbox™ можно использовать для моделирования радиолокационных систем, которые передают, распространяют, отражают и принимают поляризованные электромагнитные поля. С помощью этой возможности инструментарий может реалистично моделировать взаимодействие радиолокационных волн с целями и окружающей средой.

Основным свойством плоских волн в свободном пространстве является то, что направления векторов электрического и магнитного полей ортогональны направлению их распространения. Направление распространения электромагнитной волны определяется вектором Пойнтинга

$S = E$ × H

В этом уравнении Е представляет электрическое поле, а Н представляет магнитное поле. Величина S представляет величину и направление потока энергии волны. Уравнения Максвелла, применяемые к плоским волнам, дают результат, что электрическое и магнитное поля связаны

$\begin{array}{l} E & = - \\ Zs & \frac{×}{} HH \end{array}$ = 1Zs × E

Вектор s, единичный вектор в направлении S, представляет направление распространения волны. Величина Z является волновым сопротивлением и является функцией электрической диэлектрической проницаемости и магнитной проницаемости среды, в которой проходит волна.

После манипулирования двумя уравнениями можно увидеть, что электрическое и магнитное поля ортогональны направлению распространения

$E \cdot s = H ·$ s = 0.

Этот последний результат доказывает, что действительно существуют только две независимые компоненты электрического поля, обозначенные _Ex и _Ey. Аналогично, магнитное поле может быть выражено в виде двух независимых компонентов. Из-за ортогональности полей электрическое поле может быть представлено в виде двух единичных векторов, ортогональных направлению распространения.

$E =_{} {\overset{}{}}_{Exe}^_{} {\overset{}{x}}_{+}$ глаз ^ y

Единичные векторы вместе с единичным вектором в направлении распространения

${{\overset{}{e}}_{^} {\overset{,}{x}}_{} e^$ y, s}.

образуют правостороннюю ортонормированную триаду. Позднее эти векторы и определенные ими координаты будут связаны с координатами конкретной радиолокационной системы. В радиолокационных системах принято использовать индексы H и V, обозначающие горизонтальную и вертикальную составляющие, вместо x и y. Поскольку электрическое и магнитное поля определяются друг другом, необходимо учитывать только свойства электрического поля.

Для радиолокационной системы электрическое и магнитное поле на самом деле являются сферическими волнами, а не плоскими волнами. Однако на практике эти поля обычно измеряются в дальней области поля или зоне излучения радиолокационного источника и представляют собой приблизительно плоские волны. В дальнем поле волны называются квазиплоскостными волнами. Точка лежит в дальнем поле, если ее расстояние R от источника удовлетворяет R ^≫D2/λ где D - типичный размер источника, будь то одиночная антенна или решетка антенн.

Поляризация применяется к чисто синусоидальным сигналам. Наиболее общее выражение для синусоидальной плоскости-волны имеет вид

$_{} E=Ex0cos (ωt-k \cdot x_{} +ϕx {\overset{}{)}}_{}_{} e^x+Ey0cos (ωt-k \cdot_{x} {\overset{+ϕy}{}}_{)}_{} {\overset{}{}}_{}_{} {\overset{}{}}_{}$ e^y=Exe^x+Eye^y

Величины _Ex0 и _Ey0 представляют собой действительные, неотрицательные амплитуды компонентов электрического поля, а _{δ x} и _{λ y} являются фазами поля. Это выражение является наиболее общим для поляризованной волны. Электромагнитная волна поляризуется, если отношение амплитуд ее составляющих и разности фаз между ней не изменяется со временем. Определение поляризации может быть расширено для включения узкополосных сигналов, для которых ширина полосы мала по сравнению с центральной или несущей частотой сигнала. Отношение амплитуд и разность фаз медленно изменяются со временем по сравнению с периодом волны и могут рассматриваться как постоянные во многих колебаниях.

Обычно можно подавить пространственную зависимость поля и записать вектор электрического поля как

$_{} E=Ex0cos (ωt_{} +ϕx {\overset{}{)}}_{}_{} e^x+Ey0cos (_{ωt} {\overset{+ϕy}{}}_{)}_{} {\overset{}{}}_{}_{} {\overset{}{}}_{}$ e^y=Exe^x+Eye^y

Линейная и круговая поляризация

Предыдущее уравнение для поляризованной плоской волны показывает, что кончик двумерного вектора электрического поля движется вдоль траектории, которая лежит в плоскости, ортогональной направлению распространения поля. Форма траектории зависит от величин и фаз компонентов. Например, если _ϕx = _ϕy, Вы можете удалить временную зависимость и написать

$_{Ey} \frac{=_{}}{_{}}_{}$ Ey0Ex0Ex

Это уравнение представляет прямую линию через начало координат с положительным наклоном. И наоборот, предположим, Затем кончик вектора электрического поля следует по прямой через начало координат с отрицательным наклоном

$_{Ey} = \frac{_{-}}{_{}}_{}$ Ey0Ex0Ex

Эти два случая поляризации названы линейными поляризованными, потому что поле всегда колеблется вдоль прямой в ортогональной плоскости. Если _Ex0 = 0, поле является вертикально поляризованным, а если _Ey0 = 0 - горизонтально поляризованным.

Другой случай возникает, когда амплитуды одинаковы, _Ex = _Ey, но фазы отличаются на ± δ/2

$\begin{array}{l} _{} & _{} Ex=E0cos (ωt +ϕ \\ )_{} & _{} Ey=E0cos (ωt +ϕ\pmπ/2)_{} = \mpE0sin ( \end{array}$ ωt +ϕ)

Возведя обе стороны в квадрат, можно показать, что кончик вектора электрического поля подчиняется уравнению окружности

$_{}^{}_{}^{}_{}^{Ex2+Ey2=E02}$

Хотя это уравнение дает путь, по которому проходит вектор, оно не указывает, в каком направлении вектор электрического поля движется по окружности. Он вращается по часовой стрелке или против часовой стрелки? Направление вращения зависит от знака δ/2 в фазе. Эту зависимость можно увидеть, проверив движение вершины векторного поля. Примите общий угол фазы, ϕ = 0. Это предположение допустимо, поскольку общая фаза определяет только начальное положение вектора и не изменяет форму его траектории. Во-первых, посмотрите на случай + δ/2 для волны, проходящей вдоль s-направления (вне страницы). При t = 0 вектор указывает вдоль оси X. Через четверть периода вектор указывает на отрицательную ось y. Через еще четверть периода он указывает вдоль отрицательной оси X.

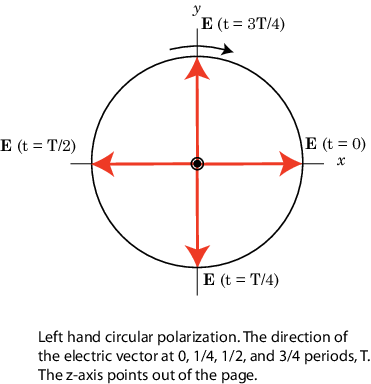
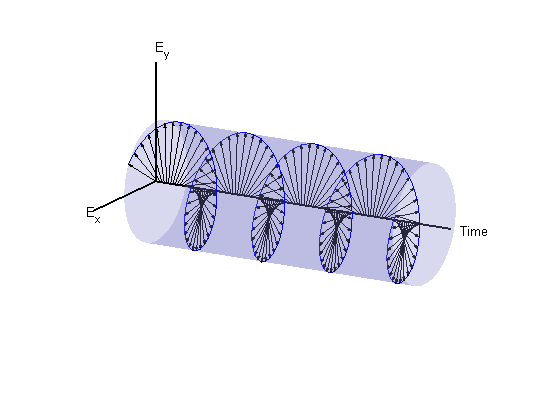
MATLAB ® использует соглашение IEEE для присвоения имен правой или левой поляризации направлению вращения электрического вектора, а не по часовой стрелке или против часовой стрелки. При использовании этого соглашения левую или правую руку определяют, указывая левым или правым большим пальцем вдоль направления распространения волны. Затем выровняйте кривую пальцев по направлению вращения поля в заданной точке пространства. Если поворот следует кривой левой руки, то волна поляризуется левой. Если поворот следует кривой правой руки, то волна поляризуется правой рукой. В предыдущем сценарии поле имеет левую круговую поляризацию (LHCP). Разность фаз -δ/2 соответствует правой круговой поляризованной волне (RHCP). На следующем рисунке представлен трехмерный вид электромагнитной волны LHCP при ее движении в s-направлении.

Когда используются термины по часовой стрелке или против часовой стрелки, они зависят от того, как вы смотрите на волну. Если смотреть вдоль направления распространения, то направление по часовой стрелке соответствует правой поляризации и против часовой стрелки соответствует левой поляризации. Если смотреть в сторону, откуда идет волна, то по часовой стрелке соответствует левая поляризация и против часовой стрелки соответствует правая поляризация.

Левая круговая поляризация

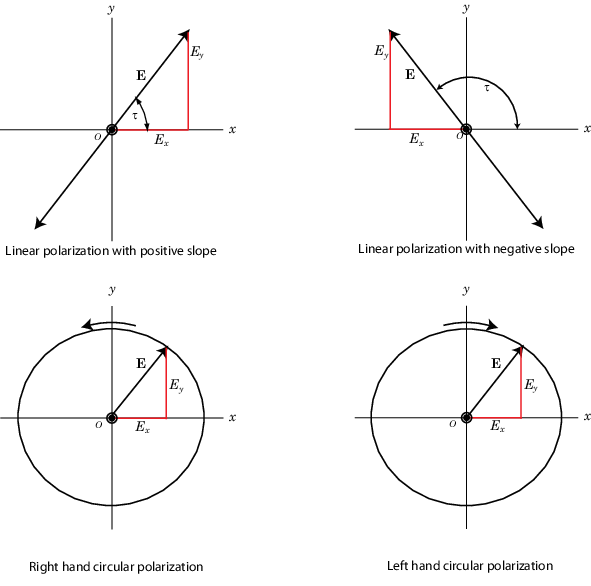
На рисунке ниже показано появление линейных и круговых поляризованных полей при их движении к вам вдоль s-направления.

Линейная и круговая поляризация

Эллиптическая поляризация

Кроме линейного и кругового состояний поляризации, третий тип поляризации - эллиптическая поляризация. Эллиптическая поляризация включает в себя линейную и круговую поляризацию как особые случаи.

Как и при линейной или круговой поляризации, можно удалить временную зависимость для получения локуса точек, которые перемещает кончик вектора электрического поля

${(\frac{_{}}{_{ExEx0}})}^{} 2 {\frac{+_{}}{(_{}}}^{} EyEy0) \frac{2_{}}{-_{2}} (\frac{_{}}{_{ExEx0}}) ({EyEy0)}^{}$ cos

В этом случае λ = _фу - _фх. Это уравнение представляет наклонный двумерный эллипс. Его размер и форма определяются амплитудами составляющих и разностью фаз. Наличие поперечного члена указывает на то, что эллипс наклонен. Уравнение не дает никакой информации о направлении вращения, как в случае круговой поляризации. Например, на следующем рисунке показано мгновенное состояние электрического поля, но не показано направление, в котором вращается поле.

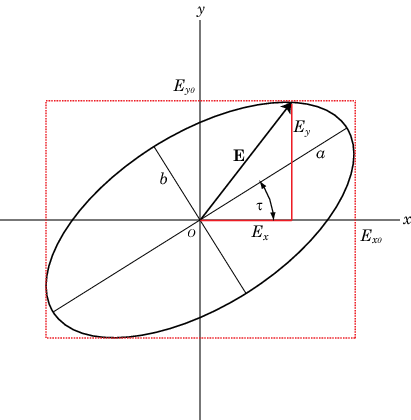
Размер и форма двумерного эллипса могут определяться тремя параметрами. Эти параметры являются длинами двух его осей, большой полуоси, a и малой полуоси, b, и угла наклона На следующем рисунке показаны три параметра наклонного эллипса. Их можно получить из двух амплитуд электрического поля и разности фаз.

Поляризационный эллипс

Поляризацию лучше всего понимать с точки зрения комплексных сигналов. Комплексное представление поляризованной волны имеет вид

$E =_{}^{_{}}^{} {\overset{}{}}_{Ex0eiϕxeiωte}^_{x}^{+_{}}^{} {\overset{}{}}_{}_{Ey0eiϕyeiωte}^^{y_{}} {\overset{}{=}}_{(}_{}^{_{Ex0eiϕxe}} {\hat{}}_{} x^{+}$ Ey0eiϕye ^ y) eiü t

Определить коэффициент комплексной поляризации как отношение комплексных амплитуд

$start= \frac{_{}}{_{}}^{{Ey0Ex0ei}_{} (_{starty}} - \frac{_{startx}}{)_{=}}^{}$ Ey0Ex0ei

где start= _starty - _{λ x}.

Полезно ввести вектор поляризации. Для вышеуказанного комплексного поляризованного электрического поля вектор поляризации P получают нормализацией электрического поля.

$P \frac{=_{}}{_{}} {\overset{}{}}_{Ex0Eme} \frac{^_{x}}{_{+}}^{_{}_{Ey0Emei (}} {\overset{}{}}_{} \frac{_{}}{_{}} {\overset{}{}}_{} \frac{_{}}{_{}}^{} {\overset{}{}}_{}$

где _Em2 = _Ex02 + _Ey02 - величина волны.

Общий размер поляризационного эллипса не важен, потому что он может изменяться по мере прохождения волны через пространство, особенно через геометрическое затухание. Важно иметь форму эллипса. Таким образом, значимыми параметрами эллипса являются отношение размеров его оси, a/b, называемое осевым отношением, и угол наклона, Обе эти величины могут быть определены по отношению амплитуд составляющих и разности фаз или, что эквивалентно, по отношению поляризации. Другой величиной, эквивалентной осевому соотношению, является угол эллиптичности, λ.

В программном обеспечении Phased Array System Toolbox можно использовать polratio функция преобразования комплексных амплитуд fv=[Ey;Ex] к коэффициенту поляризации.

p = polratio(fv)

Угол наклона

Угол наклона определяется как положительный (против часовой стрелки) угол поворота от оси X к большой полуоси эллипса. Из-за свойств симметрии эллипса угол наклона, τ, должен только быть определенным в диапазоне-π/2 ≤ τ ≤ π/2. Угол наклона можно найти, определив повернутую систему координат, в которой полукоординатные и полукоординатные оси выравниваются с повернутыми координатными осями. Тогда уравнение эллипса не имеет перекрестных членов. Решение принимает форму

$tan2τ = \frac{_{}_{}}{_{}^{}_{}^{}} 2Ex0Ey0Ex02−Ey02cosϕ$

где ü = _фy - _фх. Обратите внимание, что это уравнение можно переписать строго в терминах отношения амплитуд и разности фаз.

Осевое отношение и угол эллиптичности

После решения угла наклона можно определить длину основной и малой полуосей. Концептуально эллипс поворачивается по часовой стрелке на угол наклона и измеряет длины пересечений эллипса с осями x и y. Точкой пересечения с большим значением является большая полуось, a, а точкой пересечения с меньшим значением является малая полуось, b.

Осевое отношение определяется как AR = a/b и по конструкции всегда больше или равно единице. Угол эллиптичности определяется

$\frac{}{tanε=∓ba}$

и всегда лежит в диапазоне-λ/4 ≤ start ≤ λ/4.

Если определить вспомогательный угол, α, по

$tanα \frac{=_{}}{_{}}$ Ey0Ex0

затем угол эллиптичности задается как

$sin2ε = sin2αsinϕ$

И осевое отношение, и угол эллиптичности определяются из отношения амплитуд и разности фаз и не зависят от общей величины поля.

Чувство вращения

Для эллиптической поляризации, как и для круговой поляризации, необходим ещё один параметр для полного описания эллипса. Этот параметр должен обеспечивать значение вращения или направление, в котором кончик электрического (или магнитного вектора) перемещается во времени. Скорость изменения угла, который вектор поля делает с x-осью, пропорциональна -sin, где start- разность фаз. При положительном значении sin, скорость изменения отрицательна, что указывает на то, что поле имеет левую поляризацию. При отрицательной скорости изменения - положительная или правосторонняя поляризация.

Функция polellip позволяет найти значения параметров эллипса поляризации из вектора компонента поля fv=[Ey;Ex] или коэффициент поляризации, p.

fv=[Ey;Ex];
[tau,epsilon,ar,rs] = polellip(fv);
p = polratio(fv);
[tau,epsilon,ar,rs] = polellip(p);

Переменные tau, epsilon, ar и rs представляют угол наклона, угол эллиптичности, осевое отношение и значение угла поворота соответственно. Оба синтаксиса дают одинаковый результат.

Сводка значений поляризации

Эта таблица суммирует несколько различных общих состояний поляризации и значения амплитуд, фаз и коэффициента поляризации, которые их производят:

Поляризация	Амплитуды	Фазы	Коэффициент поляризации
Линейный положительный уклон	Любые неотрицательные вещественные значения для _Ex, _Ey.	_фу = _фх	Любое неотрицательное вещественное число
Линейный отрицательный уклон	Любые неотрицательные вещественные значения для _Ex, _Ey	_фу = _фх + δ	Любое отрицательное вещественное число
Праворульный циркуляр	_Ex = Ey	_фy = _фх- δ/2	-i
Левосторонний круговой	_Ex = Ey	_фу = _фх + δ/2	я
Праворукая эллиптическая	Любые неотрицательные вещественные значения для _Ex, _Ey	sin (_фy- _фх) < 0	sin (arg start) < 0
Левая эллиптическая	Любые неотрицательные вещественные значения для _Ex, _Ey	sin (_фy- _фх) > 0	sin (arg start) > 0

Основания линейной и круговой поляризации

Как показано ранее, можно выразить поляризованное электрическое поле как линейную комбинацию базисных векторов вдоль направлений x и y. Например, комплексные векторы электрического поля для волны с правой круговой поляризацией (RHCP) и волны с левой круговой поляризацией (LHCP) принимают вид:

$E = {Re}_{} [_{E0} (_{}^{ex\mpiey) ei}$ (

В этом уравнении положительный знак для поля LHCP, а отрицательный знак для поля RHCP. Этим двум особым комбинациям можно присвоить новое имя. Определение нового набора базисных векторов, называемого циклическим набором базисных векторов

$\begin{array}{l} _{er} \frac{=}{\sqrt{}} 12_{} ({ex}_{} - \\ _{} \frac{iey}{\sqrt{)}}_{el} =_{} 12 \end{array}$ (ex + iey)

Можно выразить любое поляризованное поле в виде циклического базисного набора вместо линейного базисного набора. И наоборот, можно также записать базис линейной поляризации в терминах базиса круговой поляризации

$\begin{array}{l} _{ex} & \frac{=}{\sqrt{}} 12_{} (_{er} \\ +_{} & \frac{el}{\sqrt{)}} {ey}_{} =_{} \end{array}$ 12i (er − el)

Любое общее эллиптическое поле может быть записано как комбинация круговых базисных векторов

$E =_{}_{} {Элель}_{} +_{}$ Эрер

Вектор Джонса

Поляризованное поле ортогонально направлению распространения волны. Таким образом, поле может быть полностью задано двумя комплексными компонентами вектора электрического поля в плоскости поляризации. Состав поляризованной волны в терминах двухкомпонентных векторов называется составом вектора Джонса. Состав вектора Джонса может быть выражен либо в линейном базисе, либо в круговом базисе, либо в любом базисе. В этой таблице показано представление общих поляризаций в линейном базисе и круговом базисе.

Общие поляризации	Вектор Джонса в линейном базисе	Вектор Джонса в круговой основе
Вертикальный	`[0;1]`	`1/sqrt(2)*[-1;1]`
Горизонтальный	`[1;0]`	`1/sqrt(2)*[1;1]`
45 ° Линейный	`1/sqrt(2)*[1;1]`	`1/sqrt(2)*[1-1i;1+1i]`
135 ° Линейный	`1/sqrt(2)*[1;-1]`	`1/sqrt(2)*[1+1i;1-1i]`
Правый круговой	`1/sqrt(2)*[1;-1i]`	`[0;1]`
Левый круговой	`1/sqrt(2)*[1;1i]`	`[1;0]`

Параметры Стокса и сфера Пуанкаре

Поляризационный эллипс является мгновенным представлением поляризованной волны. Однако его параметры, угол наклона и угол эллиптичности, часто не поддаются непосредственному измерению, особенно на очень высоких частотах, таких как световые частоты. Однако можно определить поляризацию по измеряемым интенсивностям поляризованного поля.

Измеряемыми интенсивностями являются параметры Стокса, _S0, _S1, _S2 и _S3. Первый параметр Стокса, _S0, описывает общую интенсивность поля. Второй параметр, _S1, описывает преобладание линейной горизонтально поляризованной интенсивности над линейной вертикально поляризованной интенсивностью. Третий параметр, _S2, описывает преобладание линейно + 45 ° поляризованной интенсивности над линейно 135 ° поляризованной интенсивностью. Наконец_, S3 описывает преобладание интенсивности правой круговой поляризации над интенсивностью левой круговой поляризации. Параметры Стокса определяются как

$\begin{array}{l} _{} & _{}^{}_{}^{} \\ _{} & _{}^{}_{}^{} \\ _{} & _{}_{} \\ _{} & _{}_{} S0=Ex02+Ey02S1=Ex02−Ey02S2=2Ex0Ey0cosϕS3=2Ex0Ey0sinϕ \end{array}$

Для полностью поляризованных полей можно показать усреднение по времени уравнения эллипса поляризации, что

$_{}^{}_{}^{}_{}^{}_{}^{S02=S12+S22+S32}$

Таким образом, существует только три независимых параметра Стокса.

Для частично поляризованных полей, напротив, параметры Стокса удовлетворяют неравенству

$_{}^{S02} <_{}^{}_{}^{}_{}^{S12+S32+S32}$

Параметры Стокса соотносятся с углами наклона и эллиптичности

$\begin{array}{l} _{} & _{} \\ _{} & _{} \\ _{} & _{} S1=S0cos2τcos2εS2=S0sin2τcos2εS3=S0sin2ε \end{array}$

и обратно по

$\begin{array}{l} tan2τ & = \frac{_{}}{_{}} \\ S2S1sin2ε & = \frac{_{}}{_{S3S0}} \end{array}$

После измерения параметров Стокса форма эллипса полностью определяется предшествующими уравнениями.

Двумерная сфера Пуанкаре может помочь визуализировать состояние поляризованной волны. Любая точка на или в сфере представляет состояние поляризации, определяемое четырьмя параметрами Стокса, _S0, _S1, _S2 и _S3. На сфере Пуанкаре угол от _S1-S2 плоскости до точки на сфере в два раза больше угла эллиптичности, Угол от оси _S1- до проекции точки в плоскость _S1-S2 в два раза больше угла наклона,

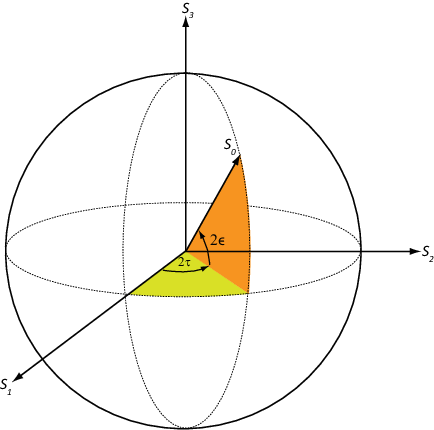
В качестве примера, решите для параметров Стокса поле RHCP, fv=[1,-i], с использованием stokes функция.

S = stokes(fv)

Источники поляризованных полей

Антенны соединены между собой, распространяя электромагнитное излучение на электрические токи в проводах, электромагнитные поля в волноводах или апертурные поля. Эта связь является явлением, общим как для передающих, так и для приемных антенн. Для некоторых передающих антенн токи источника в проводе создают электромагнитные волны, несущие энергию во всех направлениях. Иногда антенна обеспечивает средство для управляемой электромагнитной волны на линии передачи для перехода к волнам свободного пространства, таким как волновод, питающий антенны тарелки. Для приема антенн электромагнитные поля могут индуцировать токи в проводах для генерирования сигналов, которые затем усиливаются и передаются на детектор.

Для передающих антенн форма антенны выбирается для увеличения мощности, проецируемой в заданном направлении. Для приемных антенн выбирается форма антенны для увеличения мощности, принимаемой с определенного направления. Часто многие передающие антенны или приемные антенны формируются в матрицу. Массивы увеличивают передаваемую мощность для передающей системы или чувствительность для принимающей системы. Они улучшают направленность над одной антенной.

Антенне может быть назначена поляризация. Поляризация передающей антенны - это поляризация ее излучаемой волны в дальнем поле. Поляризация приемной антенны фактически является поляризацией плоской волны с заданного направления, что приводит к максимальной мощности на антенных терминалах. По теореме о взаимности все передающие антенны могут служить приемными антеннами и наоборот.

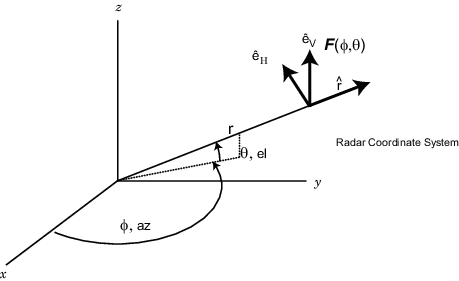
Каждая антенна или решетка имеет ассоциированную локальную декартову систему координат (x, y, z), как показано на следующем рисунке. Дополнительные сведения см. в разделе Глобальные и локальные системы координат. Местная система координат может также быть представлена сферической системой координат, используя азимут, возвышение и координаты диапазона, азимут, el, r, или поочередно писаться, (φ,θ, r), как показано. В каждой точке в дальнем поле можно создать набор единичных сферических базисных векторов $, {\overset{{}{}}_{e} {\overset{}{^}}_{H}, \overset{e}{}$ ^ V, r ^}. Базисные векторы выравниваются соответственно с направлениями ( В дальнем поле электрическое поле ортогонально $\overset{}{}$ единичному вектору r ^. Компоненты поляризованного поля относительно _этого _базиса (EH, EV) называются горизонтальной и вертикальной компонентами поляризованного поля. В радаре принято использовать (H, V) вместо (x, y) для обозначения компонентов поляризованного поля. В дальнем поле поляризованное электрическое поле принимает вид

$E=F (ϕ,θ \frac{)^{}}{} eikrr =_{} (FH ({\overset{}{ϕ}}_{,θ})_{} e^H+FV {\overset{(}{}}_{ϕ} \frac{{,θ}^{)}}{}$ e^V) eikrr

В этом уравнении величина F (start, start) называется векторной диаграммой излучения источника и содержит угловую зависимость поля в области дальнего поля.

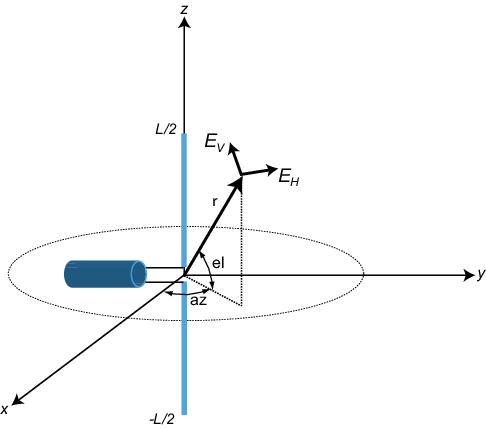
Элемент короткой дипольной антенны

Простейшей поляризованной антенной является дипольная антенна, которая состоит из отрезка провода, соединенного посередине с коаксиальным кабелем. Простейшим диполем, с математической точки зрения, является диполь Герциана, в котором длина проволоки значительно короче длины волны. На следующем рисунке показана схема короткой дипольной антенны длиной L. Эта антенна питается коаксиальным источником питания, разделяющимся на два провода одинаковой длины длиной L/2. Ток I перемещается вдоль оси Z и считается одинаковым во всех точках провода.

Электрическое поле в дальнем поле имеет вид

$\begin{array}{l} _{Er} = \\ _{} 0EH \\ _{=} \frac{{0EV}_{} =}{−} \frac{^{}}{iZ0IL2λcosel} \end{array}$ e − ikrr

В следующем примере вычисляются компоненты вертикальной и горизонтальной поляризации поля. Вертикальная составляющая является функцией угла возвышения и является осесимметричной. Горизонтальный компонент исчезает везде.

Панель инструментов позволяет моделировать короткую дипольную антенну с помощью phased.ShortDipoleAntennaElement object™ системы.

Компоненты поляризации с коротким диполем

Открыть сценарий в реальном времени

Вычислите вертикальную и горизонтальную поляризационные компоненты поля, создаваемого короткодипольной антенной, направленной вдоль z-направления. Постройте график компонентов в зависимости от угла возвышения от 0 ° до 360 °.

Примечание.Этот пример выполняется только в R2016b или более поздних версиях. При использовании более ранней версии замените каждый вызов функции эквивалентным step синтаксис. Например, заменить myObject(x) с step(myObject,x).

Создать phased.ShortDipoleAntennaElement object™ системы.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[1,2]*1e9,'AxisDirection','Z');

Вычислите ответ антенны. Потому что аргумент угла возвышения для antenna ограничивается ± 90 °, вычисляют отклики для азимута 0 ° и затем для азимута 180 °. Объединение двух ответов на графике. Рабочая частота антенны - 1,5 ГГц.

el = [-90:90];
az = zeros(size(el));
fc = 1.5e9;
resp = antenna(fc,[az;el]);
az = 180.0*ones(size(el));
resp1 = antenna(fc,[az;el]);

Наложение ответов на том же рисунке.

figure(1)
subplot(121)
polar(el*pi/180.0,abs(resp.V.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.V.'),'b')
str = sprintf('%s\n%s','Vertical Polarization','vs Elevation Angle');
title(str)
hold off
subplot(122)
polar(el*pi/180.0,abs(resp.H.'),'b')
hold on
polar((el+180)*pi/180.0,abs(resp1.H.'),'b')
str = sprintf('%s\n%s','Horizontal Polarization','vs Elevation Angle');
title(str)
hold off

График показывает, что горизонтальный компонент исчезает, как и ожидалось.

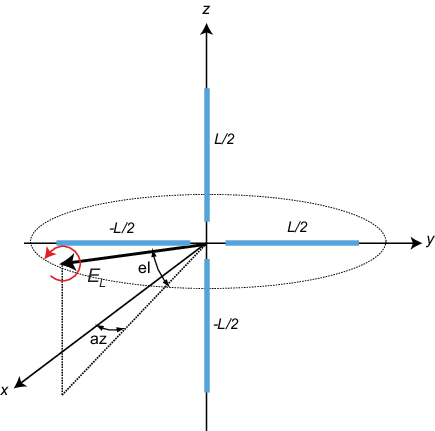
Элемент антенны с перекрещенным диполем

Для генерации кругового поляризованного излучения можно использовать кросс-дипольную антенну. Пересеченная дипольная антенна состоит из двух одинаковых, но ортогональных короткодипольных антенн, которые фазированы на расстоянии 90 ° друг от друга. На следующем рисунке показана схема пересеченной дипольной антенны. Электрическое поле, создаваемое пересеченной дипольной антенной, выполненной из y-направленного короткого диполя и z-направленного короткого диполя, имеет вид

$\begin{array}{l} _{Er} = \\ _{} 0EH \frac{=_{} -}{} \frac{^{iZ0IL2λcosaz}}{e} \\ _{-} \frac{_{}}{ikrEV} = iZ0IL2λ (sinelsinaz \frac{^{+}}{} \end{array}$ icosel) e − ikrr

Коэффициент поляризации _EV/EH, при оценке вдоль оси х, равен всего -i, что означает, что поляризация является точно RHCP вдоль оси х. Это преимущественно RHCP, когда точка наблюдения находится близко к оси х. Удаляясь от оси x, поле становится смесью поляризаций LHCP и RHCP. Вдоль оси -x поле поляризовано LHCP. На рисунке для точки около точки x показано, что поле является главным образом RHCP.

Панель инструментов позволяет моделировать пересеченную дипольную антенну с помощью phased.CrossedDipoleAntennaElement Системный объект.

Компоненты поляризации LHCP и RHCP

Открыть сценарий в реальном времени

В этом примере показана правая и левая компоненты круговой поляризации полей, генерируемых пересекающейся дипольной антенной, с частотой 1,5 ГГц. Видно, как круговая поляризация изменяется от чистого RHCP при угле азимута 0 градусов к чистому LHCP при угле азимута 180 градусов, оба при угле возвышения 0 градусов.

Создать phased.CrossedDipoleAntennaElement объект.

fc = 1.5e9;
antenna = phased.CrossedDipoleAntennaElement('FrequencyRange',[1,2]*1e9);

Вычислите левосторонние и правосторонние компоненты круговой поляризации на основе отклика антенны.

az = [-180:180];
el = zeros(size(az));
resp = antenna(fc,[az;el]);
cfv = pol2circpol([resp.H.';resp.V.']);
clhp = cfv(1,:);
crhp = cfv(2,:);

Постройте график обоих компонентов круговой поляризации на отметке 0 градусов.

polar(az*pi/180.0,abs(clhp))
hold on
polar(az*pi/180.0,abs(crhp))
title('LHCP and RHCP vs Azimuth Angle')
legend('LHCP','RHCP')
hold off

Массивы, поддерживающие поляризацию

Можно создать поляризованные поля из массивов, используя поляризованные антенные элементы в качестве значения Elements свойство объекта System массива. Все массивы Phased Array System Toolbox поддерживают поляризацию.

Матрица поперечного сечения рассеяния

После создания поляризованного поля антенной системой поле излучается в область дальнего поля. Когда поле распространяется в свободное пространство, поляризационные свойства остаются неизменными до тех пор, пока поле не взаимодействует с материальным веществом, которое рассеивает поле во многих направлениях. В таких ситуациях амплитуда и поляризация рассеянной волны могут отличаться от поляризации падающей волны. Поляризация рассеянной волны может зависеть от направления, в котором наблюдается рассеянная волна. Точный способ изменения поляризации зависит от свойств объекта рассеяния. Величина, описывающая отклик объекта на падающее поле, называется матрицей радиолокационного рассеяния (RSCM), S. Измерить матрицу рассеяния можно следующим образом. Когда единичная амплитуда горизонтально поляризованной волны рассеивается, получают как горизонтальную, так и вертикальную рассеянную составляющую. Вызовите эти два компонента _SHH и _SVH. Эти компоненты представляют собой комплексные числа, содержащие изменения амплитуды и фазы падающей волны. Аналогично, когда единичная амплитуда вертикально поляризованной волны рассеивается, получаемая горизонтальная и вертикальная рассеянная составляющая является _SHV и _SVV. Поскольку любое поле инцидента может быть разложено на горизонтальные и вертикальные компоненты, можно упорядочить эти величины в матрицу и записать рассеянное поле в терминах поля инцидента.

$[\begin{matrix} _{EH}^{(scat} \\ )_{}^{EV (} \end{matrix} scat \sqrt{\frac{)]}{^{=}}} \begin{matrix} _{} & {4serverλ 2}_{[} \\ _{} & _{} \end{matrix} \begin{matrix} _{}^{SHHSVHVSVV] [} \\ _{EH}^{(inc} \end{matrix}) \sqrt{\frac{EV}{^{(}}} inc) \begin{matrix} ]_{}^{=} \\ {4serverλ 2}_{}^{[S] [} \end{matrix}$ EH (inc) EV (inc)]

В общем случае матрица поперечного сечения рассеяния зависит от углов, которые создают падающие и рассеянные поля с объектом. Когда падающее поле рассеивается обратно к передающей антенне или обратно, матрица рассеяния симметрична.

Поляризационная сигнатура

Чтобы понять, как рассеянная волна зависит от поляризации падающей волны, необходимо изучить все возможные поляризации рассеянного поля для каждой падающей поляризации. Поскольку этот объем данных трудно визуализировать, рассмотрим два случая:

Для случая кополяризации рассеянная поляризация имеет ту же поляризацию, что и падающее поле.
Для случая перекрестной поляризации рассеянная поляризация имеет ортогональную поляризацию к падающему полю.

Можно представить инцидентные поляризации в терминах угловой пары угол наклона-эллиптичность $(start, start$ ). Каждый единичный вектор поляризации инцидента может быть выражен как

$[\begin{matrix} _{EH}^{(inc} \\ )_{}^{EV (} \end{matrix} inc) \begin{matrix} ] = & [cosun− \end{matrix} \begin{matrix} sinü sinstartcos \end{matrix}$

в то время как вектор ортогональной поляризации равен

$[\begin{matrix} _{EH}^{(inc)} \\ _{}^{⊥EV (} \end{matrix} inc) \begin{matrix} \end{matrix} \begin{matrix} ⊥]=[−sinτ−cosτcosτ−sinτ] \\ [cosun− \end{matrix}$ jsin

Когда у вас есть матрица RSCM, S, сформировать сигнатуру кополяризации путем вычисления

$P^{(co}) {\begin{matrix} =_{}^{[EH (} & _{}^{inc) EV} \end{matrix}}^{(} \begin{matrix} {inc}_{)}^{] * S} \\ _{[}^{EH (} \end{matrix}$ inc) EV (inc)]

где []* обозначает комплексное сопряжение. Для получения сигнатуры кросс-поляризации вычислите

$P^{(кросс}) {\begin{matrix} =_{}^{[EH (} & _{inc}^{) ⊥EV} \end{matrix} (}^{} inc \begin{matrix} )_{}^{⊥] *} \\ S_{}^{[EH (} \end{matrix}$ inc) EV (inc)]

Можно вычислить как сигнатуры кополяризации, так и сигнатуры перекрестной поляризации, используя polsignature функция. Эта функция возвращает абсолютное значение рассеянной мощности (нормализованное на ее максимальное значение). В следующем примере показано, как построить график сигнатур поляризации для матрицы RSCM

$S = \begin{matrix} [ & \frac{}{} \\ \frac{}{} \end{matrix}$ 2i1212i]

для всех возможных поляризаций инцидентов. Диапазон значений угла эллиптичности и наклона охватывает весь возможный диапазон поляризаций.

Печать сигнатур поляризации

Открыть сценарий в реальном времени

Постройте график кополяризации и кросс-поляризации матрицы рассеяния

$[\begin{array}{cc} 2i0.50.5-i \end{array}].$

Укажите матрицу рассеяния. и укажите диапазон углов эллиптичности и углов ориентации (наклона), которые определяют состояния поляризации. Эти углы охватывают все возможные состояния поляризации падающего излучения.

rscmat = [1i*2,0.5;0.5,-1i];
el = [-45:45];
tilt = [-90:90];

Постройте график кополяризации для всех поляризаций инцидентов.

polsignature(rscmat,'c',el,tilt)

Figure contains an axes. The axes with title Co-Pol Response contains an object of type surface.

Постройте график сигнатур перекрестной поляризации для всех поляризаций инцидентов.

polsignature(rscmat,'x',el,tilt)

Figure contains an axes. The axes with title Cross-Pol Response contains an object of type surface.

Потери поляризации из-за несоответствия поля и приемника

Антенна, которая используется для приема поляризованных электромагнитных волн, достигает своей максимальной выходной мощности, когда поляризация антенны согласована с поляризацией падающего электромагнитного поля. В противном случае происходит потеря поляризации:

Потери поляризации вычисляются из проекции (или скалярного произведения) вектора электрического поля передаваемого поля на вектор поляризации приемника.
Потеря возникает, когда существует несоответствие в направлении двух векторов, а не в их величинах.
Коэффициент потерь поляризации описывает долю падающей мощности, которая имеет правильную поляризацию для приема.

Используя сферическую основу передатчика в положении приемника, можно представить падающее электрическое поле (_EiH, _EiV) по

$E =_{} {\overset{}{}}_{EiHe}^_{H} {\overset{+}{}}_{}_{} {EiVe}_{}$ ^ V = EmPi

Вектор поляризации приемника (_PH, _PV) можно представить в локальной сферической основе приемника следующим образом:

$_{} {\overset{}{}}^{}_{}_{} {\overset{}{}}^{}_{P=PHe^′H+PVe^′V}$

На следующем рисунке показана конструкция сферических базисных векторов передатчика и приемника.

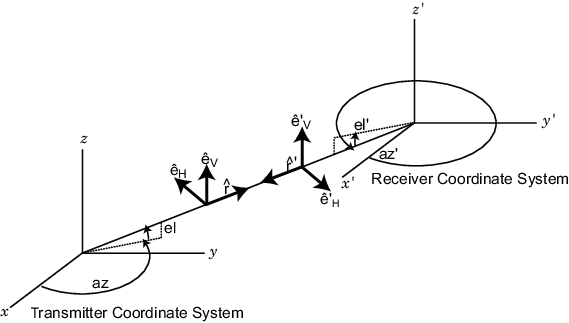
Поляризационные потери определяются:

$\frac{_{}^{}}{_{}^{}^{ρ=|Ei⋅P|2|Ei|2|P|2}}$

и варьируется от 0 до 1. Поскольку векторы определены относительно различных систем координат, для формирования проекции их необходимо преобразовать в глобальную систему координат. Функция панели инструментов polloss вычисляет несоответствие поляризации между падающим полем и поляризованной антенной.

Для достижения максимальной выходной мощности от приемной антенны согласованный вектор поляризации антенны должен быть комплексным сопряжением вектора поляризации входящего поля. В качестве примера, если входящим полем является RHCP, с вектором поляризации, заданным $_{как er} \frac{=}{\sqrt{}} 12_{} ({ex}_{} -$ iey), оптимальной поляризацией антенны приемника является LHCP. Введение комплексного конъюгата необходимо, поскольку поляризации поля описаны в отношении его направления распространения, тогда как поляризация приемной антенны обычно задается в терминах направления распространения к антенне. Комплексный конъюгат корректирует противоположное чувство поляризации при приёме.

Например, если передающая антенна передает поле RHCP, коэффициенты потерь поляризации для различных принятых поляризаций антенны являются

Поляризация приемной антенны	Вектор поляризации приемной антенны	Коэффициент потерь поляризации	Коэффициент потерь поляризации (дБ)
Горизонтальная линейная	а	1/2	3 дБ
Вертикальная линейная	eV	1/2	3
RHCP	$_{er} \frac{=}{\sqrt{}} 12_{} ({ex}_{} -$ iey)	0	∞
LHCP	$_{el} \frac{=}{\sqrt{}} 12_{} ({ex}_{} +$ iey)	1	0

Модель радара, передающего поляризованное излучение

Открыть сценарий в реальном времени

В этом примере моделируется радар слежения на основе однородной прямоугольной матрицы (URA) 31 на 31 (961 элемент). РЛС предназначена для слежения за движущейся целью. В каждый момент времени РЛС указывает в известном направлении цели. Основными требованиями к РЛС являются вероятность обнаружения, pd, вероятность ложной тревоги, pfa, максимальный однозначный диапазон, max_rangeи разрешение диапазона, range_res, (все единицы измерения расстояния в метрах). range_gate параметр ограничивает область, представляющую интерес, диапазоном, меньшим максимального диапазона. Рабочая частота устанавливается в fc. Моделирование длится для numpulses импульсы.

Определение радара

Настройте рабочие параметры РЛС. Существующая конструкция РЛС отвечает следующим техническим условиям.

pd = 0.9;            % Probability of detection
pfa = 1e-6;          % Probability of false alarm
max_range = 1500*1000; % Maximum unambiguous range
range_res = 50.0;    % Range resolution
rangegate = 5*1000;  % Assume all objects are in this range
numpulses = 200;     % Number of pulses to integrate
fc = 8e9;            % Center frequency of pulse
c = physconst('LightSpeed');
tmax = 2*rangegate/c; % Time of  echo from object at rangegate

Интервал повторения импульсов

Установите интервал повторения импульсов, PRIи частота повторения импульсов, PRF, на основе максимального однозначного диапазона.

PRI = 2*max_range/c;
PRF = 1/PRI;

Передаваемый сигнал

Настройка передаваемого прямоугольного сигнала с помощью phased.RectangularWaveform Системный объект (TM). Длительность импульса формы сигнала ,pulse_widthи полоса пропускания импульсов, pulse_bw, определяются выбранным разрешением диапазона, range_res. Укажите частоту выборки, fs, чтобы в два раза превышать полосу пропускания импульсов. Частота дискретизации должна быть кратна целому числу PRF. Поэтому измените частоту выборки в соответствии с этим требованием.

pulse_bw = c/(2*range_res);    % Pulse bandwidth
pulse_width = 1/pulse_bw;               % Pulse width
fs = 2*pulse_bw;                        % Sampling rate
n = ceil(fs/PRF);
fs = n*PRF;
waveform = phased.RectangularWaveform('PulseWidth',pulse_width,'PRF',PRF,...
    'SampleRate',fs);

Антенны и массив URA

Решетка состоит из короткодипольных антенных элементов. Используйте phased.ShortDipoleAntennaElement Объект системы для создания короткодипольной антенны, ориентированной вдоль оси Z.

antenna = phased.ShortDipoleAntennaElement(...
    'FrequencyRange',[5e9,10e9],'AxisDirection','Z');

Определите однородный прямоугольный массив Тейлора с конусом 31 на 31, используя phased.URA Системный объект. Задайте размер массива, используя количество строк, numRowsи количество столбцов, numCols. Расстояние между элементами, d, немного меньше половины длины волны, lambda. Вычислите конусность массива, tw, используя отдельные окна Тейлора для направления строки и столбца. Получение весов Тейлора с помощью taylorwin функция. Постройте график отклика массива 3-D с помощью массива pattern способ.

numCols = 31;
numRows = 31;
lambda = c/fc;
d = 0.9*lambda/2; % Nominal spacing
wc = taylorwin(numCols);
wr = taylorwin(numRows);
tw = wr*wc';
array = phased.URA('Element',antenna,'Size',[numCols,numRows],...
    'ElementSpacing',[d,d],'Taper',tw);
pattern(array,fc,-180:180,-90:90,'CoordinateSystem','polar','Type','powerdb',...
    'Polarization','V');

Движение радиолокационной платформы

Затем задайте положение и движение радиолокационной платформы в phased.Platform Системный объект. Предполагается, что радар неподвижен и расположен в начале координат. Установите Velocity свойство для [0,0,0] и InitialPosition свойство для [0,0,0]. Установите InitialOrientationAxes свойство к единичной матрице для выравнивания координатных осей радиолокационной платформы с глобальной системой координат.

radarPlatformAxes = [1 0 0;0 1 0;0 0 1];
radarplatform = phased.Platform('InitialPosition',[0;0;0],...
    'Velocity',[0;0;0],'OrientationAxes',radarPlatformAxes);

Передатчики и приемники

В РЛС сигнал распространяется в виде электромагнитной волны. Сигнал излучается и собирается антеннами, используемыми в радиолокационной системе. Связать массив с объектом системы радиатора, phased.Radiatorи два коллектора System objects, phased.Collector. Установите WeightsInputPort свойство радиатора true обеспечение возможности динамического управления передаваемым сигналом при каждом выполнении излучателя. Создание двух коллекторов позволяет собирать компоненты горизонтальной и вертикальной поляризации.

radiator = phased.Radiator('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'CombineRadiatedSignals',true,...
    'Polarization','Combined','WeightsInputPort',true);
collector1 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);
collector2 = phased.Collector('Sensor',array,'OperatingFrequency',fc,...
    'PropagationSpeed',c,'Wavefront','Plane','Polarization','Combined',...
    'WeightsInputPort',false);

Оцените пиковую мощность, необходимую в phased.Transmitter Системный объект для вычисления требуемых уровней мощности излучения. Передаваемая пиковая мощность - это мощность, необходимая для достижения минимального SNR обнаружения, snr_min. Минимальный SNR можно определить по вероятности обнаружения, | pd |, и вероятности ложного аварийного сигнала,pfa, с использованием albersheim функция. Затем вычислите пиковую мощность, peak_power, из уравнения радара. Пиковая мощность зависит от общего усиления сигнала, которое является суммой усиления передающего элемента, TransmitterGain и усиление массива, AG. Пиковая мощность также зависит от максимального диапазона обнаружения, rangegate. Наконец, необходимо указать целевое значение поперечного сечения. tgt_rcs. Скалярное сечение радара используется в этом кодовом сечении в качестве аппроксимации, даже если при вычислении полной поляризации позже используется матрица рассеяния сечения радара 2 на 2.

Используя формулу радиолокационного уравнения, оцените общую передаваемую мощность для достижения требуемого SNR обнаружения с использованием всех импульсов.

SNR имеет вклад от усиления передающего элемента, а также усиления матрицы. Вычислите сначала оценку усиления матрицы, затем добавьте усиление матрицы к усилению передатчика, чтобы получить пиковую мощность, которая достигает требуемого SNR.

Используйте приблизительное целевое сечение 1,0 для уравнения радара, даже если анализ требует полной матрицы рассеяния.
Установите максимальный диапазон равным значению «rangegate», поскольку цели за пределами этого диапазона не представляют интереса.
Вычислите коэффициент усиления массива как 10 * log10 (количество элементов)
Предположим, что каждый элемент имеет коэффициент усиления 20 дБ.

snr_min = albersheim(pd, pfa, numpulses);
AG = 10*log10(numCols*numRows);
tgt_rcs = 1;
TransmitterGain = 20;
tau = waveform.PulseWidth;
Ts = 290;
dbterm = db2pow(snr_min - 2*TransmitterGain + AG);
peak_power = (4*pi)^3*physconst('Boltzmann')*Ts/tau/tgt_rcs/lambda^2*rangegate^4*dbterm

peak_power = 5.1778e+05

transmitter = phased.Transmitter('PeakPower',peak_power,'Gain',TransmitterGain,...
    'LossFactor',0,'InUseOutputPort',true,'CoherentOnTransmit',true);

Определить цель

Мы хотим смоделировать возврат импульса от цели, которая вращается так, чтобы матрица поперечного сечения рассеяния менялась от импульса к импульсу. Создание вращающегося целевого объекта и движущейся целевой платформы. Затем вращающаяся мишень представляется в виде зависящей от угла матрицы рассеяния. Поворот в градусах в секунду.

targetSpeed = 1000;
targetVec = [-1;1;0]/sqrt(2);
target = phased.RadarTarget('EnablePolarization',true,...
    'Mode','Monostatic','ScatteringMatrixSource','Input port',...
    'OperatingFrequency',fc);
targetPlatformAxes = [1 0 0;0 1 0;0 0 1];
targetRotRate = 45;
targetplatform = phased.Platform('InitialPosition',[3500.0; 0; 0],...
    'Velocity', targetSpeed*targetVec);

Другие системные объекты

Вектор рулевого управления, определяемый phased.SteeringVector Системный объект.
Формирователь луча, определяемый phased.PhaseShiftBeamformer Системный объект. DirectionSource свойство имеет значение 'Input Port' чтобы дать возможность формирователю луча всегда указывать на известное целевое направление при каждом выполнении.
Распространитель свободного пространства с помощью phased.FreeSpace Системный объект.
Модель предварительного изображения приемника с использованием phased.ReceiverPreamp системный объект.

Распространение сигнала

Поскольку отраженные сигналы принимаются матрицей, используйте формирователь луча, указывающий на направление управления, для получения объединенного сигнала.

steeringvector = phased.SteeringVector('SensorArray',array,'PropagationSpeed',c,...
    'IncludeElementResponse',false);
beamformer = phased.PhaseShiftBeamformer('SensorArray',array,...
    'OperatingFrequency',fc,'PropagationSpeed',c,...
    'DirectionSource','Input port');
channel = phased.FreeSpace('SampleRate',fs,...
    'TwoWayPropagation',true,'OperatingFrequency',fc);
% Define a receiver with receiver noise
amplifier = phased.ReceiverPreamp('Gain',20,'LossFactor',0,'NoiseFigure',1,...
    'ReferenceTemperature',290,'SampleRate',fs,'EnableInputPort',true,...
    'PhaseNoiseInputPort',false,'SeedSource','Auto');

Для такой большой PRI и частоты дискретизации будет слишком много выборок на элемент. Это вызовет проблемы с коллектором, имеющим 961 канал. Для обеспечения управляемости количеством образцов установите максимальный диапазон 5 км. Мы знаем, что цель находится в пределах этого диапазона.

Этот набор осей определяет направление локальных осей координат относительно глобальной системы координат. Это ориентация цели.

Цикл обработки

Предварительно распределить массивы для сбора данных, подлежащих печати.

sig_max_V  = zeros(1,numpulses);
sig_max_H  = zeros(1,numpulses);
tm_V = zeros(1,numpulses);
tm_H = zeros(1,numpulses);

После того, как все объекты системы созданы, закольцовывайте количество импульсов для создания отраженных сигналов.

maxsamp = ceil(tmax*fs);
fast_time_grid = (0:(maxsamp-1))/fs;
rotangle = 0.0;
for m = 1:numpulses
    x = waveform(); % Generate pulse
    % Capture only samples within range gated
    x = x(1:maxsamp);
    [s, tx_status] = transmitter(x);   % Create transmitted pulse
    % Move the radar platform and target platform.
    [radarPos,radarVel] = radarplatform(1/PRF);
    [targetPos,targetVel] = targetplatform(1/PRF);    
    % Compute the known target angle
    [targetRng,targetAng] = rangeangle(targetPos,...
        radarPos,...
        radarPlatformAxes);
    % Compute the radar angle with respect to the target axes.
    [radarRng,radarAng] = rangeangle(radarPos,...
        targetPos,...
        targetPlatformAxes);    
    % Calculate the steering vector designed to track the target
    sv = steeringvector(fc,targetAng);
    % Radiate the polarized signal toward the targat
    tsig1 = radiator(s,targetAng,radarPlatformAxes,conj(sv));
    % Compute the two-way propagation loss (4*pi*R/lambda)^2
    tsig2 = channel(tsig1,radarPos,targetPos,radarVel,targetVel);
    % Create a very simple model of a changing scattering matrix
    scatteringMatrix = [cosd(rotangle),0.5*sind(rotangle);...
        0.5*sind(rotangle),cosd(rotangle)];
    rsig1 = target(tsig2,radarAng,targetPlatformAxes,scatteringMatrix);  % Reflect off target
    % Collect the vertical component of the radiation.
    rsig3V = collector1(rsig1,targetAng,radarPlatformAxes);   
    % Collect the horizontal component of the radiation. This
    % second collector is rotated around the x-axis to be more
    % sensitive to horizontal polarization
    rsig3H = collector2(rsig1,targetAng,rotx(90)*radarPlatformAxes);  
    % Add receiver noise to both sets of signals
    rsig4V = amplifier(rsig3V,~(tx_status>0)); % Receive signal
    rsig4H = amplifier(rsig3H,~(tx_status>0)); % Receive signal
    % Beamform the signal
    rsigV = beamformer(rsig4V,targetAng); % Beamforming
    rsigH = beamformer(rsig4H,targetAng); % Beamforming   
    % Find the maximum returns for each pulse and store them in
    % a vector. Store the pulse received time as well.
    [sigmaxV,imaxV] = max(abs(rsigV));
    [sigmaxH,imaxH] = max(abs(rsigH));
    sig_max_V(m) = sigmaxV;
    sig_max_H(m) = sigmaxH;
    tm_V(m) = fast_time_grid(imaxV) + (m-1)*PRI;
    tm_H(m) = fast_time_grid(imaxH) + (m-1)*PRI;
    
    % Update the orientation of the target platform axes
    targetPlatformAxes = ...
        rotx(PRI*targetRotRate)*targetPlatformAxes;
    rotangle = rotangle + PRI*targetRotRate;
end
% Plot the vertical and horizontal polarization for each pulse as a
% function of time.
plot(tm_V,sig_max_V,'.')
hold on
plot(tm_H,sig_max_H,'r.')
hold off
xlabel('Time (sec)')
ylabel('Amplitude')
title('Vertical and Horizontal Polarization Components')
legend('Vertical','Horizontal')
grid on

Figure contains an axes. The axes with title Vertical and Horizontal Polarization Components contains 2 objects of type line. These objects represent Vertical, Horizontal.

Документация