Определение числовой жесткости модели помогает выбрать между использованием неявного или явного решателя с фиксированным шагом для моделирования в реальном времени. Чтобы определить численную жесткость, сначала используйте рабочий процесс подготовки модели в реальном времени для оптимизации скорости и точности модели. Затем смоделируйте модель с помощью явных и неявных решателей с фиксированным шагом. Сравните результаты моделирования, чтобы увидеть поведение решателей. Если модель численно жесткая, явный решатель обычно проявляет небольшие колебания вокруг нужного решения.
Неявные решатели надежнее явных решателей, однако явные решатели быстрее. Для получения надежных результатов при моделировании в реальном времени с помощью численно жесткой модели используйте неявный решатель с фиксированным шагом. Если модель не является жесткой, используйте явный решатель для максимизации скорости моделирования.
В этом примере эталонные результаты получаются путем моделирования пневматической модели с помощью решателя с переменным шагом. Также можно настроить и смоделировать модель с помощью неявного, а затем явного глобального решателя Simulink ® с фиксированным шагом. Затем сравниваются результаты всех трех моделирований, чтобы определить, является ли пневматическая модель численно жесткой.
Для открытия модели в командной строке MATLAB ® введите:
ssc_pneumatic_rts_reference
Сохранить модель как stiffness_model в папку с возможностью записи по пути MATLAB.
Моделирование модели.
Назначьте результаты моделирования новым переменным.
yRef = yout; tRef = tout;
Постройте график результатов моделирования с переменным шагом.
h1 = figure;
plot(tRef,yRef)
h1Leg = legend({'Reference'});
title('Speed')
xlabel('Time (s)')
ylabel('Speed (rpm)')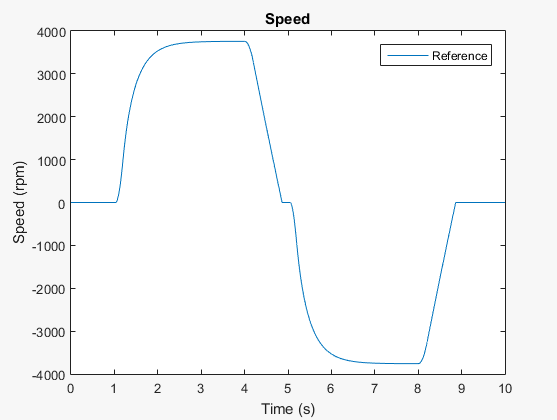
Настройте модель для моделирования с фиксированным шагом с помощью неявного решателя ode14x. На панели Решатель параметров конфигурации задайте:
Введите для Fixed-step
Решатель для ode14x (extrapolation)
В разделе Дополнительные опции (Additional options) Фиксированный размер шага (время основной выборки) до 1e-3
Количество итераций Ньютона для 1.
Нажмите кнопку «Применить».
Моделирование модели.
Назначьте результаты моделирования новым переменным.
yOde14x = yout; tOde14x = tout;
Используйте stairs функция для построения графика результатов неявного моделирования с фиксированным шагом, чтобы можно было увидеть поведение решателя при выполнении каждого шага моделирования.
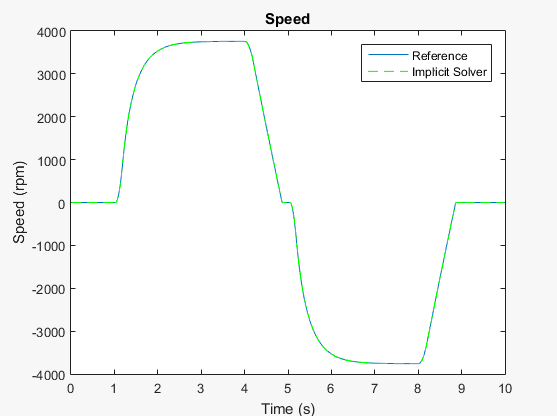
h1 hold on stairs(tOde14x,yOde14x,'g--') h1Leg = legend({'Reference','Implicit Solver'});
Результаты выглядят одинаково.
Настройте модель для моделирования с фиксированным шагом с помощью явного метода решателя с фиксированным шагом mode5. На панели Решатель параметров конфигурации задайте:
Введите для Fixed-step
Решатель для ode5 (Dormand-Prince)
Нажмите кнопку ОК.
Фильтрация входного сигнала для получения требуемой входной производной для явного решателя. В диалоговом окне «PS-S Simulink Converter block» на вкладке «Input Handling» установите для параметра «Filtering and derivatives» значение Filter Input. Нажмите кнопку ОК.
Моделирование модели.
Назначьте результаты моделирования новым переменным.
yOde5 = yout; tOde5 = tout;
Используйте stairs функция для построения графика результатов явного моделирования с фиксированным шагом.
h1 hold on stairs(tOde5,yOde5,'r-') h1Leg = legend({'Reference','Implicit Solver','Explicit Solver'});
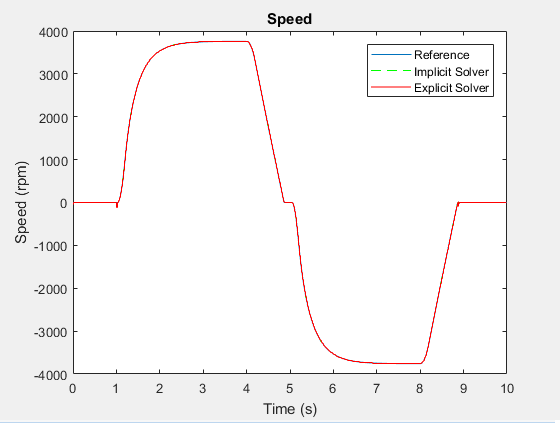
Результаты различаются в точках перегиба.
Чтобы увидеть результаты более точно, увеличьте масштаб до точки перегиба сразу после времени t = ~ 1 сек.
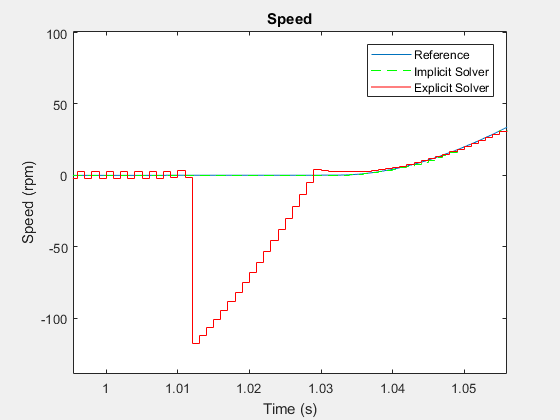
Неявный решатель следует по пути, аналогичному пути, который используется решателем с переменным шагом при создании результатов привязки. Колебания, которые проявляет явный решатель, указывают на то, что модель является численно жесткой. Колебания также указывают на то, что явный решатель является более затратным с точки зрения вычислений, чем неявный решатель для моделирования жесткой модели. Используйте глобальный или локальный неявный решатель с фиксированным шагом для моделирования в реальном времени с численно жесткими моделями, чтобы избежать ненужных вычислительных затрат.