Трехфазная синхронная машина с постоянными магнитами с синусоидальной или трапециевидной обратной электродвижущей силой или пятифазная синхронная машина с постоянными магнитами с синусоидальной обратной электродвижущей силой
Simscape / Электрический / Специализированные Энергосистемы / Электрические Машины
Блок синхронной машины с постоянными магнитами реализует трехфазную или пятифазную синхронную машину с постоянными магнитами. Обмотки статора соединены между собой нитью с внутренней нейтральной точкой.
Трехфазная машина может иметь синусоидальную или трапециевидную обратную форму сигнала ЭДС. Ротор может быть круглым или выраженным для синусоидальной машины. Ротор круглый, когда машина трапециевидная. Предустановленные модели доступны для синусоидальной задней EMF-машины.
Пятифазная машина имеет синусоидальную обратную ЭДС-форму и круглый ротор.
Блок синхронной машины с постоянным магнитом работает в режиме генератора или двигателя. Режим работы диктуется признаком механического крутящего момента (положительный для режима двигателя, отрицательный для режима генератора). Каждая электрическая и механическая часть машины представлена моделью пространства состояния второго порядка.
Синусоидальная модель предполагает, что поток, установленный постоянными магнитами в статоре, является синусоидальным, что подразумевает, что электродвижущие силы являются синусоидальными.
Трапециевидная модель предполагает, что распределение обмоток и поток, установленные постоянными магнитами, создают три трапециевидных задних сигнала ЭДС.
Эти уравнения выражены в опорной системе координат ротора (qd-системе координат). Все величины в системе отсчета ротора относятся к статору.
LqLdpstartmiq
Lq) идиq]
Lq, Ld | индуктивности по осям q и d |
R | Сопротивление обмоток статора |
iq, id | токи по оси q и оси d |
vq, vd | q-осевые и d-осевые напряжения |
ωm | Угловая скорость ротора |
λ | Амплитуда потока, индуцированного постоянными магнитами ротора в фазах статора |
p | Количество пар полюсов |
Те | Электромагнитный момент |
Индуктивности Lq и Ld представляют соотношение между фазовой индуктивностью и положением ротора вследствие солености ротора. Например, индуктивность, измеренная между фазами А и В (когда фаза С остается открытой), определяется следующим образом:
(2
где Starte представляет электрический угол.
На следующем рисунке показано изменение межфазной индуктивности в зависимости от электрического угла ротора.
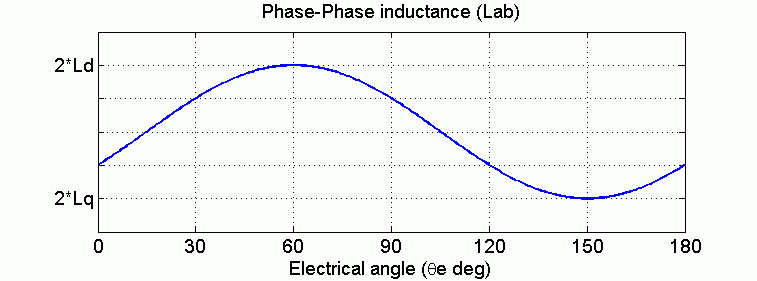
Для круглого ротора изменение фазовой индуктивности отсутствует:
Lab2.
Для явного круглого ротора индуктивности dq задаются следующим образом:
лаборатория) 2
лаборатория) 2
Эти уравнения выражаются в опорной системе координат ротора с помощью расширенного преобразования Park (q1d1 и q2d2). Все величины в системе отсчета ротора относятся к статору.
− λ pobjectmL
5pλ iq1
L | Индуктивность якоря |
R | Сопротивление обмоток статора |
iq1, id1 | токи по осям q1 и d1 |
vq1, vd1 | q1-осевые и d1-осевые напряжения |
iq2, id2 | токи по осям q2 и d2 |
vq2, vd2 | q2-осевые и d2-осевые напряжения |
ωm | Угловая скорость ротора |
λ | Амплитуда потока, индуцированного постоянными магнитами ротора в фазах статора |
p | Количество пар полюсов |
Те | Электромагнитный момент |
Эти уравнения выражаются в фазовом опорном кадре (abc-кадре). Следует отметить, что фазовая индуктивность Ls считается постоянной и не изменяется в зависимости от положения ротора.
ddtib) Te = pλ (Φa′⋅ia+Φb′⋅ib+Φc′⋅ic)
Ls | Индуктивность обмоток статора |
R | Сопротивление обмоток статора |
ia, ib, ic | а, b и с фазные токи |
Фa ', Фb', Фс ' | а, b и c фазоэлектродвижущие силы, в единице измерения амплитуды потока λ |
vab, vbc | ab и bc фазы до фазных напряжений |
ωm | Угловая скорость ротора |
λ | Амплитуда потока, индуцированного постоянными магнитами ротора в фазах статора |
p | Количество пар полюсов |
Те | Электромагнитный момент |
Электродвижущая сила Λ 'представлена:
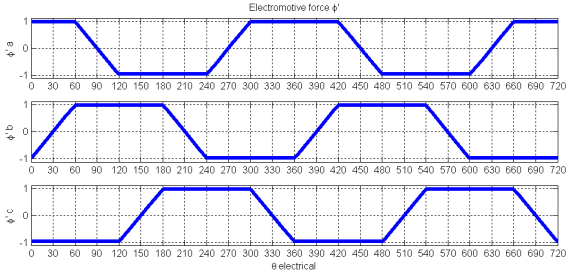
Tm) d
J | Комбинированная инерция ротора и нагрузки |
F | Комбинированное вязкое трение ротора и нагрузки |
θ | Угловое положение ротора |
TM | Механический крутящий момент вала |
Tf | Крутящий момент статического трения вала |
ωm | Угловая скорость ротора (механическая скорость) |
При использовании блоков синхронной машины с постоянным магнитом в дискретных системах может потребоваться использовать малую паразитную резистивную нагрузку, подключенную к клеммам машины, чтобы избежать числовых колебаний. Большие времена выборки требуют больших нагрузок. Минимальная резистивная нагрузка пропорциональна времени выборки. Помните, что с шагом времени 25 мкс в системе с частотой 60 Гц минимальная нагрузка составляет приблизительно 2,5% от номинальной мощности машины. Например, синхронная машина с постоянным магнитом 200 МВА в энергосистеме, дискретизированная с временем выборки 50 мкс, требует приблизительно 5% резистивной нагрузки, или 10 МВт. Если время выборки уменьшено до 20 мкс, достаточна резистивная нагрузка 4 МВт.
Блок синхронной машины постоянного магнита предполагает линейную магнитную цепь без насыщения статора и ротора. Это предположение может быть сделано из-за большого воздушного зазора, обычно встречающегося в синхронных машинах постоянного магнита.
m - Внутренние измерения машиныВектор, содержащий измерительные сигналы. Блок возвращает 13-элементный вектор, если для параметра Число фаз установлено значение 3и 16-элементный вектор, если для параметра Число фаз установлено значение 5. Доступные сигналы зависят от выбранной модели. Демультиплексировать эти сигналы можно с помощью блока выбора шины, предоставленного в библиотеке Simulink ®. Сигналы включают в себя:
Имя | Определение | Единицы | Модель |
|---|---|---|---|
МСФО | Ток статора is_a | A | Все |
ibs | Ток статора is_b | A | Все |
ics | Ток статора is_c | A | Все |
ids | Ток статора is_d | A | Пятифазный синусоидальный |
ies | Ток статора is_e | A | Пятифазный синусоидальный |
IQ | Ток статора is_q | A | Трехфазный синусоидальный |
ids | Ток статора is_d | A | Трехфазный синусоидальный |
iqs1 | Ток статора is_q1 | A | Пятифазный синусоидальный |
ids1 | Ток статора is_d1 | A | Пятифазный синусоидальный |
iqs2 | Ток статора is_q2 | A | Пятифазный синусоидальный |
ids2 | Ток статора is_d2 | A | Пятифазный синусоидальный |
vqs | Напряжение статора Vs_q | V | Трехфазный синусоидальный |
vds | Напряжение статора Vs_d | V | Трехфазный синусоидальный |
vqs1 | Напряжение статора Vs_q1 | V | Пятифазный синусоидальный |
vds1 | Напряжение статора Vs_d1 | V | Пятифазный синусоидальный |
vqs2 | Напряжение статора Vs_q2 | V | Пятифазный синусоидальный |
vds2 | Напряжение статора Vs_d2 | V | Пятифазный синусоидальный |
EA | e_a EMF обратной фазы | V | Трехфазная трапециевидная |
eb | e_b EMF обратной фазы | V | Трехфазная трапециевидная |
ЕС | e_c EMF обратной фазы | V | Трехфазная трапециевидная |
ха | Сигнал эффекта Холла h_a * | логический (0 или 1) | Трехфазный, синусоидальный и трапециевидный |
hb | Сигнал эффекта Холла h_b * | логический (0 или 1) | Трехфазный, синусоидальный и трапециевидный |
hc | Сигнал эффекта Холла h_c * | логический (0 или 1) | Трехфазный, синусоидальный и трапециевидный |
w | Частота вращения ротора wm | рад/с | Все |
тета | Угол ротора тетам | радиус | Все |
Те | Электромагнитный момент Te | N.m | Все |
Сигнал эффекта Холла обеспечивает логическую индикацию обратного позиционирования ЭДС. Этот сигнал очень полезен для непосредственного управления переключателями питания. Изменение состояния происходит при каждом пересечении нуля межфазного напряжения. Эти сигналы должны быть декодированы перед подачей на коммутаторы.
Number of phases - Количество фаз для модели машины3 (по умолчанию) | 5Выберите между трехфазной или пятифазной моделью.
Back EMF waveform - Электродвижущая силаSinusoidal (по умолчанию) | TrapezoidalВыбрать между Sinusoidal и Trapezoidal электродвижущая сила.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3.
Rotor type - Тип ротораRound (по умолчанию) | Salient-poleВыбрать между Salient-pole и Round роторы.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3 и установите форму сигнала EMF назад в Sinusoidal.
Mechanical input - Тип вводаTorque Tm (по умолчанию) | Speed w | Mechanical rotational portВыберите, подается ли на вход крутящий момент, приложенный к валу, скорость ротора или вал машины, представленный Simscape™ вращательным механическим портом.
Выбрать Torque Tm для задания входного момента в N.m и открытия Tm порт. Скорость машины определяется инерцией J машины и разностью между приложенным механическим крутящим моментом Tm и внутренним электромагнитным крутящим моментом Те. Условное обозначение механического крутящего момента - когда скорость положительная. Сигнал положительного крутящего момента указывает режим двигателя, а отрицательный сигнал указывает режим генератора.
Выбрать Speed w чтобы указать скорость ввода в рад/с и открыть w порт. Скорость машины накладывается, а механическая часть модели (Инерция J) игнорируется. Использование скорости в качестве механического ввода позволяет моделировать механическую связь между двумя машинами.
На следующем рисунке показано, как моделировать жесткое соединение вала в двигателе-генераторе, когда крутящий момент трения игнорируется в машине 2. Выход скорости машины 1 (двигатель) соединен с входом скорости машины 2 (генератор), а выход электромагнитного крутящего момента машины 2, Te, приложен к входу механического крутящего момента машины 1, Tm. Коэффициент Kw учитывает единицы скорости обеих машин (pu или рад/с) и передаточное число коробки передач w2/w1. Коэффициент KT учитывает единицы крутящего момента как машин (pu или N.m), так и номинальные параметры машин. Кроме того, поскольку J2 инерции игнорируется в машине 2, J2 добавляется к инерции машины 1, J1.
Выбрать Mechanical rotational port для открытия механического поворотного порта Simscape, позволяющего соединять вал машины с другими блоками Simscape с механическими поворотными портами.
На следующем рисунке показано, как подключить блок источника идеального крутящего момента из библиотеки Simscape к валу машины для представления машины в режиме двигателя или в режиме генератора.
Preset model - Электрические и механические параметры No (по умолчанию) | 01: 0.8 Nm 300 Vdc 3000 RPM - 0.8 Nm | 02: 1.7 Nm 300 Vdc 3750 RPM - 1.7 Nm | ...Заданные электрические и механические параметры для различных номинальных значений синхронного двигателя постоянного магнита крутящего момента (N.m), напряжения шины постоянного тока (V), номинальной частоты вращения (об/мин) и постоянного крутящего момента остановки (N.m).
Выберите одну из стандартных моделей для загрузки соответствующих электрических и механических параметров в записи диалогового окна. Выбрать No (по умолчанию), если вы не хотите использовать предустановленную модель или если вы хотите изменить некоторые параметры предустановленной модели.
Доступны следующие стандартные модели:
No
01: 0.8 Nm 300 Vdc 3000 RPM - 0.8 Nm
02: 1.7 Nm 300 Vdc 3750 RPM - 1.7 Nm
03: 2.8 Nm 300 Vdc 4250 RPM - 3.2 Nm
04: 6 Nm 300 Vdc 4500 RPM - 6 Nm
05: 8 Nm 300 Vdc 2000 RPM - 10 Nm
06: 10 Nm 300 Vdc 2300 RPM - 14.2 Nm
07: 20 Nm 300 Vdc 2200 RPM - 33.9 Nm
08: 24 Nm 300 Vdc 2300 RPM - 41.4 Nm
09: 7.14 Nm 560 Vdc 5000 RPM - 8.3 Nm
10: 7.71 Nm 560 Vdc 5000 RPM - 10.2 Nm
11: 26.13 Nm 560 Vdc 3000 RPM - 27.3 Nm
12: 35.17 Nm 560 Vdc 3000 RPM - 37.4 Nm
13: 42.09 Nm 560 Vdc 3000 RPM - 45.6 Nm
14: 67.27 Nm 560 Vdc 1700 RPM - 70.2 Nm
15: 87.75 Nm 560 Vdc 3000 RPM - 97.96 Nm
16: 111 Nm 560 Vdc 3000 RPM - 126 Nm
При выборе предварительно заданной модели электрические и механические параметры на вкладке Параметры (Parameters) диалогового окна отключаются. Чтобы начать с заданной модели и затем изменить параметры машины, выполните следующие действия.
Выберите предустановленную модель, для которой требуется инициализировать параметры.
Изменить предустановленную модель на No. Параметры машины на вкладке Параметры не изменяются.
Измените параметры машины и нажмите кнопку Применить.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 5или задайте для параметра Количество фаз значение 3 и обратная форма сигнала EMF в Sinusoidal.
Use signal names to identify bus labels - Идентификация с использованием имен сигналов или определения сигналовoff (по умолчанию) | onПри выборе этого параметра выходной сигнал измерения использует имена сигналов для идентификации меток шины. Эта опция используется для приложений, для которых метки сигналов шины должны содержать только буквенно-цифровые символы.
Если флажок снят, на выходе измерения используется определение сигнала для идентификации меток шины. Метки содержат неальфанумерные символы, несовместимые с некоторыми приложениями Simulink.
Stator phase resistance Rs (Ohm) - Фазовое сопротивление статора0.0485 (по умолчанию) | положительный скалярФазовое сопротивление статора Rs (Λ).
Stator phase inductance Ls (H) - Индуктивность статор-фаза-нейтраль8.5e-3 (по умолчанию) | положительный скалярИндуктивность статор-фаза-нейтраль Ls (H) трапециевидной модели.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3 и обратная форма сигнала EMF в Trapezoidal.
Inductances [ Ld(H) Lq(H) ] - Фазно-нейтральные индуктивности[8.5e-3,8.5e-3] (по умолчанию) | двухэлементный векторИндуктивности фаза-нейтраль Ld (H) и Lq (H) в d-оси и q-оси синусоидальной модели с явным полюсным ротором.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3, Обратная форма сигнала EMF в Sinusoidalи тип ротора для Salient-pole.
Armature inductance (H) - Индуктивность якоря синусоидальной модели 0.000395 (по умолчанию) | положительный скалярИндуктивность якоря синусоидальной модели с круглым ротором. Ld равно Lq.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3, Обратная форма сигнала EMF в Sinusoidalи тип ротора для Round.
Specify - Постоянная машинаFlux linkage established by magnets (V.s) (по умолчанию) | Voltage Constant (V_peak L-L / krpm) | Torque Constant (N.m / A_peak)Константа станка для параметризации блока. После выбора константы можно ввести ее значение в соответствующее поле параметра, в то время как два других параметра отключены.
Flux linkage - Постоянный поток0.1194 (по умолчанию) | положительный скалярПостоянный поток λ (Wb) на пары полюсов, индуцированный в обмотках статора магнитами.
Чтобы включить этот параметр, установите для параметра «» Указать «» значение Flux linkage established by magnets (V.s).
Voltage constant - Пиковое напряжение между линиями86.6271 (по умолчанию) | положительный скалярПиковое напряжение между линиями на 1000 об/мин. Это напряжение представляет пиковое напряжение разомкнутой цепи, когда машина приводится в действие как генератор при 1000 об/мин.
Чтобы включить этот параметр, установите для параметра «» Указать «» значение Voltage Constant (V_peak L-L / krpm).
Torque constant - Постоянный крутящий момент на ампер0.7164 (по умолчанию) | положительный скалярКрутящий момент на ампер константы. Эта постоянная предполагает, что машина приводится в действие инвертором, который обеспечивает идеальную синхронизацию между током и обратной ЭДС.
Синусоидальная модель: предполагается синусоидальный ток. Дополнительные сведения см. в разделе ac6_example_simplified.
Трапециевидная модель: Предполагается ток квадратной посуды. Дополнительные сведения см. в разделе ac7_example_simplified.
Чтобы включить этот параметр, установите для параметра «» Указать «» значение Torque Constant (N.m / A_peak).
Back EMF flat area (degrees) - Ширина плоского верха120 (по умолчанию) | положительный скалярШирина плоского верха в течение половины периода электродвижущей силы (градусов) для трапециевидной машины.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3 и обратная форма сигнала EMF в Trapezoidal.
Inertia, viscous damping, pole pairs, static friction [ J(kg.m^2) F(N.m.s) p() Tf(N.m)] - Механические параметры[0.0027 0.0004924 4 0] (по умолчанию) | трехэлементный вектор | четырехэлементный векторКомбинированный коэффициент инерции машины и нагрузки J (kg.m2), комбинированный коэффициент трения вязкости F (N.m.s), пары полюсов p и статическое трение вала Tf (N.m). Если четвертое значение вектора (статическое трение) не указано, блок считает это значение 0.
Чтобы включить этот параметр, установите параметр «Механический ввод» в значение Torque Tm или Mechanical rotational port.
Pole pairs p () - Количество пар полюсов4 (по умолчанию) | положительный скалярКоличество пар полюсов, п.
Чтобы включить этот параметр, установите параметр «Механический ввод» в значение Speed w.
Initial conditions [ wm(rad/s) thetam(deg) ia,ib(A) ] - Исходные условия для трехфазной машины[0,0, 0,0] (по умолчанию) | четырехэлементный векторМеханическая скорость (рад/с), механический угол (в градусах) и мгновенный ток (А) статора для трехфазной машины [wm, Startm, ia, ib].
Так как статор соединен wye, а нейтральная точка изолирована, ток ic в трехфазной машине задается ic = -ia-ib.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 3.
Initial conditions [ wm(rad/s) thetam(deg) ia,ib,ic,id(A) ] - Исходные условия для пятифазной машины[0 0 0 0 0 0] (по умолчанию) | шестиэлементный векторМеханическая скорость (рад/с), механический угол (в градусах) и мгновенный ток статора (А) для пятифазной машины [wm, Startm, ia, ib, ic, id].
Так как статор соединен wye, а нейтральная точка изолирована, то ток в пятифазной машине задается ie = -ia -ib -ic -id.
Чтобы включить этот параметр, задайте для параметра Количество фаз значение 5.
Rotor flux position when theta = 0 - Исходное положение потока ротора90 degrees behind phase A axis (modified Park) (по умолчанию) | Aligned with phase A axis (original Park)Опорное положение потока ротора относительно оси фазы А.
Выбрать 90 degrees behind phase A axis (modified Park) для выбора исходного положения ротора, представленного:
Модифицированное преобразование Park [4] более удобно для векторного управления, поскольку максимальная фазовая индукция происходит при theta = 0.
Выбрать Aligned with phase A axis (original Park) для выбора исходного положения ротора, представленного:
Чтобы включить вкладку Дополнительно (Advanced), установите для параметра Тип моделирования (Simulation type) блока powergui значение Дискретный (Discretic) и на вкладке Настройки (Preferences) снимите флажки Автоматически обрабатывать дискретный решатель (Automatically handle district solver) и Дополнительно (Advanced) для параметра Решатель блоков (Blocks)
Discrete solver model - Метод интеграцииTrapezoidal non iterative (по умолчанию) | Trapezoidal robust | Backward Euler robustМетод интеграции, используемый блоком.
При выборе параметров Автоматически обрабатывать дискретный решатель и Дополнительные настройки решателя блоков в блоке powergui для модели дискретного решателя автоматически устанавливается значение Trapezoidal robust.
Trapezoidal non iterative требуется добавить незначительную шунтирующую нагрузку на клеммы станка для поддержания стабильности моделирования, и моделирование может не сойтись и остановиться при увеличении количества станков в модели.
Trapezoidal robust и Backward Euler robust позволяют исключить необходимость использования паразитных нагрузок. Для исключения топологических ошибок машин, подключенных к индуктивной цепи (например, автоматический выключатель, соединенный последовательно с машиной), машина моделирует ничтожно малую внутреннюю нагрузку 0.01% номинальной мощности.
Trapezoidal robust несколько точнее, чем Backward Euler robust, особенно когда модель моделируется в большее время выборки. Trapezoidal robust может создавать небольшие демпфированные числовые колебания напряжения машины в условиях холостого хода, в то время как Backward Euler robust предотвращает колебания и поддерживает точность.
Дополнительные сведения о том, какой метод следует использовать в приложении, см. в разделе Моделирование дискретизированных электрических систем.
Sample time (-1 for inherited) - Время выборки, используемое блоком-1 (по умолчанию) | скалярВремя выборки, используемое блоком. Чтобы наследовать время выборки, указанное в блоке powergui, установите для этого параметра значение -1 (по умолчанию).
power_brushlessDCmotor пример иллюстрирует использование блока синхронной машины с постоянным магнитом.
[1] Гренье, Д., Л.-А. Дессен, О. Ахриф, Я. Боннасиё, и Б. Лепуфле. «Экспериментальное нелинейное управление крутящим моментом синхронного двигателя постоянного магнита с использованием солености». IEEE ® Transactions on Industrial Electronics, том 44, № 5, октябрь 1997 года , стр. 680-687.
[2] Толият, H.A. «Анализ и моделирование многофазных приводов асинхронных двигателей с переменной скоростью при асимметричных соединениях». Конференция и выставка прикладной электроники, том 2, март 1996 года, стр. 586-592.
[3] Бодарт, Ф., Ф. Лабрике, Э. Матанье, Д. Тельтё и П. Александре. «Управление при нормальной и отказоустойчивой работе многофазных синхронных машин SMPM с механически и магнитно развязанными фазами». Международная конференция по энергетическим, энергетическим и электрическим приводам, март 2009 года, стр. 461-466.
[4] Краузе, П.К., О. Васынчук и С.Д. Судхофф. Анализ электрических машин и приводных систем. IEEE Press, 2002.