Пьезоэлектрическая биморфная балка прямоугольного сечения
Simscape/Электрические/Электромеханические/Мехатронные приводы
Блок Пьезо Бендера моделирует пьезоэлектрический биморфный луч прямоугольного сечения.
Пьезоискатель - пьезоэлектрическое устройство, изгибающееся при приложении электрического потенциала между его пластинами. И наоборот, когда пьезогибатель изгибается, он генерирует электрический потенциал.
Пьезооснователь содержит различные прямоугольные слои пьезоэлектрического материала с поляризацией, перпендикулярной штабелю. Эта поляризация чередуется в каждом слое.
На этом рисунке показана декартова опорная рамка
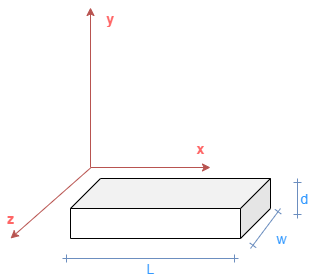
где:
L - длина луча.
w - ширина луча.
d - толщина балки.
Это конститутивные уравнения для пьезоэлектрического материала в составе заряда напряжения,
| [e] TE | (1) |
| (2) |
где:
T - поле напряжения.
[c] - тензор соответствия.
S - поле деформации.
[e] - тензор коэффициента пьезоэлектрического напряжения.
Е - электрическое поле.
D - электрическое поле смещения.
[ϵS] - тензор диэлектрической проницаемости при постоянной или нулевой деформации.
Для моделирования гибкости блок использует уравнения конечных пучков Эйлера-Бернулли. Перемещение и вращение каждого сечения балки в зависимости от оси X определяют кинематику балки.
Этот блок учитывает только силы, приложенные в направлении y, и пьезоэлектрический материал поляризуется для изгиба только в плоскости x-y. По этой причине для описания кинематики необходимо указать только вертикальное смещение в направлении y центра тяжести каждого сечения, y (x) и вращение вокруг оси z каждого сечения, γ z (x).
Из предыдущих предположений, поле деформации в балке Эйлера-Бернулли, подлежащей изгибу, равно:
| ydízdx (x). | (3) |
Поскольку электрическое поле является постоянным между положительной и отрицательной пластинами, vd, блок подставляет уравнение 3 в уравнение 1:
− e31vd.
В этом уравнении E = c11 - модуль Юнга материала, а e31 - (3,1) коэффициент связи пьезоэлектрического напряжения с зарядом, e31Ey.
Это уравнение определяет изгибающий момент из поля напряжения:
e31vdy dS.
Поскольку поляризация материала для d2,0] противоположна поляризации 0, d2], (3,1) коэффициент связи пьезоэлектрического напряжения с зарядом изменяет знак, и изгибающий момент определяется
+ w d e31v,
где 112wd3 - второй момент площади прямоугольного сечения.
В этом уравнении первый член - классическое уравнение луча, подлежащего изгибу, а второй член - электромеханическая связь, обусловленная наличием напряжения на пьезоэлектрическом материале. Это напряжение создает равномерный электрический изгибающий момент, нагруженный вдоль луча.
Блок затем подставляет уравнение 3 в уравнение 2:
) +ϵvd.
Электрический заряд внутри объёма равен интегралу Гаусса электрического смещения:
e31dw díz.
Затем это уравнение определяет заряд, накопленный между двумя секциями луча благодаря пьезоэлектрическому эффекту:
(х1)).
Наконец, с механической точки зрения можно моделировать пьезобелитель как балку Эйлера-Бернулли, нагруженную равномерным крутящим моментом, пропорциональным напряжению:
d e31v
С электрической точки зрения можно моделировать пьезобендер как конденсатор с источником заряда, пропорциональным углу изгиба:
+ϵwldv.
Для дискретизации и решения уравнений Эйлера - Бернулли с пьезоэлектрической муфтой блок Пьезо Бендера использует метод конечных элементов.
Блок дискретизирует пьезогибающую балку в ряд срезов в направлении длины с одинаковой шириной, w и толщиной d. Длина каждого элемента равна общей длине балки, деленной на количество элементов, LNelements.
Эта матрица жесткости конечного элемента балки Эйлера-Бернулли определяет зависимость между вертикальным смещением и углом поворота каждого конца балочного элемента и соответствующими силами и моментами, обусловленными эластичностью балки:
6
Затем для получения уравнений для пьезоэлектрического балочного элемента добавьте члены связи и матрицу масс для инерции:
yCФРRv] = [FCTCFRTRq].
Наконец, это уравнение для пьезоэлектрического балочного элемента с демпфированием:
yCФРRv] = [FCTCFRTRq]
где:
l - длина элемента.
w - ширина элемента.
d - толщина элемента.
112wt3 - второй момент площади.
E - модуль Юнга.
m = αlwd - масса элемента, где "" "" "" "" "" "" "" "" "" "" "" "" "" "
e31 - (3,1) коэффициент связи между пьезоэлектрическим напряжением и зарядом, e31Ey.
λ - электрическая диэлектрическая проницаемость.
bmM - демпфирующая матрица.
bm - коэффициент демпфирования Рэлея, пропорциональный массе.
bk - коэффициент демпфирования Рэлея, пропорциональный жесткости.
6EIl26EIl22EIl − 6EIl24EIl] - матрица конечных элементов жёсткости.
− 3l2 − 22l4l2] - матрица масс.
yC - отклонение вдоль оси Y левого конца элемента.
yR - отклонение вдоль оси Y правого конца элемента.
dwfC - поворот вокруг оси Z левого конца элемента.
αR - поворот вокруг оси Z правого конца элемента.
FC - сила вдоль оси Y левого конца элемента.
FR - сила вдоль оси y правого конца элемента.
TC - крутящий момент в оси Z левого конца элемента.
TR - крутящий момент в оси Z правого конца элемента.
v - напряжение на верхнем и нижнем электродах.
q - аккумулированный заряд между электродами и пьезоэлектрическим материалом.
В спецификации пьезоэлектрического бендера обычно приводятся следующие данные:
Размеры (l, w, d)
Масса, м
Номинальное напряжение, переменное
Свободное отклонение при номинальном напряжении, без
Сила блокировки при номинальном напряжении, Fблок
Емкость, Cpiezo
Первая резонансная частота, f1
Можно рассчитать основные параметры материала пьезоэлектрического бендера, используя параметры таблицы данных.
Во-первых, блок решает отношения напряжение-сила отклонения из установившихся уравнений без приложенного крутящего момента и без зажима конфигурации:
Эти уравнения определяют зависимость между отклонением наконечника, напряжением и силой наконечника:
E w d3=FR4l3Ewd3+v6 e31l2E d2yfree=6l2 d w e31 vrated12EI=6 e31l2 vratedE d2Fblock =−3 d w e31 vrated2l
Блок вычисляет емкость, предполагая, что приложенная нулевая сила:
12e312E) l wd.
Наконец, это уравнение показывает зависимость между плотностью и массой:
.
После определения всех взаимосвязей между фундаментальными параметрами и параметрами таблицы можно вычислить фундаментальные параметры с помощью следующих уравнений:
)
Затем подставьте эти уравнения в конститутивные уравнения:
Можно вычислить первую резонансную частоту свободного от зажима пучка равномерного сечения, используя следующее уравнение:
Затем блок параметризует динамику непосредственно путем задания требуемой собственной частоты.
Балки имеют различные граничные условия на левом и правом концах:
Свободно (Free) - как смещение, так и вращение равны любому значению.
Просто поддерживается - смещение равно 0.
Зажатый - как смещение, так и вращение равны 0.
В этой таблице показаны возможные конфигурации границ для пьезогибающей балки.
| Конфигурация | Модель |
|---|---|
| Без зажима |
|
| Поддерживается-поддерживается |
|
| Зажатый-зажатый |
|
[1] Тадмор, Э. Б. и Г. Коса. «Коррекция электромеханической муфты для пьезоэлектрических многослойных балок». Журнал микроэлектромеханических систем, том 12, № 6, декабрь 2003, стр. 899-906. DOI.org (Crossref), doi:10.1109/JMEMS.2003.820286.
[2] Benjeddou A, Trindade MA, Ohayon R. «Унифицированная балочная модель конечных элементов для удлинительных и сдвиговых пьезоэлектрических исполнительных механизмов». Журнал интеллектуальных материальных систем и структур. 1997;8(12):1012-1025. doi:10.1177/1045389X9700801202
[3] Гэвин, Анри П. «Балочный элемент Stiffness Матрицы». 421L ЦВЕ. Матричный структурный анализ. Университет Дьюка, 2014.
Линейный привод пьезо | Поворотный привод Пьезо | Пьезо-Стек