Контроллер RST

Прогнозирующее управление с использованием полиномиального представления

Библиотека:
Simscape / Электрический / Контроль / Общий Контроль

Описание

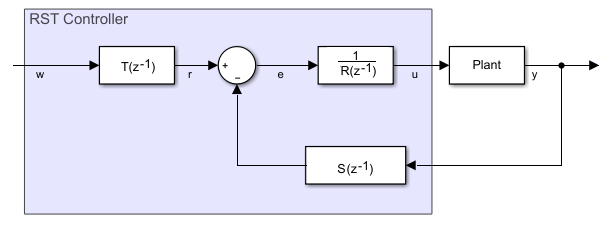
Блок контроллера RST реализует обобщенный прогнозирующий контроллер, используя полиномиальное представление отслеживания опорного сигнала. На схеме показана эквивалентная схема алгоритма управления.

Уравнения

Управляемая авторегрессионная интегрированная модель скользящего среднего (CARIMA) описывает завод:

$A (^{z} - 1) y^{(k}) =^{z} - dB (z \frac{- 1) u^{(} k}{-^{1)}}$ + e (k) C (z − 1) D (z − 1)

$A (^{z} - 1)_{}^{}_{_{}}^{_{}}$ =1+a1z−1+⋯+anAz−nA

$B (^{z} - 1_{)}_{}^{}_{_{}}^{_{}}$ =b0+b1z−1+⋯+bnBz−nB

$C (^{z} - 1$ ) = 1

$D (^{z} - 1)^{=} 1$ − z − 1,

где:

d - время простоя системы.
y (k) - производительность установки.
u (k) - выходной сигнал контроллера.
e (k) - белый шум с нулевым средним значением.
A (^z-1) и B ^(z-1) являются системными многочленами.
_nA и _nB - степени многочленов.
C (^z-1) и D ^(z-1) являются полиномами возмущений для получения ошибки установившегося состояния.

Модель прогнозирования задается как

$\overset{}{y}^(k +_{j 'k)} =^{Gj} - d^{(} z^{- 1)} D (z - \frac{_{1)} z^{-} d -^{1u}}{(k^{+} j}) + Hj \frac{-_{d} (z^{−}}{1)^{D} (} z -$ 1) C (z − 1) u (k − 1) + Fj − d (z − 1) C (z − 1) y (k)

$j \overset{}{= привет,}$ л.с.

где:

Привет - это минимальный прогноз.
hp - горизонт прогнозирования.

Будущая управляющая последовательность, вычисленная в момент времени k, равна

$u (k + j -$ 1 | k),

где

$j \overset{}{= 1,}$ hc пр

и hc - горизонт управления.

Прогнозируемые значения выходного сигнала:

$\overset{}{y}^(k +$ j 'k).

Для определения системных многочленов $_{Fj -} d^{(} z$ − $_{1),}^{Gj} -$ d (z $-_{1)}^{} и$ Hj − d (z − 1) блок использует два диофантовых уравнения. Первое уравнение Диофантина

$\frac{C (^{z} -}{1)^{A} (z^{-} 1})_{D (} z^{-} 1)^{= Ej} \frac{_{- d} (^{z} -}{1)^{+} z -^{j}} +$ dFj − d (z − 1) A (z − 1) D (z − 1),

где:

$_{Ej -} d^{(} z − 1)_{}^{}_{_{}}^{_{}}$ =1+1+e1z−1+⋯+enEz−nE

$_{Fj -} d^{(} z -_{} 1)_{}^{}_{_{}}^{_{}}$ =f0+f1z−1+⋯+fnFz−nF

$_{nE} = j −$ d − 1

$_{nF} = \max_{} (_{nA} +_{nD} - 1,$ nC − j + d)

Второе уравнение Диофантина

$_{Ej -} d^{(} z -^{1)} B (z^{−} 1_{) =} C^{(} z -^{1)}_{Gj -} d^{(} z$ − 1) + z − j + dHj − d (z − 1),

где:

$_{Gj -} d^{(} z -_{} 1)_{}^{}_{_{}}^{_{}}$ =g0+g1z−1+⋯+gnGz−nG

$_{Hj -} d^{(} z -_{} 1)_{}^{}_{_{}}^{_{}}$ =h0+h1z−1+⋯+hnHz−nH

$_{nG} = j −$ d − 1

$_{nH} = \max_{} (_{nC}, nB$ + d) − 1

Результирующая модель прогнозирования

$\overset{}{y}^(k +_{j 'k)} =^{Gj} - d^{(} z^{- 1)} D (z - {\overset{1}{}}_{)} z - d -$ 1u (k + j) + y ^ 0 (k + j' k),

где

${\overset{}{y}}_{^} 0 (k + \frac{_{j 'k)} =^{} Hj -^{d} (}{z -^{1})} D (z - \frac{_{1)} C^{(z}}{- 1^{)} u} (k$ − 1) + Fj − d (z − 1) C (z − 1) y (k)

представляет собой свободный отклик системы.

Используя матричную нотацию, модель прогнозирования может быть записана как

$\overset{}{y}^=_{} {Gud}_{} +$ y ^ 0,

где:

$\overset{}{y}^{\overset{}{=} [y^(k + \overset{}{} hi 'k), y^(k \overset{}{+} hi + 1 |}^{k}$ ), ⋯,y^ (k + hp' k)] T

$G = \begin{matrix} _{} & _{} \\ _{} & _{} & _{} \\ _{} & _{} \\ _{} & _{[ghi−d−1⋯g00⋯0ghi−dg1g00 ghc−1 g0ghp−d−1 ghp−hc−1} \end{matrix}]$

$_{ud} {= [D^{(} z - 1) u (k^{),} ⋯,D (z − 1}^{)}$ u (k + hc − 1)] T

${\overset{}{y}}_{^} {0 {\overset{=}{}}_{} [y^0 (k {\overset{+}{}}_{} hi 'k), y^0 {\overset{k}{(}}_{} + hi + 1}^{|}$ k), ⋯,y^0 (k + hp' k)] T

Чтобы минимизировать ошибки отслеживания и выходные данные контроллера, блок использует функцию затрат. Для компромисса между минимизацией ошибки отслеживания и минимизацией выходного сигнала контроллера блок использует весовой коэффициент λ, такой, что

$J {= (_{} {\overset{}{Gud}}_{+} y}^{^} 0_{-} {\overset{)}{w}}_{} T ({Gud}_{}^{+}_{y}$ ^ 0 − w) + λ udTud

для

$D (^{z} - 1) u (k$ + i) = 0

$i∈[hc,hp−d−1],$

где w - вектор опорной траектории. Минимизация функции затрат дает уравнение для оптимальной последовательности управления:

$_{ud}^{} * =^{} ({GTG}_{+}^{} λ Ihc)_{GT} [$ w − y ^ 0].

Так как _{γ j} и $j \overset{}{= hi,}$ hp β являются элементами в первой строке ${^{матрицы} (_{GTG} +}^{}^{}$ λ Ihc) − 1GT, применение принципа отходящего горизонта дает уравнение алгоритма управления как

$D (^{z} - 1) u_{(k)}^{}_{} =∑j=hihpγj[w ({\overset{}{k}}_{+} j 'k) - y$ ^ 0 (k + j' k)].

Подстановка с использованием ${\overset{}{y}}_{^} 0 (k + \frac{_{j 'k)} =^{} Hj -^{d} (}{z -^{1})} D (z - \frac{_{1)} C^{(z}}{- 1^{)} u} (k$ − 1) + Fj − d (z − 1) C (z − 1) y (k) дает такую форму уравнения алгоритма управления:

$C (^{z} - 1)^{D} (z - 1)_{u (}^{k)}_{}_{}^{}^{=−∑j=hihpγjHj−d} (z - 1)_{D (z}^{-}_{1})_{u} (k^{−} 1)_{}^{}_{} {−∑j=hihpγjFj−d}^{(} z - 1) y$ (k) +∑j=hihpγjC (z − 1) w (k + j).

Полиномиальная форма алгоритма управления выглядит следующим образом:

$R (^{z} - 1) u (k^{)} + S (z -^{1)} y (k) =$ T (z − 1) w (k + hp),

где:

$R (^{z} - 1) =^{(} C (_{z -}^{1)}_{}^{}_{}^{} +\sumj=hihpγjz-1Hj-d^{(z} -$ 1)) D (z − 1),

$S (^{z} - 1_{)}^{}_{}_{}^{=∑j=hihpγjFj−d} ($ z − 1),

$T (^{z} - 1)^{=} C_{(z -}^{1})_{}^{}$ ∑j=hihpγjz−hp+j.

Ограничения

Чтобы получить многочлены R, R и T, используйте дискретное время вместо функции передачи непрерывного времени.

Порты

Вход

развернуть все

`r` - Ссылка на завод
скаляр

Опорный сигнал системы установки.

Типы данных: single | double

`y` - Производительность установки
скаляр

Выходной сигнал системы установки.

Типы данных: single | double

Продукция

развернуть все

`u` - Выход контроллера
скаляр

Выходной сигнал системы управления.

Типы данных: single | double

Параметры

развернуть все

`Controller parameterization` - Метод параметризации
`Controller polynomials` (по умолчанию) | `Generate polynomials`

Способ параметризации контроллера. Если известны дискретные значения полинома R, S и T, выберите Controller polynomials. В противном случае выберите Generate polynomials.

Зависимости

Выбор метода параметризации позволяет использовать другие параметры.

`R polynomial` - полиномиальные значения R
`1` (по умолчанию) | положительный, скалярный или векторный

Вектор многочленов R для управления RST.

Зависимости

Выбор Controller polynomials для параметра Параметризация контроллера включает этот параметр.

`S polynomial` - Полиномиальные значения S
`1` (по умолчанию) | положительный, скалярный или векторный

Вектор S многочленов для управления RST.

Зависимости

Выбор Controller polynomials для параметра Параметризация контроллера включает этот параметр.

`T polynomial` - T многочленов
`1` (по умолчанию) | положительный, скалярный или векторный

Вектор многочленов T для управления RST.

Зависимости

Выбор Controller polynomials для параметра Параметризация контроллера включает этот параметр.

`Model discrete transfer function numerator` - Числитель передаточной функции
`1` (по умолчанию) | скаляр или вектор

Числитель системной дискретизированной передаточной функции. Для определения функции дискретного переноса при наличии лицензии на Toolbox™ системы управления используйте c2d функция.